BGU Physics Department logo

Non-equilibrium steady state of stochastic circuits

Doron Cohen

The study of systems with non-equilibrium steady state (NESS) has become of great interest in recent years. The paradigm for NESS is a system which is coupled to two equilibrated reservoirs "A" and "B" that are characterized by different temperatures \(T_A\) and \(T_B\). The steady state of the system is not canonical. A particular case of special interest is having one reservoirs (call it "A") that is replaced by a stationary driving source, while the relaxation is provided by a bath (call it "B") that has some finite temperature \(T_B\). This is still the same paradigm because formally the driving source "A" can be regarded as a bath that has an infinite temperature \(T_A=\infty\).

 

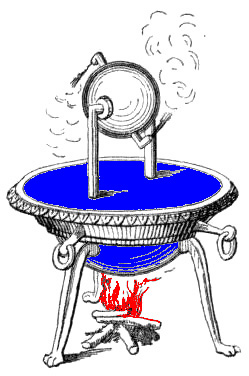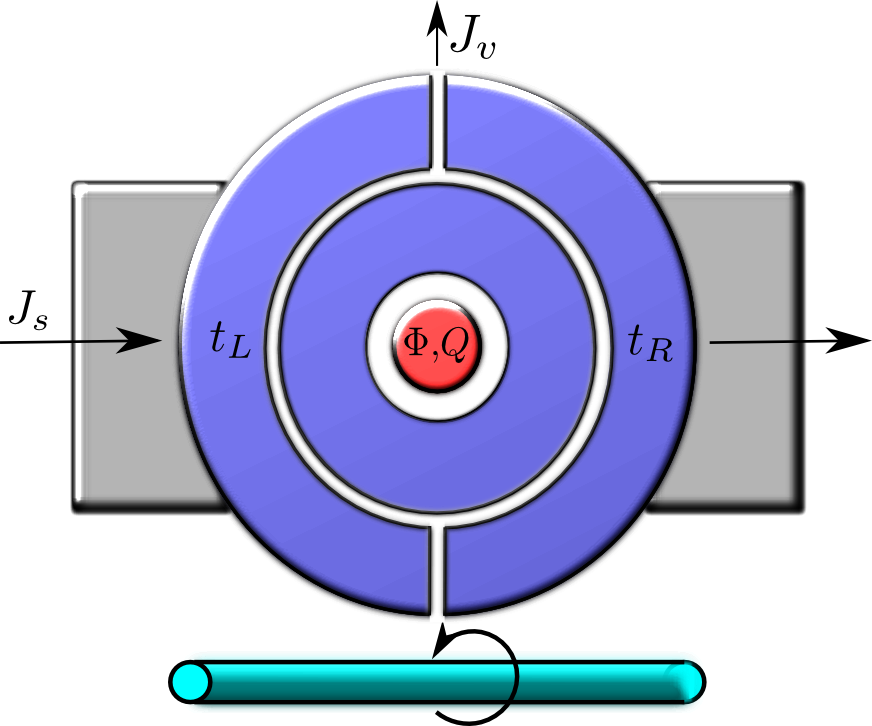
Upper figure: Illustration of a prototype model system: a ring that is made up of N isolated sites with on site energies E_n. The ring is coupled to a heat reservoir (represented by the blue "environment") and subjected to a noisy driving field (represented by the red circle) that induces a current in the ring.

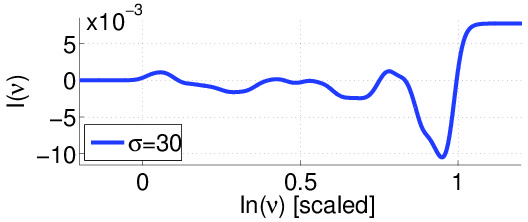
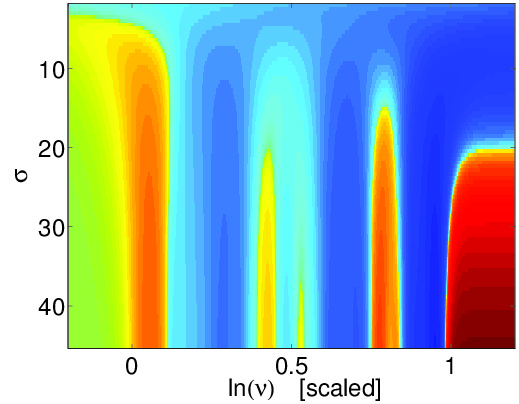
Lower figure: In the upper panel the current in the ring is plotted as a function of the scaled driving intensity. In the lower panel this dependence is imaged for various strengths ("sigma") of disorder (each row corresponds to one plot as above). More generally we have analyzed the statistics of the current over many realizations of the disorder.



 

In subsequent studies we have addressed questions that concern the relaxation of such currents, and how the relaxation depends on percolation and localization properties of the model. Currently we are trying to extend the theory, considering general stochastic active networks.




 

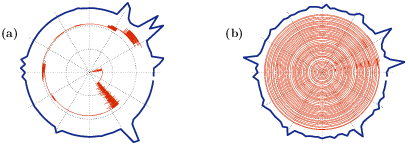
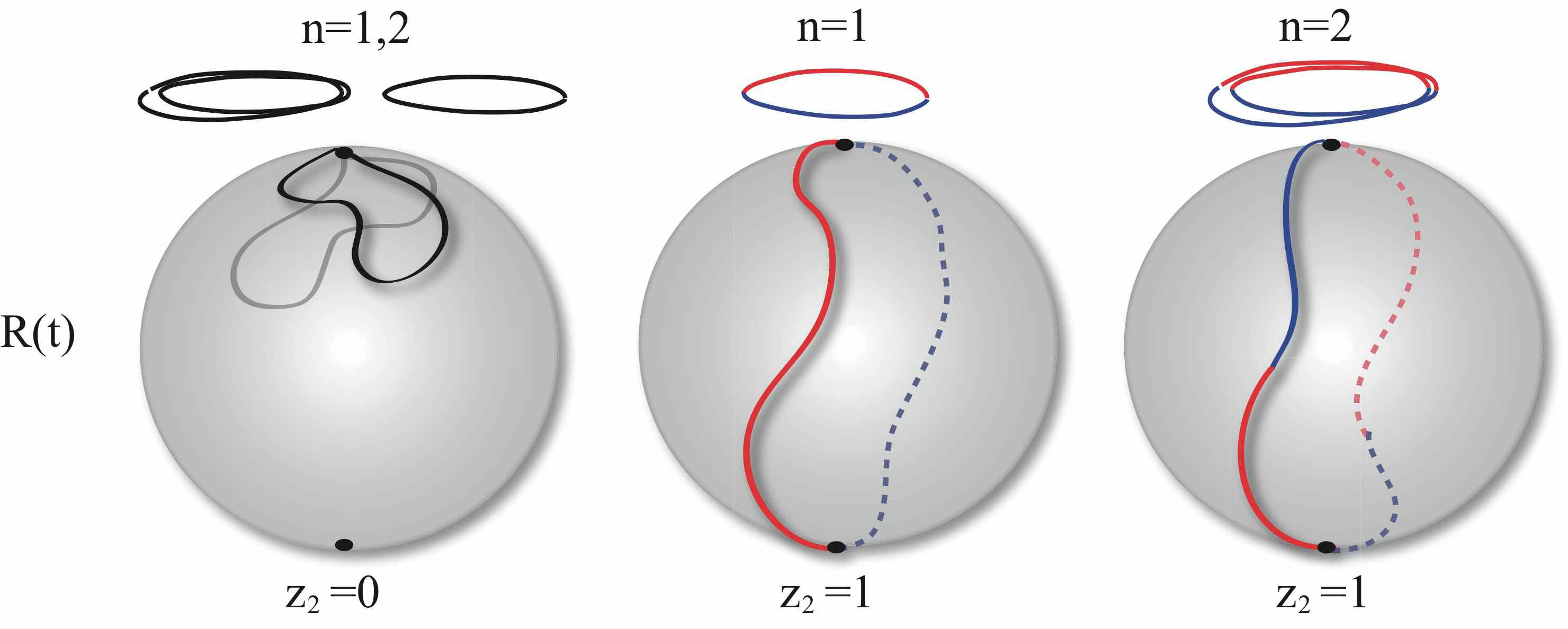
The above figure is taken form our Nature Scientific Report publication entitled "Percolation, sliding, localization and relaxation in topologically closed circuits". The radial direction is time and the angle is the position. (a) For small bias the dynamics is over-damped. (b) For large bias the dynamics is under-damped. The transition has to do with the de-localization of the eigen-modes, and surprisingly happens before the "sliding transition" that had been widely discussed in past literature.

For references click here
For more highlights click here

Phase measurements in quantum mechanics

Amnon Aharony

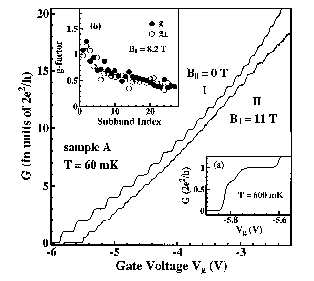
When a wave splits through two slits, one obtains an interference pattern which depends on the phase difference between the two paths. Recently, experiments studied mesoscopic solid state interferometers. A magnetic flux \Phi enclosed between the paths adds a Aharonov-Bohm (AB) phase difference, yielding a current with a term containing \(\cos\left(2\pi e\Phi/hc+\beta\right)\) . The phase shift \(\beta\) was interpreted as the intrinsic phase \(\alpha\) of the quantum transmission via a quantum dot (QD) located on one of the paths. This intrinsic phase is important for studies of the quantum properties of the QD, relevant to many nanoscopic devices. We have shown that in fact, the measured \(\beta\) is usually not equal to αα ; except for very specific conditions (not yet discussed in the textbook chapters on the AB interferometer), the measured phase shift is due to losses of current out of the paths. We have then found theoretical conditions for when \(\beta=\alpha\). We have also given detailed predictions for the conductance of a closed interferometer (with no losses), and shown that the AB oscillations are strongly affected by the finite width of the interferometer's arms (see Fig. 2). Given the complications of the interpretations of such measurements, we have recently proposed an alternative: the quantum noise of the current through a quantum dot was shown to also contain information on the transmission phase.
 

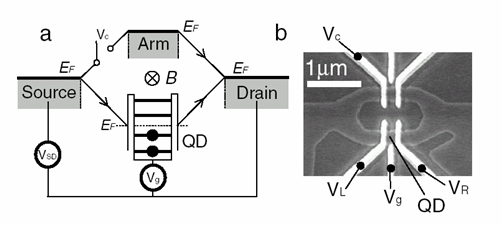Figure 1: electrodes on top of a two-dimensional electron gas, determining the potential seen by the electrons. The quantum dot, which can capture or scatter electrons, is in the center. Figure 2: Right: electrodes in the AB interferometer. Left: schematic picture of the interferometer, with several bound states on the quantum dot, which sits on one arm, and with the magnetic field B in the center.

 

Magnetism and ferroelectricity in rare earth oxides

Amnon Aharony

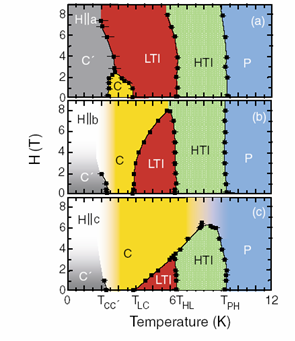
Insulating rare-earth oxides often exhibit rich magnetic phase diagrams, with interesting competing magnetic structures. Often, these phase diagrams are due to structures which are close to cubic or tetragonal. In these highly symmetric structures, the magnetic ground states are highly degenerate, implying magnetic frustration. We have studied several mechanisms which lift the frustration and yield a variety of magnetic ordered states. One mechanism involves quantum fluctuations. The zero point motion associated with these fluctuations creates "order out of disorder", and chooses some ground states over others. The second mechanism involves small magnetic anisotropies, usually due to spin-orbit interactions. Again, these anisotropies lift the degeneracy, and pick specific structures. Examples include several cuprates (the parents of high temperature superconductors) and nickel vanadate, whose structure is close to a planar Kagome lattice. The figure shows the temperature-magnetic field phase diagram of the latter material, which contains various types of (commensurate and incommensurate) magnetic order. Interestingly, this material shows multiferroic behavior: the low temperature incommensurate magnetic phase ("LTI") also exhibits ferroelectric order, which can thus be switched on and off by both a magnetic and an electric field. This has potential applications for spintronics.

Interacting topological phases

Dganit Meidan

 

Topological phases of matter are characterized by a gapped bulk, yet a perfectly conducting surface. The flow on the surface is topologically protected such that it cannot decay even in the presence of defects and imperfections. These insulating phases with perfectly conducting edge states hold promise for a multitude of applications, most prominent of which is the development of new quantum computational schemes that are inherently protected against errors.
When the system is strongly interacting, the emergent surface states may have additional striking properties, such as carry a fraction of the electron charge and obey an exotic exchange statistics. Despite the growing interest in the interplay between interactions and topology, the study of interacting topological phases remains a formidable task. In particular, finding experimental realizations of interacting topological phases, and their signatures in transport measurements, constitutes a vital step towards motivating experimental work.
 

Fig1:In the thin torus limit, a two dimensional system can be mapped onto a one dimensional pump.
Fig2: Three different classes of pumps for systems with a two-fold degenerate ground state and a time-reversal restriction on the pumping cycle: the trivial class, the integer pump, and the fractional pump which pumps a fractional spin without pumping charge.
Fig3:Interacting Majorana fermions at the end of multiple Kitaev chains form emergent many-body end states identified to be a topological Kondo-like resonance.

Topological Superconductors and Majorana Fermions

Eytan Grosfeld

 

Majorana fermions have been ardently sought after in particle physics since their theoretical prediction in the 1930s. Conclusive experimental evidence for their presence is still lacking. Much of the focus has shifted in recent years to condensed matter physics, where Majorana states are expected to form on the edges of topological superconductors and carried by magnetic vortices through the superconductors. The presence of a Majorana state on the vortex core has far reaching consequences for the quantum statistics of the vortex: it increases the degeneracy of the quantum state in such a way that when two vortices are interchanged, the quantum state gets rotated in a non-trivial way. Detection of Majorana states and their induced vortex statistics requires the design of clever methods of probing the system, but the effort is worthwhile: their discovery can open a pathway to novel quantum computation schemes, largely immune to decoherence.
 

Figure 1: A vortex interferometer, sensitive to the quantum statistics of solitons trapping Majorana modes
Figure 2: A vortex line in a quasi-2D geometry supporting Majorana modes on the end points of the vortex line
Figure 3: A topological phase transition for a vortex line - Majorana end states appear in a finite parameter regime

Intracellular networks in bacteria

Yigal Meir

 

Bacteria are constantly sensing their environments and adjusting their behavior accordingly. Signaling occurs through networks of proteins and nucleic acids, culminating in changes of gene expression and so changes in the proteins of the cell. We are focused on the architecture of these intracellular networks. What is the relation between network architecture and function? For example, can we understand the selection of architectures in terms of general information-processing concepts such as signal to noise, memory, and adaptation? Even in a single bacterium such as E. coli, there are hundreds of coexisting networks. Our belief is that a deep study of a small number of "model" networks will yield general tools to analyze information processing by cell. It is important to choose these model networks carefully. The network components should be well characterized and the physiological function of the network should be known and subject to quantitative measurement. Probes of the internal dynamics of the network such as fluorescence resonance energy transfer (FRET) or direct imaging of dynamic spatial structure, will be critical in developing and testing quantitative models. It will also be important to choose networks which complement each other well, spanning a broad range of architectures and functions. A preliminary list includes (i) chemotaxis, which requires adaptation and rapid response to changing chemical concentrations, (ii) cell-division networks, where accuracy and checkpoints are essential, and (iii) metabolic networks which tie together diverse inputs to maintain homeostasis.

cell1.JPG

Solving the "0.7 Anomaly"

Yigal Meir

 

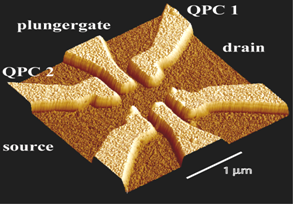
The simplest nanoelectronics device, and the basic building block for more complicated devices, is a "quantum point contact," a constriction connecting large electron reservoirs (see picture on the right). According to quantum mechanics the conductance through such a device should increase as the gap grew bigger by integer steps of universal value. Surprisingly, an additional first step approximately 0.7 times the expected universal value had also been observed, which became known as "the 0.7 anomaly" (see picture on the left). Previously we demonstrated that the phenomenology of this anomaly can be explained by the existence of a magnetic impurity, a localized electron in the quantum-point contact PRL 89, 196802 (2002). Using extensive density-functional calculations we demonstrated impurity.png the emergence of a magnetic impurity at the quantum point contact (see picture on the right) because a lower density of the electrons near the quantum point attracts the other electrons towards it. The wavy nature of such electrons then causes ripples, trapping an electron and causing the 0.7 anomaly.
 

 

Quantum disordered magnets

Moshe Schechter

The interest in magnetism, and specifically quantum magnetism, is twofold. Firstly, magnetic materials are of immense significance for the advance of technology. With reduced size of current and future devices, quantum effects become relevant, and their understanding is crucial to further advance. At the same time, magnetic systems are an ideal tool in the study of various physical phenomena, as they allow the realization of theoretical models with negligible extraneous interactions, and with the ability to tune the relevant parameters.

Perhaps the most studied model for interacting systems is the Ising model. With the addition of a transverse field term and a random field term the model is described by the Hamiltonian

\(H_{Is}=-\sum_{ij}J_{ij}S_i^zS_j^z-\Gamma\sum_iS_i^x-\sum_ih_iS_i^z\)

and allows the study of the interplay of interactions with quantum fluctuations and disorder. This interplay is of much recent interest, as it is essential in phenomena such as the superconducting-insulator transition, the quantum Hall effect, and high superconductivity. Recently we have shown that this model is realized in anisotropic dipolar magnets, allowing its experimental study in new regimes. This both led to an understanding of existing experiments, and motivated new experiments which were recently done and raised new questions regarding the disordering of spin glasses and ferromagnets by random fields. Current questions of interest include the transition between the ferromagnetic and glassy phase as function of disorder, random fields in nano magnetic grains, and entanglement of different degrees of freedom near the quantum phase transition.

Low temperature universality in disordered solids

Moshe Schechter

A large variety of otherwise very different amorphous and disordered solids show, at temperatures lower than 3 Kelvin, remarkable universality in their properties.
Most astounding, the ratio \(\lambda/l\) of the phonon wavelength divided by its mean free path is roughly 1/150, this value being constant in wavelength, temperature, and very similar between otherwise very different materials.
For 4 decades this phenomenon is discussed within the framework of the phenomenological model of tunneling two level systems (TLSs). However, crucial questions such as the nature of the tunneling states, the universality and smallness of the ratio \(\lambda/l\) , and the energy scale dictating the temperature of 3K below which the phenomenon is observed, remain unanswered.

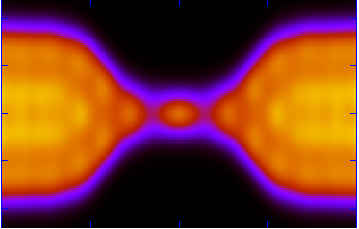
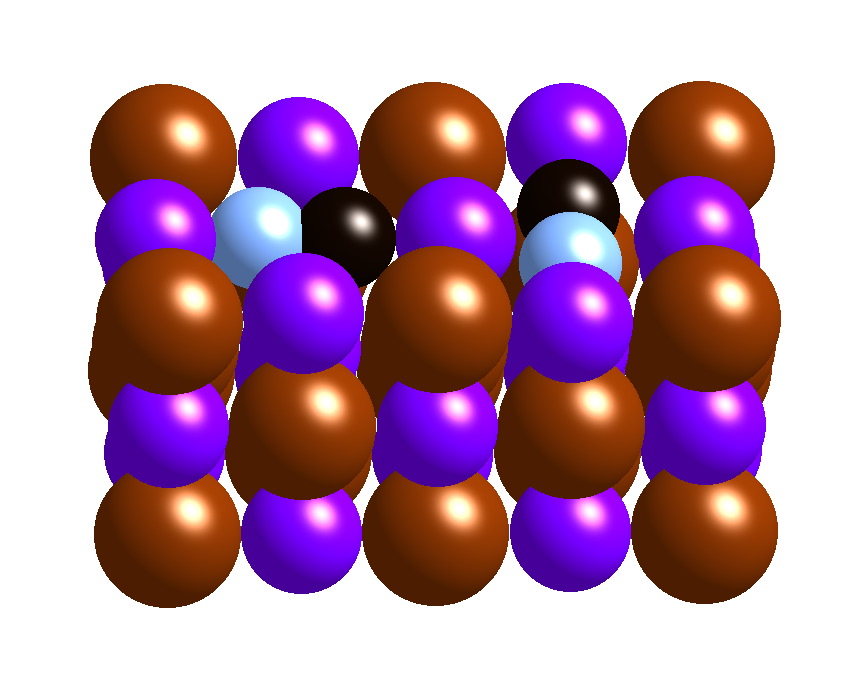
We have recently suggested a novel model to explain the above questions, where tunneling states are classified to symmetric and asymmetric with respect to local inversion (examples are \(180^\circ\) flips and \(90^\circ\) rotations of the CN impurity in the picture at the bottom left). The “symmetric” TLSs couple weakly to the phonons, yet gap the asymmetric TLSs at low energies – the DOS of the latter is shown at the bottom right. We are now interested in using the theory to calculate further relevant physical quantities, and in the rigorous generalization of the theory to amorphous solids. For more details see arXiv:0910.1283.

Dynamics of condensed particles in a few site system

Doron Cohen

The physics of \(N\) bosons in an \(M\) site system is described by the Bose-Hubbard Hamiltonian. The \(M=2\) problem is integrable and equivalent to \(j=N/2\) spin problem, while the \(M=3\) problem has both non-trivial topology and mixed phase space. Our studies concerns the analysis of fluctuations, occupation statistics and quantum stirring in such systems. The \(M=4\) problem is the minimal configuration for the study of quantum thermalization and many-body localization. Specifically we consider the equilibration of the occupation in a weakly coupled subsystems.

Bosonic Josephson junction: The time dependent dynamics of a Bosonic Josephson junction with no driving can be regarded as a quantum version of a pendulum. Adding driving to this system, we have studied the adiabatic-diabatic-sudden crossover of the many-body Landau-Zener dynamics; the Kapitza pendulum dynamics; and the Quantum Zeno dynamics due to erratic driving. In particular we have studied the stabilization and the suppression of collision-induced dephasing by periodic, erratic, or noisy driving.

Atomtronic Superfluid Circuits: Circuits with condensed bosons can support superflow. Such circuits, if realized, will be used as QUBITs (for quantum computation) or as SQUIDs (for sensing of acceleration or gravitation). We are studying the feasibility and the design considerations for such devices. The key is to develop a theory for the superfluidity in an atomtronic circuit. Such theory goes beyond the traditional framework of Landau and followers, since is involves Quantum chaos considerations.

Figure: Regime diagram for the stability of flow-states in a superfluid circuit. The axes are: the rotation frequency \(\Phi\) of the device; and the interaction u. On the right the stable regions are indicated by blue color. Red indicates instability.

 

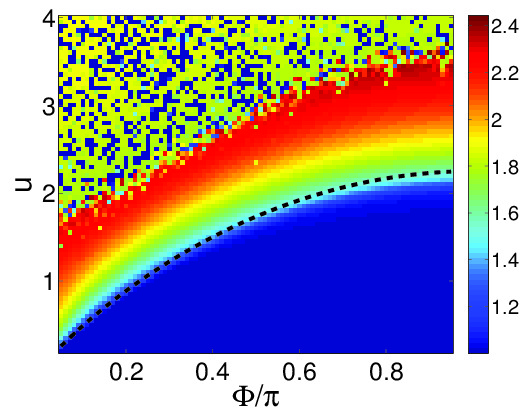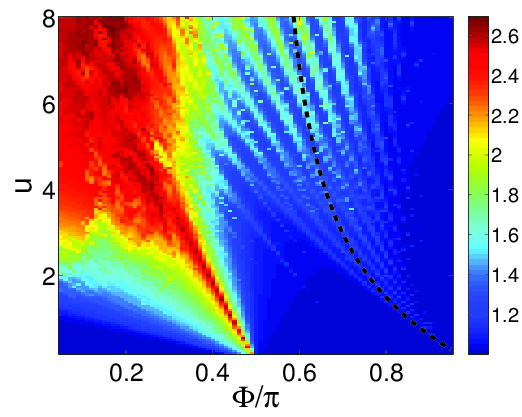Our recent studies are focused in Bose-Hubbard superfluid circuits. The expected results are novel due to the quantum chaos perspective. In particular we predict drastic differences between 3 site rings and rings that have more than 3 sites. In the former instability of flow states is due to swap of separatrices, while in the latter it has to do with a web of non-linear resonances. We also argue that it is not likely to observe coherent operation for rings that have a weak link and more than 5 sites.

For references click here
For more highlights click here