Non-equilibrium steady state of stochastic circuits

Doron Cohen

The study of systems with non-equilibrium steady state (NESS) has become of great interest in recent years. The paradigm for NESS is a system which is coupled to two equilibrated reservoirs "A" and "B" that are characterized by different temperatures \(T_A\) and \(T_B\). The steady state of the system is not canonical. A particular case of special interest is having one reservoirs (call it "A") that is replaced by a stationary driving source, while the relaxation is provided by a bath (call it "B") that has some finite temperature \(T_B\). This is still the same paradigm because formally the driving source "A" can be regarded as a bath that has an infinite temperature \(T_A=\infty\).

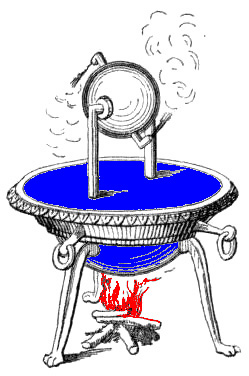Upper figure: Illustration of a prototype model system: a ring that is made up of N isolated sites with on site energies E_n. The ring is coupled to a heat reservoir (represented by the blue "environment") and subjected to a noisy driving field (represented by the red circle) that induces a current in the ring.

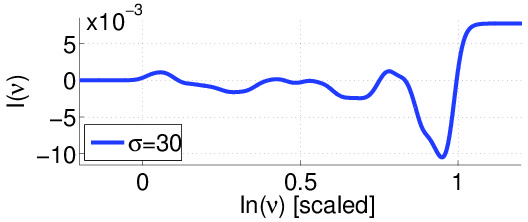
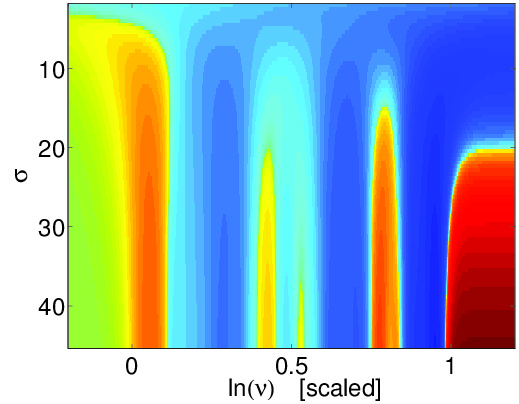
Lower figure: In the upper panel the current in the ring is plotted as a function of the scaled driving intensity. In the lower panel this dependence is imaged for various strengths ("sigma") of disorder (each row corresponds to one plot as above). More generally we have analyzed the statistics of the current over many realizations of the disorder.

In subsequent studies we have addressed questions that concern the relaxation of such currents, and how the relaxation depends on percolation and localization properties of the model. Currently we are trying to extend the theory, considering general stochastic active networks.

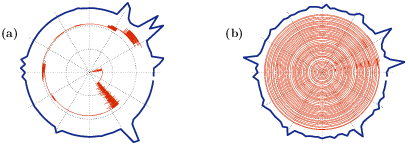
The above figure is taken form our Nature Scientific Report publication entitled "Percolation, sliding, localization and relaxation in topologically closed circuits". The radial direction is time and the angle is the position. (a) For small bias the dynamics is over-damped. (b) For large bias the dynamics is under-damped. The transition has to do with the de-localization of the eigen-modes, and surprisingly happens before the "sliding transition" that had been widely discussed in past literature.

For references click here
For more highlights click here

Dynamics of condensed particles in a few site system

Doron Cohen

The physics of \(N\) bosons in an \(M\) site system is described by the Bose-Hubbard Hamiltonian. The \(M=2\) problem is integrable and equivalent to \(j=N/2\) spin problem, while the \(M=3\) problem has both non-trivial topology and mixed phase space. Our studies concerns the analysis of fluctuations, occupation statistics and quantum stirring in such systems. The \(M=4\) problem is the minimal configuration for the study of quantum thermalization and many-body localization. Specifically we consider the equilibration of the occupation in a weakly coupled subsystems.

Bosonic Josephson junction: The time dependent dynamics of a Bosonic Josephson junction with no driving can be regarded as a quantum version of a pendulum. Adding driving to this system, we have studied the adiabatic-diabatic-sudden crossover of the many-body Landau-Zener dynamics; the Kapitza pendulum dynamics; and the Quantum Zeno dynamics due to erratic driving. In particular we have studied the stabilization and the suppression of collision-induced dephasing by periodic, erratic, or noisy driving.

Atomtronic Superfluid Circuits: Circuits with condensed bosons can support superflow. Such circuits, if realized, will be used as QUBITs (for quantum computation) or as SQUIDs (for sensing of acceleration or gravitation). We are studying the feasibility and the design considerations for such devices. The key is to develop a theory for the superfluidity in an atomtronic circuit. Such theory goes beyond the traditional framework of Landau and followers, since is involves Quantum chaos considerations.

Figure: Regime diagram for the stability of flow-states in a superfluid circuit. The axes are: the rotation frequency \(\Phi\) of the device; and the interaction u. On the right the stable regions are indicated by blue color. Red indicates instability.

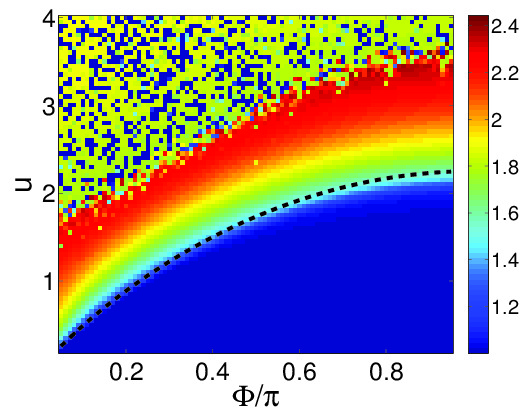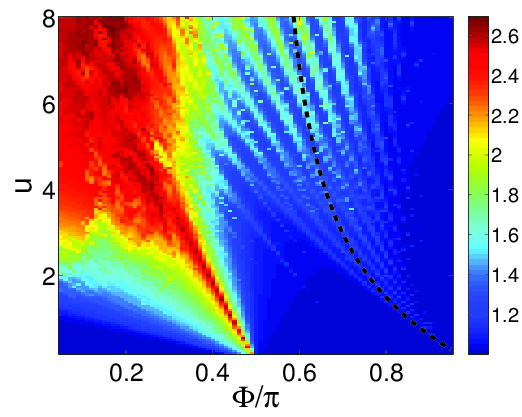Our recent studies are focused in Bose-Hubbard superfluid circuits. The expected results are novel due to the quantum chaos perspective. In particular we predict drastic differences between 3 site rings and rings that have more than 3 sites. In the former instability of flow states is due to swap of separatrices, while in the latter it has to do with a web of non-linear resonances. We also argue that it is not likely to observe coherent operation for rings that have a weak link and more than 5 sites.

For references click here
For more highlights click here