Non-equilibrium steady state of stochastic circuits
Doron Cohen
The study of systems with non-equilibrium steady state (NESS) has become of great interest in recent years. The paradigm for NESS is a system which is coupled to two equilibrated reservoirs "A" and "B" that are characterized by different temperatures \(T_A\) and \(T_B\). The steady state of the system is not canonical. A particular case of special interest is having one reservoirs (call it "A") that is replaced by a stationary driving source, while the relaxation is provided by a bath (call it "B") that has some finite temperature \(T_B\). This is still the same paradigm because formally the driving source "A" can be regarded as a bath that has an infinite temperature \(T_A=\infty\).
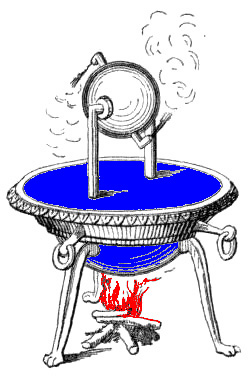  |
Upper figure: Illustration of a prototype model system: a ring that is made up of N isolated sites with on site energies E_n. The ring is coupled to a heat reservoir (represented by the blue "environment") and subjected to a noisy driving field (represented by the red circle) that induces a current in the ring.
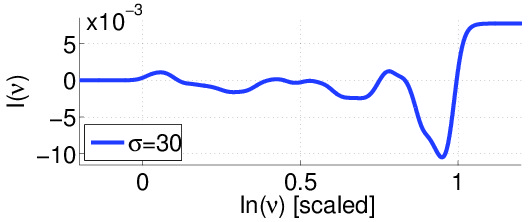
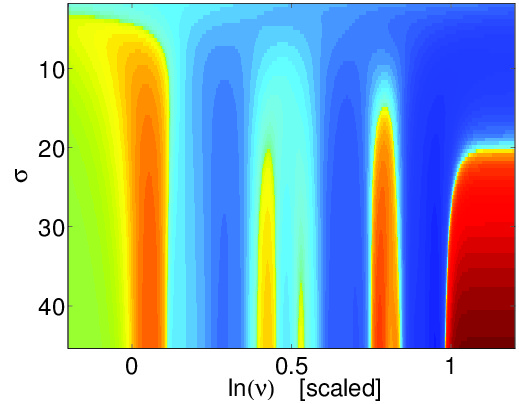
Lower figure: In the upper panel the current in the ring is plotted as a function of the scaled driving intensity. In the lower panel this dependence is imaged for various strengths ("sigma") of disorder (each row corresponds to one plot as above). More generally we have analyzed the statistics of the current over many realizations of the disorder.
In subsequent studies we have addressed questions that concern the relaxation of such currents, and how the relaxation depends on percolation and localization properties of the model. Currently we are trying to extend the theory, considering general stochastic active networks.
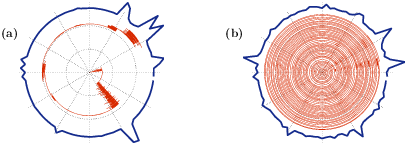
The above figure is taken form our Nature Scientific Report publication entitled "Percolation, sliding, localization and relaxation in topologically closed circuits". The radial direction is time and the angle is the position. (a) For small bias the dynamics is over-damped. (b) For large bias the dynamics is under-damped. The transition has to do with the de-localization of the eigen-modes, and surprisingly happens before the "sliding transition" that had been widely discussed in past literature.