The Atom Chip Group
Ron Folman
Quantum theory is one of the scientific revolutions of the 20th century. It is with us for nearly a century and we still don’t fully understand it and its implications. The quantum nature of atoms becomes dominant when their deBroglie wavelength becomes comparable to the size of the potential in which the atoms are held. This occurs at ultra low temperatures (<1μK). The wave properties of cold atoms (which are thus named "matter waves") can be exploited for fundamental measurements such as the study of nature's symmetries, search for new forces or analyzing the border between the quantum and classical worlds (with implications even to the question of freedom of thought). The field of quantum optics has made leaps in the past 15 years or so, and in this period 4 Nobel prizes have been awarded (1997, 2001, 2005, 2012).
Our main research tool is the AtomChip (Fig. 1). This device enables the manipulation and detection of isolated cold atoms for quantum operations. Such systems also have technological applications. For example, they have already set the best time standards; they are now being developed via interferometric schemes into acceleration sensors for ultra-accurate navigation systems, as well as for detecting minute changes in the gravitational field; magnetometry can be made so sensitive that it can be used for medical imaging of the brain; more futuristic applications involve secure communication (quantum cryptography) and the super-fast quantum computer.
The "AtomChip" group, and the nano-fabrication facility at Ben-Gurion University, combine in developing AtomChips for new fundamental insights into the laws of nature as well as new technological applications. Our students study for degrees in Theoretical and Experimental Physics (and combinations thereof), and are exposed to a variety of fundamental theory as well as advanced technology, ranging from lasers and optics, to electronics and computer interfaces. Our students have won numerous excellence awards in Israel and abroad, and have found excellent jobs in the industry and academia. For example, one of our recent PhD graduates was invited by a Nobel Laureate to MIT for a post-doc position.
See our “what's new” page for more information.
In recent years we have published articles in the most prestigious journals such as Science, Science advances, Nature communications, and Physical Review Letters. As an example, see our unique project to put a clock in two places at the same time which was published in 2015 in the prestigious Science magazine. Watch a short video that describes our experiment: English / Hebrew
Bottom line: We talk to atoms, and you are invited to talk to them too!

Figure 1: An Atom Chip recently fabricated at BGU, with current carrying wires forming magnetic traps and guides for cold atoms. (published in Science 2008).

Figure 2: An interference pattern made by matter-waves in our lab. This interference pattern is the direct result of putting a clock in two places at the same time, as allowed by quantum rules. This experiment measured the interface between quantum theory and general relativity (published in Science 2015). See also: English / Hebrew
Constraints on quantum mechanics
Daniel Rohrlich
The axioms of quantum mechanics are well known, but most of them are abstract and mathematical. They are not clear physical statements like the two axioms of special relativity, defining a maximal signalling speed (the speed of light) and a fundamental symmetry (Lorentz invariance). Can we derive quantum mechanics from clear physical statements? Or, if we are not there yet, can we at least formulate clear physical statements that constrain quantum mechanics and any generalization of quantum mechanics?
Suprisingly - to say the least - the assumption that every physical value exists before we measure it (regardless of what goes on elsewhere) does not constrain quantum mechanics. This "local realism" assumption implies Bell's inequality, and quantum mechanics violates Bell's inequality. In particular, one form of Bell's inequality says that a certain combination \(C\) of measured correlations must not exceed \(2\) . But in quantum mechanics, \(C\) can reach \(2\sqrt{2}\) . This fact is called "Tsirelson's bound", and it is a theorem of quantum mechanics.
Quantum mechanics does obey the no-signalling constraint (the first axiom of special relativity): quantum correlations are useless for sending faster-than-light signals. Does Tsirelson's bound follow from this constraint? No, it does not; as Sandu Popescu and I showed in Ref. [1], hypothetical "superquantum" correlations (now also called Popescu-Rohrlich-box ("PR-box") correlations as in Ref. [2]) can reach \(C=4\) without violating the no-signalling constraint. So where does Tsirelson's bound come from?
Quantum mechanics obeys another constraint, besides no-signalling: it has a classical limit, in which Planck's constant hh vanishes and all physical values are measurable. In this limit, I have found [3] that PR-box correlations do not obey the no-signalling constraint. Generalized to all stronger-than-quantum correlations, this result is a derivation of Tsirelson's bound without assuming quantum mechanics. So we can derive at least a part of quantum mechanics from the two axioms of no-signalling and a classical limit, together with the negation of local realism.
For further details, see Refs. [3−5][3−5] . The work of [4][4] continues in collaboration with Avishy Carmi and Daniel Moskovich of the Mechanical Engineering Department and the Center for Quantum Information Science and Technology at BGU.
- S. Popescu and D. Rohrlich, Quantum nonlocality as an axiom, Found. Phys. 24 (1994) 379.
- J. Barrett and S. Pironio, Popescu-Rohrlich Correlations as a Unit of Nonlocality, Phys. Rev. Lett. 95, 140401 (2005).
- D. Rohrlich, PR-box correlations have no classical limit, in Quantum Theory: A Two-Time Success Story (Yakir Aharonov Festschrift), eds. D. C. Struppa and J. M. Tollaksen (New York: Springer), 2013, pp. 205-211.
- D. Rohrlich, Stronger-than-quantum bipartite correlations violate relativistic causality in the classical limit.
- Video of my talk at the Aharonov-80 Conference in 2012 at Chapman University.
Pressure Induced Structural and Electrical Phase Transitions in disordered materials: Silicon monoxide and the Anderson transition
Reuben Shuker
Application of very high pressure significantly alters the nature of intermolecular interaction, chemical bonding, molecular configuration, and crystal structure of solids. Practically we use Diamond Anvil Cell (Fig. 1) to produce pressures in the range from 1 and 40 GPa. Electronic correlations effects induced by high pressure results unusual phase transitions. Our main interest is focused on amorphous systems such as silicon
monoxide, where we observed an insulator to metal transition at pressure of 12 GPa (all in the amorphous phase). The temperature dependence of the conductivity is in very good agreement with the Anderson model for amorphous materials indicating Anderson transition in disordered systems. The material response to high pressure is studied by a variety of experimental methods: x-ray diffraction using synchrotron radiation, IR spectroscopy, Raman scattering and electrical conductivity measurements.
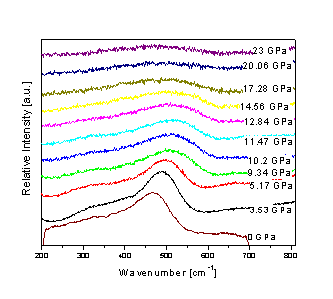
For example, the Raman scattering spectra and the pressure dependence of the resistivity for SiO sample are presented in figures 2 and 3 respectively. IR and Raman results assign bond-bending to Raman active modes since it is hardened under pressure, whereas IR active modes are dominated by bond-stretching modes.
The miniature sample (~100 μm in diameter) we use in high pressure studies makes the electrical resistivity measurements a challenging experimental problem. However, we managed to observe a dramatic drop of the resistivity on one hand (Fig. 3), and significant change in the temperature dependence of the resistance on the other, both happen at pressure 12 GPa. Short-rang order on the molecular scale helps us explain the insulator to metal transition in terms of Anderson's theory of localization, where lone-pair electrons create states in the gap.
 |
 |
 |
| Figure 1: Diamond Anvil Cell | Figure 2: The Raman scattering spectra of SiO sample at different pressures. | Figure 3: The pressure dependence of the resistivity for SiO sample. |
Quantum Interferences and Lasing without inversion
Reuben Shuker
Quantum-interference-related phenomena have great interest in many aspects of physics. Quantum interference between two independent quantum channels in three-level systems gives rise to various coherent phenomena, such as electromagnetically induced transparency (EIT), coherent population trapping (CPT), lasing/gain without inversion (LWI/GWI), enhancement of refraction index, sub- and super-luminal light propagation etc. These quantum-interference-related phenomena open a wide-range perspective for new type of phase-sensitive spectroscopy. In particular, the movie in Fig.1 shows the absorption/dispersion properties of the atom controlled by various parameters. Another example is the possibility to get sub-natural line widths (see movie in Fig.2).
 |
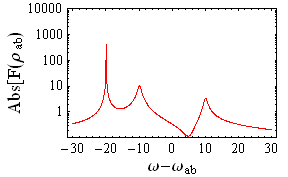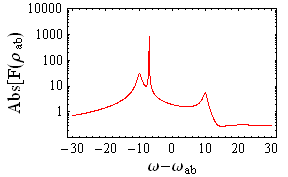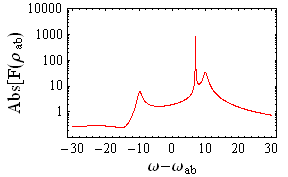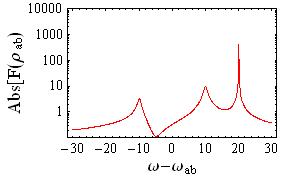 |
| Figure 1: Phase-controlled absorption (red) and dispersion (blue). | Figure 2: Sub-natural-width peak. |
Development of Novel Lasers
Salman (Zamik) Rosenwaks
In our group, we focus on experimental and theoretical studies of diode pumped alkali lasers (DPALs)

Figure 1: Low Lying States of Alkali Atoms and Excitation and Lasing Processes in DPALs
Further reading: Visit my website
Attosecond Science and Nanophotonics group
Eugene Frumker
In our group, we focus on both experimental and theoretical studies at the interface of ultrafast nonlinear optics, attosecond science and nanoscience.
More specifically, our work involves generation, measurement and control of the interaction of light and matter in atoms,
molecules and nanosystems in space and time at extremely short (attosecond=\(10^{-18}\)sec) time scales.
Our interests range from fundamental physical phenomena associated with these processes to practical applications.
There are currently positions available for excellent and highly motivated students at MSc/PhD levels.
We also have exciting projects for the undergraduate students.
For further details, please contact Eugene Frumker

Figure 1: Attosecond burst interference lies at the heart of
high harmonic generation from oriented molecules.
Further reading: Visit our website