Dynamics of condensed particles in a few site system

Doron Cohen

The physics of \(N\) bosons in an \(M\) site system is described by the Bose-Hubbard Hamiltonian. The \(M=2\) problem is integrable and equivalent to \(j=N/2\) spin problem, while the \(M=3\) problem has both non-trivial topology and mixed phase space. Our studies concerns the analysis of fluctuations, occupation statistics and quantum stirring in such systems. The \(M=4\) problem is the minimal configuration for the study of quantum thermalization and many-body localization. Specifically we consider the equilibration of the occupation in a weakly coupled subsystems.

Bosonic Josephson junction: The time dependent dynamics of a Bosonic Josephson junction with no driving can be regarded as a quantum version of a pendulum. Adding driving to this system, we have studied the adiabatic-diabatic-sudden crossover of the many-body Landau-Zener dynamics; the Kapitza pendulum dynamics; and the Quantum Zeno dynamics due to erratic driving. In particular we have studied the stabilization and the suppression of collision-induced dephasing by periodic, erratic, or noisy driving.

Atomtronic Superfluid Circuits: Circuits with condensed bosons can support superflow. Such circuits, if realized, will be used as QUBITs (for quantum computation) or as SQUIDs (for sensing of acceleration or gravitation). We are studying the feasibility and the design considerations for such devices. The key is to develop a theory for the superfluidity in an atomtronic circuit. Such theory goes beyond the traditional framework of Landau and followers, since is involves Quantum chaos considerations.

Figure: Regime diagram for the stability of flow-states in a superfluid circuit. The axes are: the rotation frequency \(\Phi\) of the device; and the interaction u. On the right the stable regions are indicated by blue color. Red indicates instability.

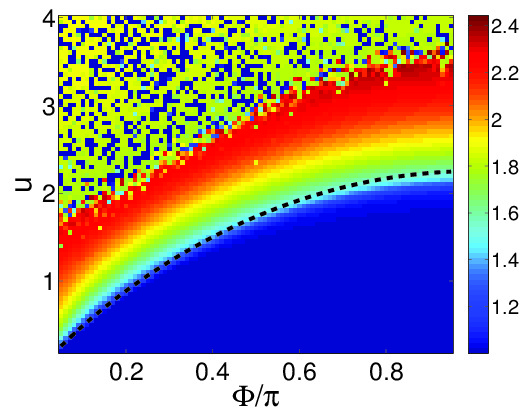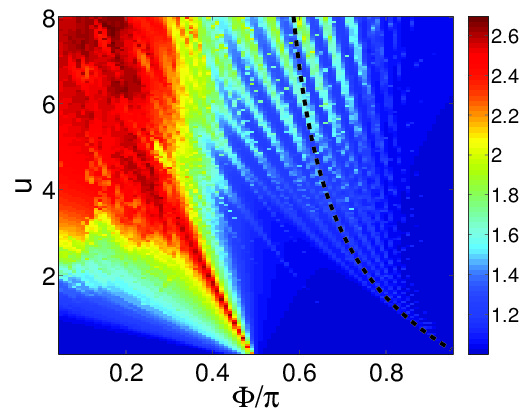Our recent studies are focused in Bose-Hubbard superfluid circuits. The expected results are novel due to the quantum chaos perspective. In particular we predict drastic differences between 3 site rings and rings that have more than 3 sites. In the former instability of flow states is due to swap of separatrices, while in the latter it has to do with a web of non-linear resonances. We also argue that it is not likely to observe coherent operation for rings that have a weak link and more than 5 sites.

For references click here
For more highlights click here