BGU Physics Department logo

Bar Lev, Yevgeny

Faculty
Bar Lev, Yevgeny
Email
ybarlev@bgu.ac.il
Office
54/329
Phone
08-6472125
Website
https://sites.physics.bgu.ac.il/ybarlev/
Research type
Theoretical
Research topics

Condensed matter theory, thermalization, nonequillibrium

Researcher identification
ORCID, Google Scholar

Responsibilities

Research group

  1. MSc student, Guy Almog Graf
  2. PhD student, Emuna Rimon

Past postdocs *

  1. Devendra Singh Bhakuni (2023)
  2. Alexander James Duthie (2023)
  3. Wouter Buijsman (2023)
  4. Talia Love Mergold (2021)

Past graduate students *

  1. Adam Gitter, MSc (2024)
  2. Guy Zisling, MSc (2022)

Past undergraduate students *

  1. Ben Shpigel (2024)
  2. Adam Gitter (2021)
  3. Rotem Berman (2021)
  4. Osher Shoval (2020)
  5. Omer Feinberg (2019)
  6. Avrham Aton (2019)
  7. Amir Bialer (2019)
* Past students / postdocs data might be incomplete

Research highlights

Nonequillibrium dynamics

Nonequillibrium dynamics
Spreading of density excitation in a two-dimensional Fermi-Hubbard model

While conventionally condendsed matter theory was moslty concerned with equilibrium or stationary states situations, recent theoretical and experimental progress spurred interest in nonequillibrium. In our group we study various situations of nonequillibrium dynamics, such as transport, quenches and external driving.

Disordered Systems

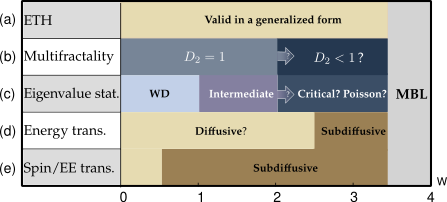
Disordered Systems
Characterization of the anomalous ergodic phase, leaves many questions open.

Disorder allows avoiding thermalization and defy conventional statistical mechanics, through the mechanisms of Anderson or many-body localization. We study these ergodicity breaking mechanisms in detail. In particular the nature of transport and correlations spreading in systems on the verge of localization.

Publications

  1. Atanasova, H. and Erpenbeck, A. and Gull, E. and Bar Lev, Y. and Cohen, G., "Stark Many-Body Localization In Interacting Infinite Dimensional Systems", Phys. Rev. Lett. 132, 166301 (2024)
  2. Bar Lev, Y. and Lazarides, A., "Discrete Time Crystals In Unbounded Potentials", Phys. Rev. Lett. 133, 200401 (2024)
  3. Bhakuni, D.S. and Bar Lev, Y., "Dynamic Scaling Relation In Quantum Many-Body Systems", Phys. Rev. B 110, 014203 (2024)
  4. Bhakuni, D.S. and Lezama, T. L. M. , and Bar Lev, Y., "Noise-Induced Transport In The Aubry-André-Harper Model", SciPost Phys. Core 7, 023 (2024)
  5. Kloss, B. and Halimeh, J.C. and Lazarides, A. and Bar Lev, Y., "Absence Of Localization In Interacting Spin Chains With A Discrete Symmetry", Nat Commun 14, 3778 (2023)
  6. L. M. Lezama, T. and Bar Lev, Y. and Santos, L.F., "Temporal Fluctuations Of Correlators In Integrable And Chaotic Quantum Systems", SciPost Phys. 15, 244 (2023)
  7. Lebel, Y. and Santos, L.F. and Bar Lev, Y., "Chaos Enhancement In Large-Spin Chains", SciPost Phys. 15, 022 (2023)
  8. Guy Zisling and Dante M. Kennes and Yevgeny Bar Lev, "Transport In Stark Many Body Localized Systems", Phys. Rev. B 105, L140201 (2022)
  9. Talía L. M. Lezama and Yevgeny Bar Lev, "Logarithmic, Noise-Induced Dynamics In The Anderson Insulator", SciPost Phys. 12, 174 (2022)
  10. Wouter Buijsman and Yevgeny Bar Lev, "Circular Rosenzweig-Porter Random Matrix Ensemble", SciPost Phys. 12, 082 (2022)
  11. Devendra Singh Bhakuni and Lea F. Santos and Yevgeny Bar Lev, "Suppression of heating by long-range interactions in periodically driven spin chains", Phys. Rev. B 104, L14030 (2021)
  12. Talía L. M. Lezama and E. Jonathan Torres-Herrera and Francisco Pérez-Bernal and Yevgeny Bar Lev and Lea F. Santos, "Thermalization Time In Many-Body Quantum Systems", Phys. Rev. B 104, 085117 (2021)
  13. Zisling, G. and Santos, L.F. and Bar Lev, Y., "How Many Particles Make Up A Chaotic Many-Body Quantum System?", SciPost Phys 10, 088 (2021)
  14. Kloss, B. Reichman. D.R. and Bar Lev, Y, "Studying Dynamics In Two-Dimensional Quantum Lattices Using Tree Tensor Network States", SciPost Phys. 9, 070 (2020)
  15. Kloss, B. and Bar Lev, Y., "Spin Transport In Disordered Long-Range Interacting Spin Chain", Phys. Rev. B 102, 060201(R) (2020)
  16. Luitz, D. J. and Bar Lev, Y., "Absence of slow particle transport in the many-body localized phase", Phys. Rev. B 102, 100202(R) (2020)
  17. Luitz, D.J. and Khaymovich, I. and Bar Lev, Y., "Multifractality And Its Role In Anomalous Transport In The Disordered XXZ Spin-Chain", SciPost Phys. Core 2, 006 (2020)
  18. Kloss, B. and Bar Lev, Y., "Spin Transport In A Long-Range-Interacting Spin Chain", Phys. Rev. A 99, 032114 (2019)
  19. Luitz, D.J. and Bar Lev, Y., "Emergent Locality In Systems With Power-Law Interactions", Phys. Rev. A 99, 010105(R) (2019)