Phase measurements in quantum mechanics
Amnon Aharony
When a wave splits through two slits, one obtains an interference pattern which depends on the phase difference between the two paths. Recently, experiments studied mesoscopic solid state interferometers. A magnetic flux \Phi enclosed between the paths adds a Aharonov-Bohm (AB) phase difference, yielding a current with a term containing \(\cos\left(2\pi e\Phi/hc+\beta\right)\) . The phase shift \(\beta\) was interpreted as the intrinsic phase \(\alpha\) of the quantum transmission via a quantum dot (QD) located on one of the paths. This intrinsic phase is important for studies of the quantum properties of the QD, relevant to many nanoscopic devices. We have shown that in fact, the measured \(\beta\) is usually not equal to αα ; except for very specific conditions (not yet discussed in the textbook chapters on the AB interferometer), the measured phase shift is due to losses of current out of the paths. We have then found theoretical conditions for when \(\beta=\alpha\). We have also given detailed predictions for the conductance of a closed interferometer (with no losses), and shown that the AB oscillations are strongly affected by the finite width of the interferometer's arms (see Fig. 2). Given the complications of the interpretations of such measurements, we have recently proposed an alternative: the quantum noise of the current through a quantum dot was shown to also contain information on the transmission phase.
 |
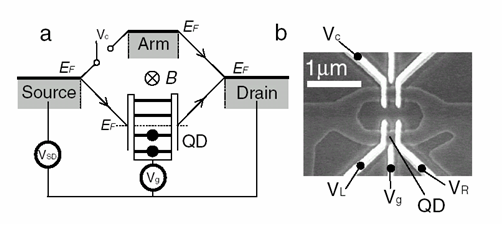 |
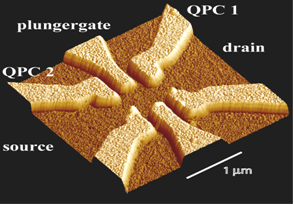
| Figure 1: electrodes on top of a two-dimensional electron gas, determining the potential seen by the electrons. The quantum dot, which can capture or scatter electrons, is in the center. | Figure 2: Right: electrodes in the AB interferometer. Left: schematic picture of the interferometer, with several bound states on the quantum dot, which sits on one arm, and with the magnetic field B in the center. |
- Relevant publications are listed in
Magnetism and ferroelectricity in rare earth oxides
Amnon Aharony
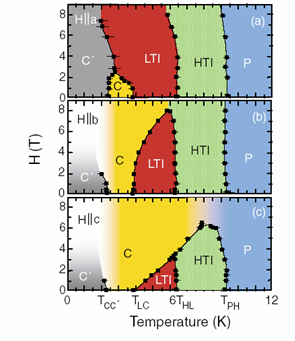
Insulating rare-earth oxides often exhibit rich magnetic phase diagrams, with interesting competing magnetic structures. Often, these phase diagrams are due to structures which are close to cubic or tetragonal. In these highly symmetric structures, the magnetic ground states are highly degenerate, implying magnetic frustration. We have studied several mechanisms which lift the frustration and yield a variety of magnetic ordered states. One mechanism involves quantum fluctuations. The zero point motion associated with these fluctuations creates "order out of disorder", and chooses some ground states over others. The second mechanism involves small magnetic anisotropies, usually due to spin-orbit interactions. Again, these anisotropies lift the degeneracy, and pick specific structures. Examples include several cuprates (the parents of high temperature superconductors) and nickel vanadate, whose structure is close to a planar Kagome lattice. The figure shows the temperature-magnetic field phase diagram of the latter material, which contains various types of (commensurate and incommensurate) magnetic order. Interestingly, this material shows multiferroic behavior: the low temperature incommensurate magnetic phase ("LTI") also exhibits ferroelectric order, which can thus be switched on and off by both a magnetic and an electric field. This has potential applications for spintronics.