Phase measurements in quantum mechanics
Amnon Aharony
When a wave splits through two slits, one obtains an interference pattern which depends on the phase difference between the two paths. Recently, experiments studied mesoscopic solid state interferometers. A magnetic flux \Phi enclosed between the paths adds a Aharonov-Bohm (AB) phase difference, yielding a current with a term containing \(\cos\left(2\pi e\Phi/hc+\beta\right)\) . The phase shift \(\beta\) was interpreted as the intrinsic phase \(\alpha\) of the quantum transmission via a quantum dot (QD) located on one of the paths. This intrinsic phase is important for studies of the quantum properties of the QD, relevant to many nanoscopic devices. We have shown that in fact, the measured \(\beta\) is usually not equal to αα ; except for very specific conditions (not yet discussed in the textbook chapters on the AB interferometer), the measured phase shift is due to losses of current out of the paths. We have then found theoretical conditions for when \(\beta=\alpha\). We have also given detailed predictions for the conductance of a closed interferometer (with no losses), and shown that the AB oscillations are strongly affected by the finite width of the interferometer's arms (see Fig. 2). Given the complications of the interpretations of such measurements, we have recently proposed an alternative: the quantum noise of the current through a quantum dot was shown to also contain information on the transmission phase.
 |
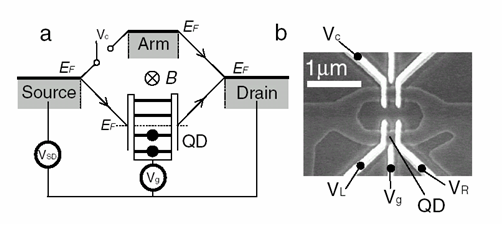 |
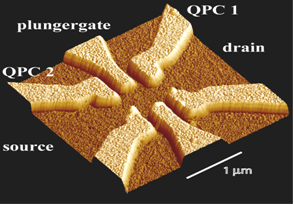
| Figure 1: electrodes on top of a two-dimensional electron gas, determining the potential seen by the electrons. The quantum dot, which can capture or scatter electrons, is in the center. | Figure 2: Right: electrodes in the AB interferometer. Left: schematic picture of the interferometer, with several bound states on the quantum dot, which sits on one arm, and with the magnetic field B in the center. |
- Relevant publications are listed in