Uri Keshet

Sample projets (outdated): (back to research highlights)
	Self similar ultra-relativistic jet solution
	Analytic solutions for hydrodynamic and magnetohydrodynamic flows
	Core collapse supernovae
	Radio halos and relics
	Spiral flows in galaxy clusters
	Cold fronts in galaxy clusters
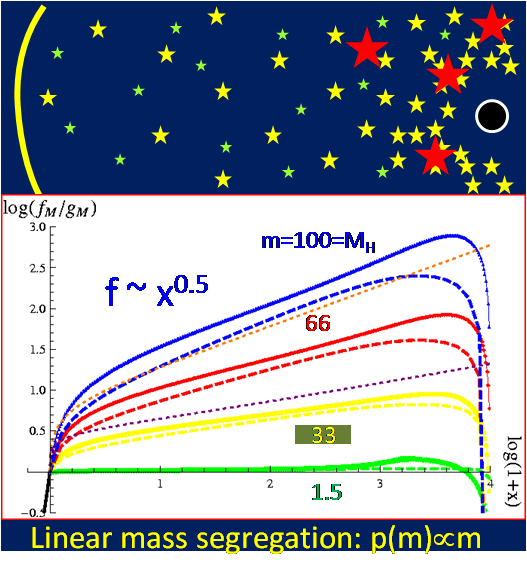
	Bahcall & Wolf (1976,1977) have shown that within the radius of influence of a massive black hole, stars of different masses segregate, each species forming a power-law density cusp. The upper left image illustrates mass segregation of stars (light stars in green, intermediate mass-yellow, and massive-red) around a massive black hole (black disk). We derived an analytic solution for the energy distribution f(x,m) of stars with an arbitrary mass function g(m) (illustrated in bottom left image). 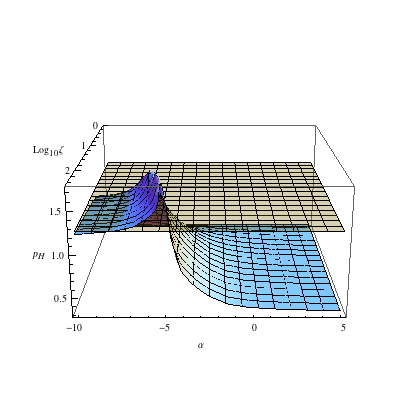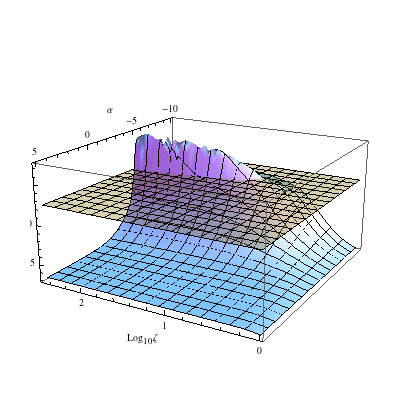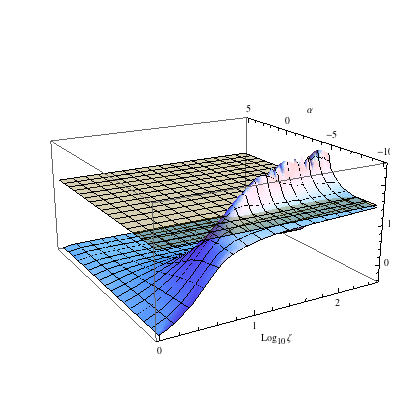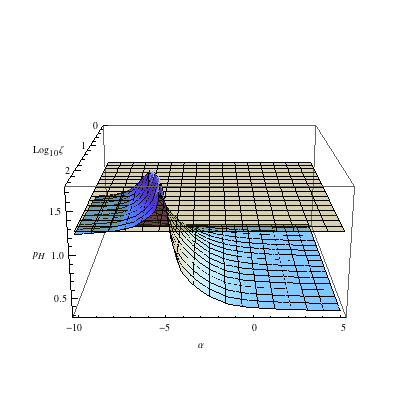At intermediate distances f~x^p, where p(m)=m/4M and M is an averaged stellar mass (see details). The right panel shows the landscape of the energy power-law indices pH of the most massive stars, for different power-law mass functions g(mL<m<mH)~m^α, as a function of power-law index α and the mass range ζ=mH/mL.
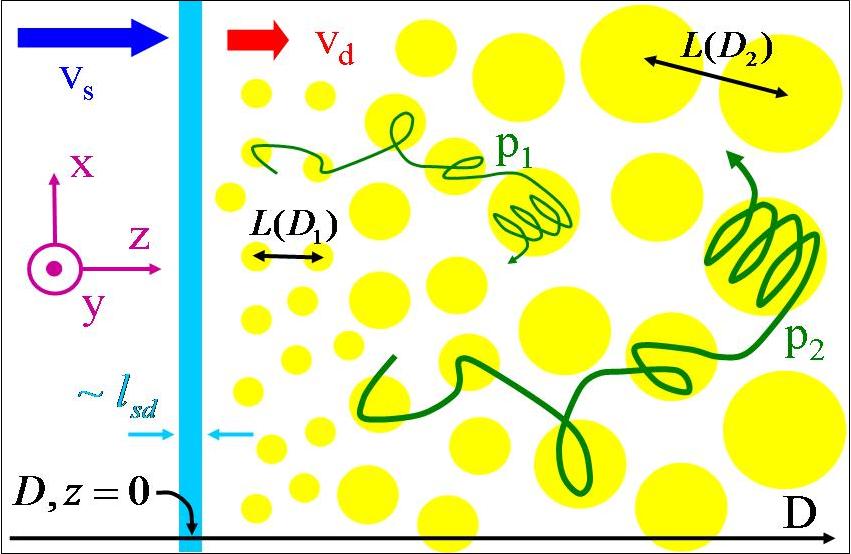
	Modelling a collisionless shock requires a self-consistent treatment of the electromagnetic field and the plasma, including the high energy tail which plays an important role in strong shocks. Motivated by γ-ray burst observations, we derived the scalings of self-similar solutions where the plasma is approximated as a combination of kinetic and MHD components (left: cartoon of downstream structure). 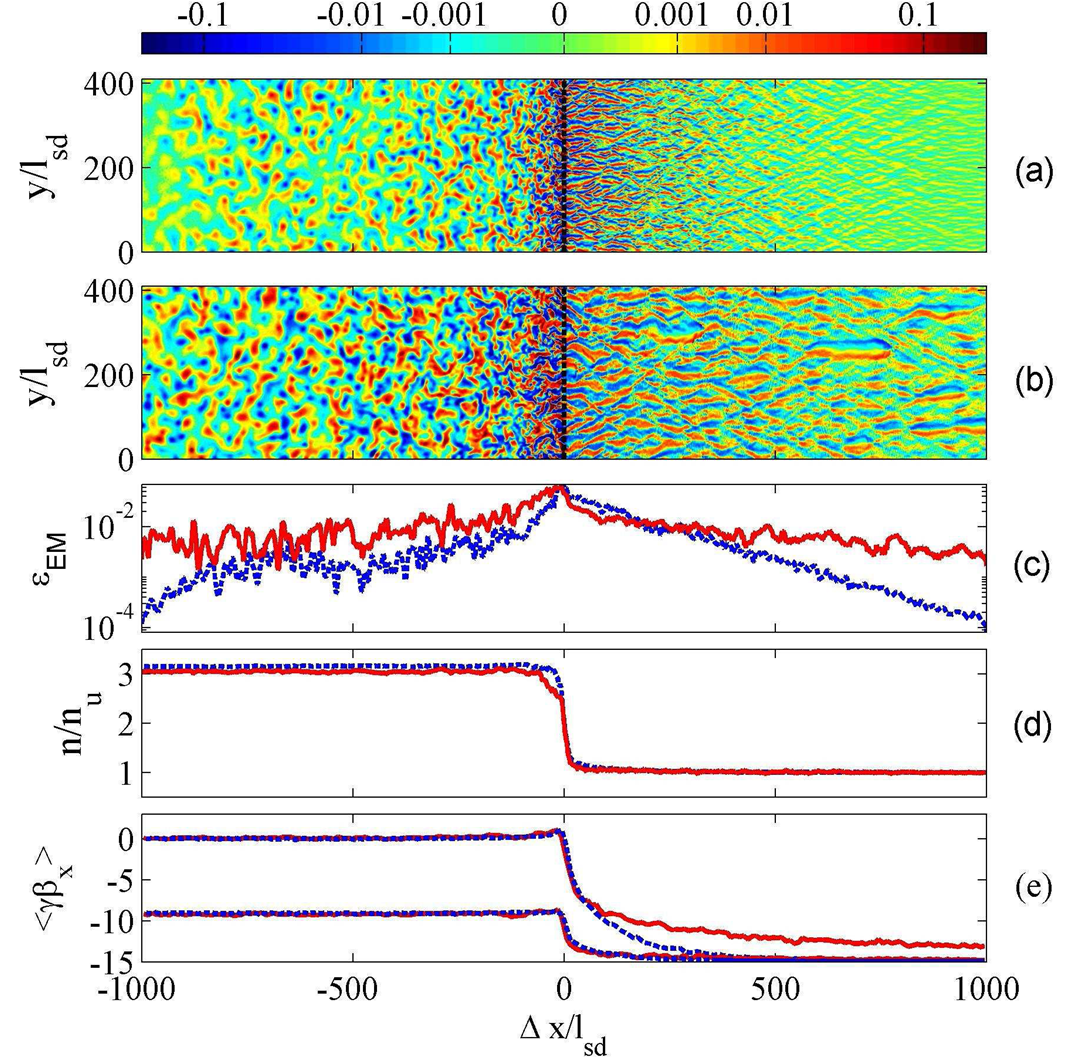Numerical simulations, notably particle in cell (PIC), are gradually probing more advanced stages in the evolution of shocks. We used ab-initio PIC simulations to demonstrate that the particle distributCCCion and the magnetic field evolve together over long time scales, not probed previously. The image on the right shows the spatial structure (in the shock frame; upstream is to the right) of a shock at early (panel a; blue curves) and late (panel b; red curves) times.
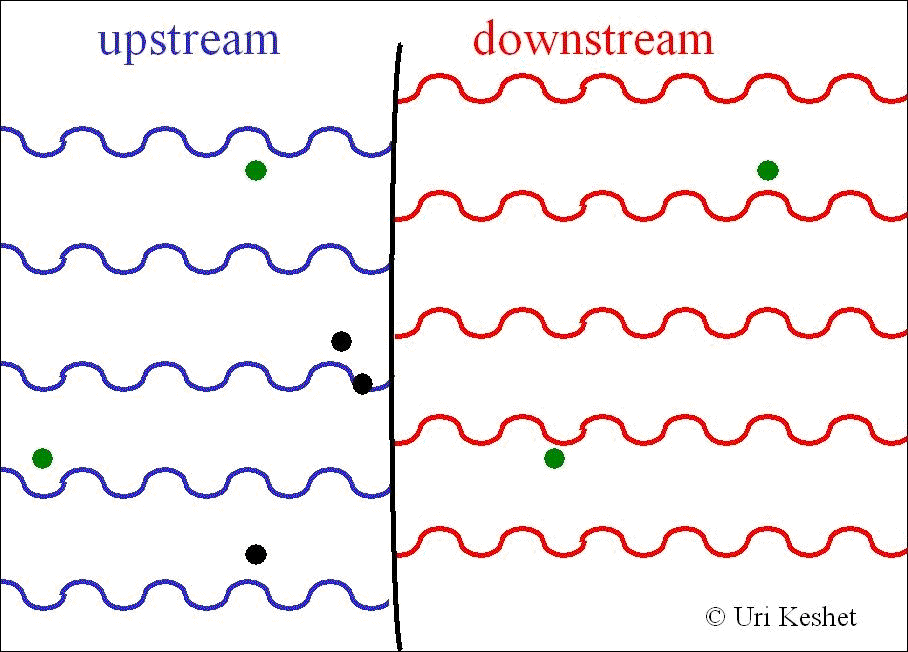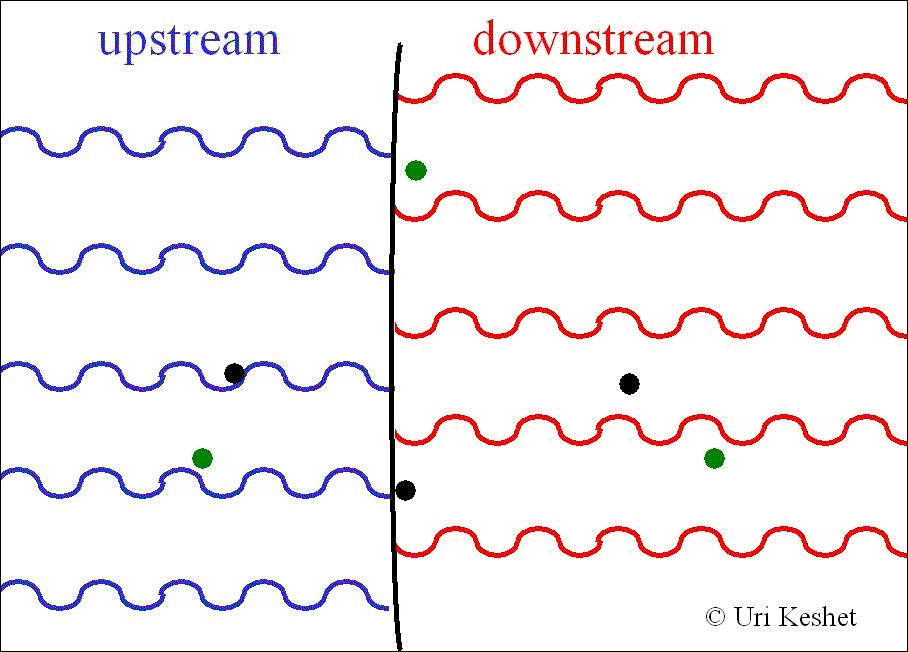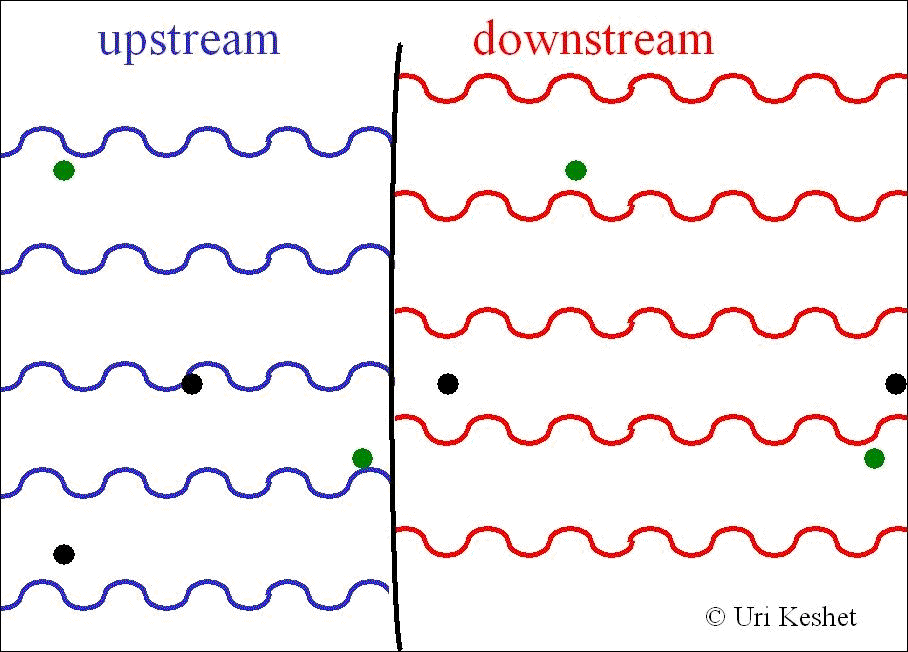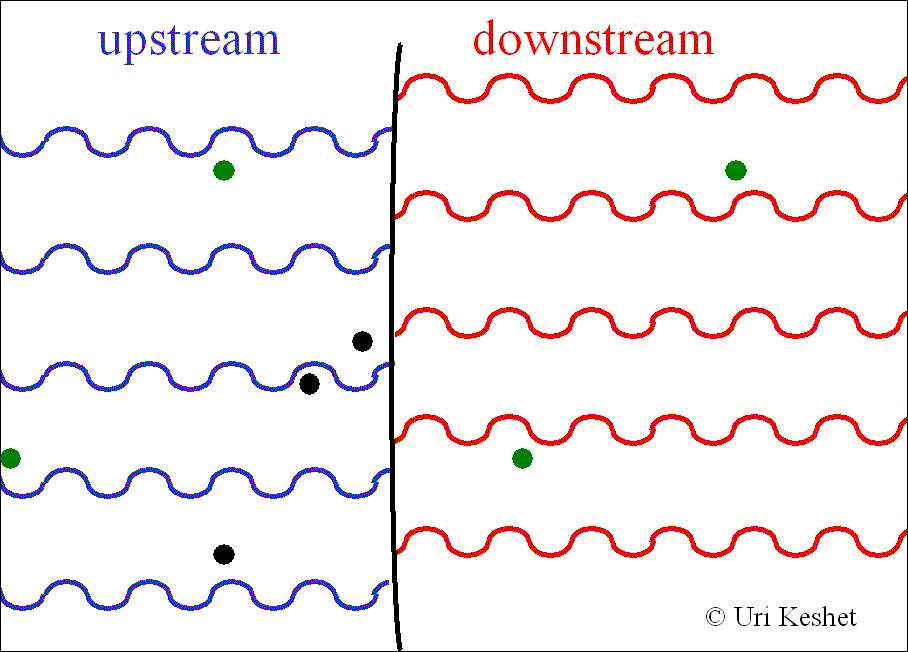	Collisionless shocks are thought to Fermi accelerate a power-law spectrum of charged particles by repeatedly scattering them across the shock front (left: illustrating one Fermi cycle). For isotropic diffusion the momentum spectral index was found to be s=(3β_u-2β_uβ_d²+β_u³)/(β_u-β_d), where β is the shock frame fluid velocity normalized to the speed of light (right panel: s for different equations of state). For ultrarelativistic shocks this gives s=38/9, in agreement with GRB afterglows. However, for relativistic shocks s is sensitive to the diffusion function, especially downstream.
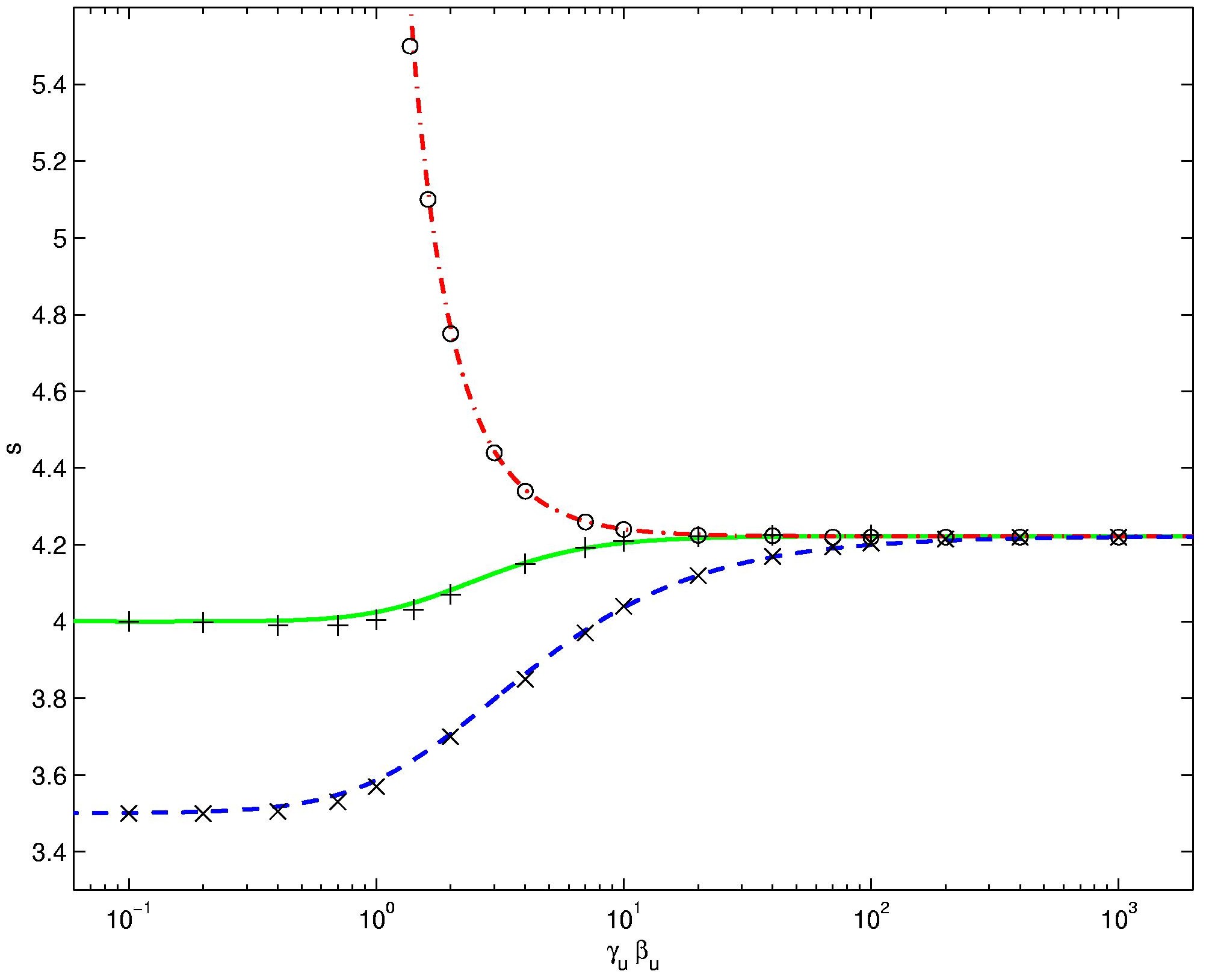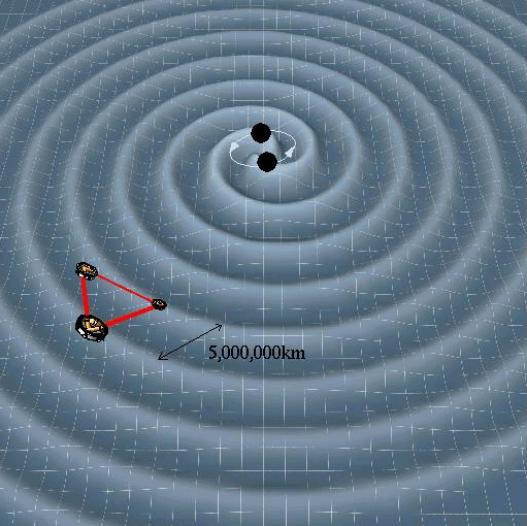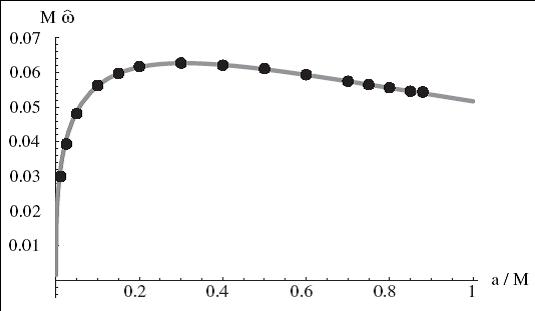
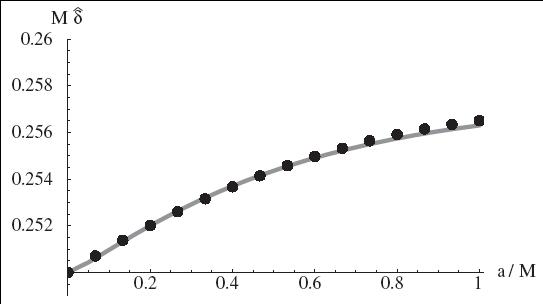
	Black holes have characteristic spectra of ringing (quasinormal) modes characterizing their perturbations, manifest for example as gravitational waves emitted in the last stages of black hole merger (left image: LISA artist impression). These and related resonances depend only on black hole parameters (mass, rotation and charge) and general relativity - no equation of state is involved. They share some similarities with atomic spectra (e.g. possible selection rules). The intermediate and asymptotic (right image) quasinormal spectrum and greybody factors of a general (Kerr-Newman) black hole were analytically derived [1, 2 ,3], providing clues on quantum gravity.
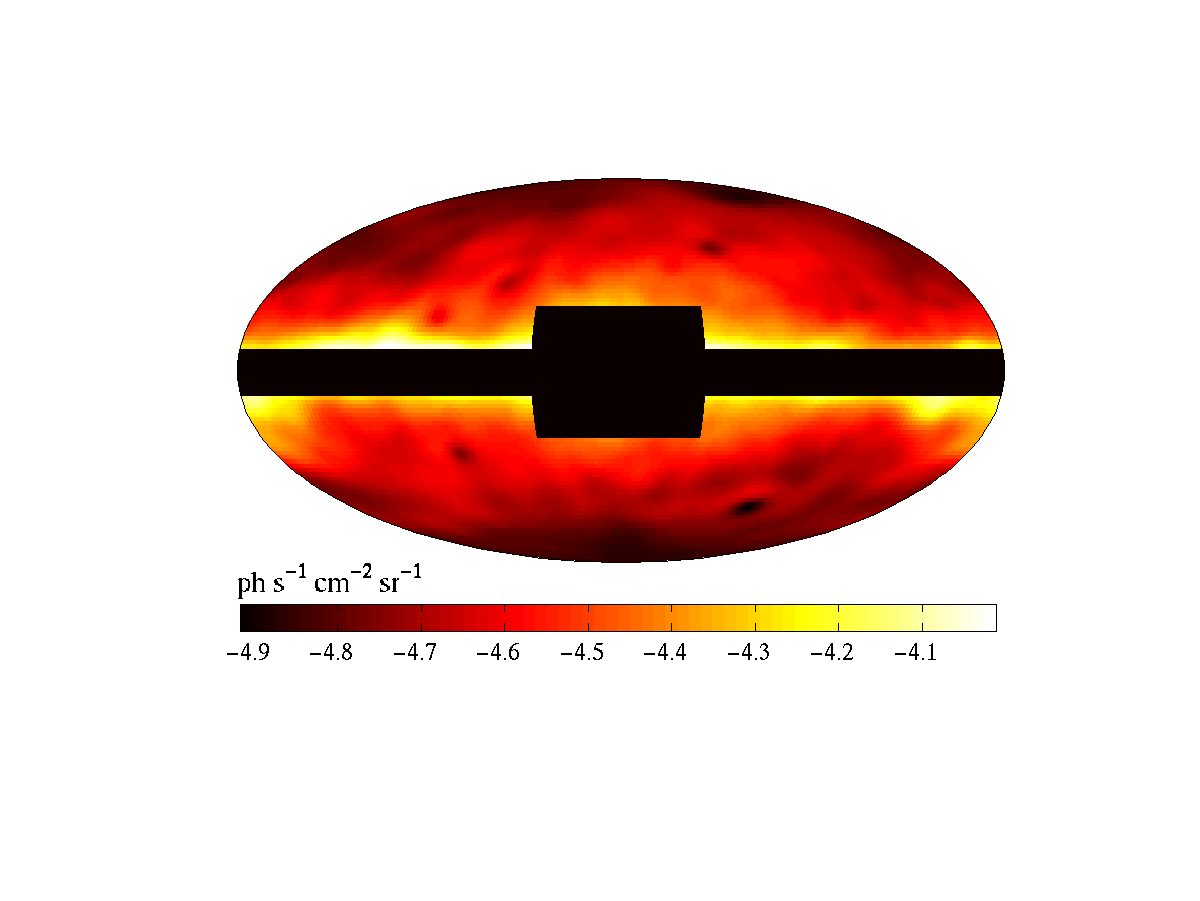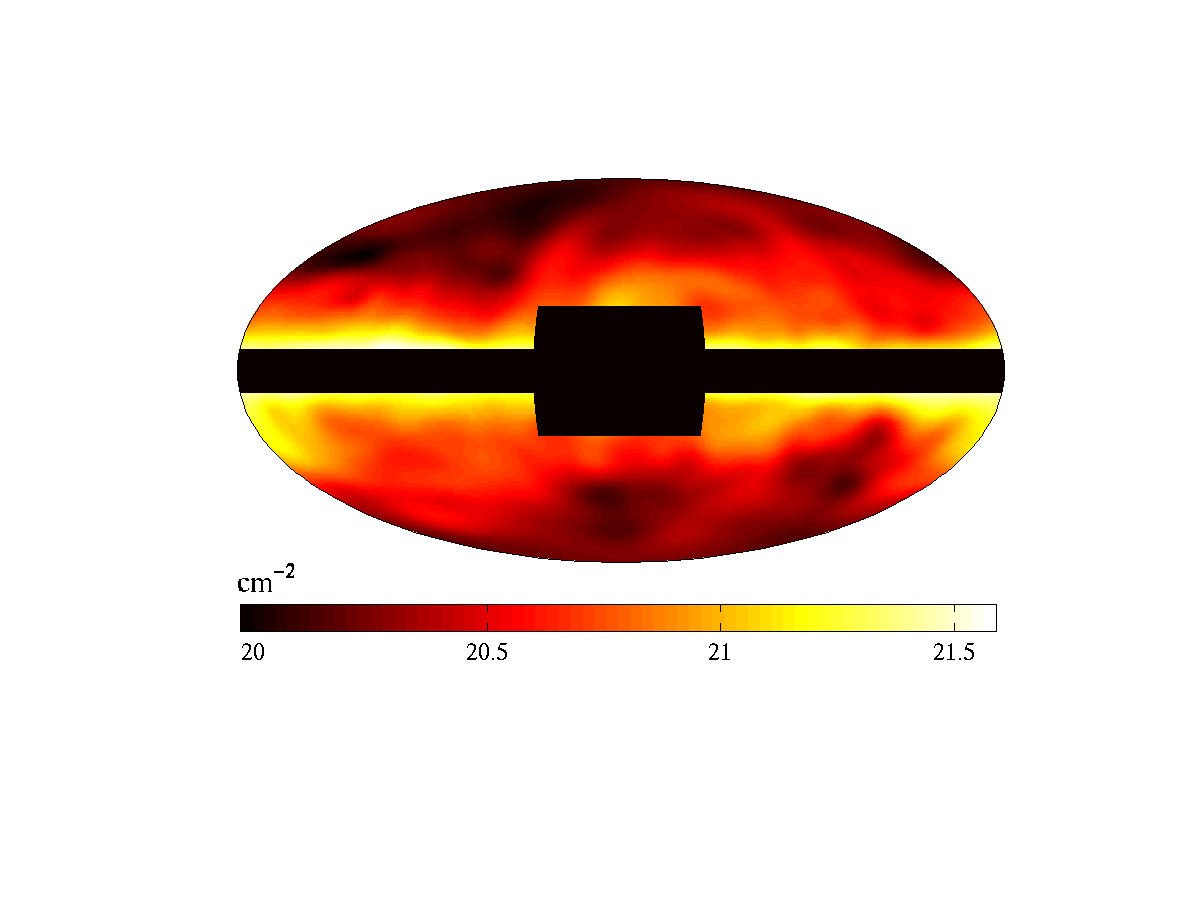
	The diffuse extragalactic backgrounds in γ-rays and in <1GHz radio frequencies are not well-known. The γ-ray sky (left image, from EGRET) shares several features with tracers of our own Galaxy even at high Galactic latitudes (e.g., Hα emission, right image), suggesting that the diffuse emission originates mostly from cosmic-ray interactions within the Milky-Way [credit].
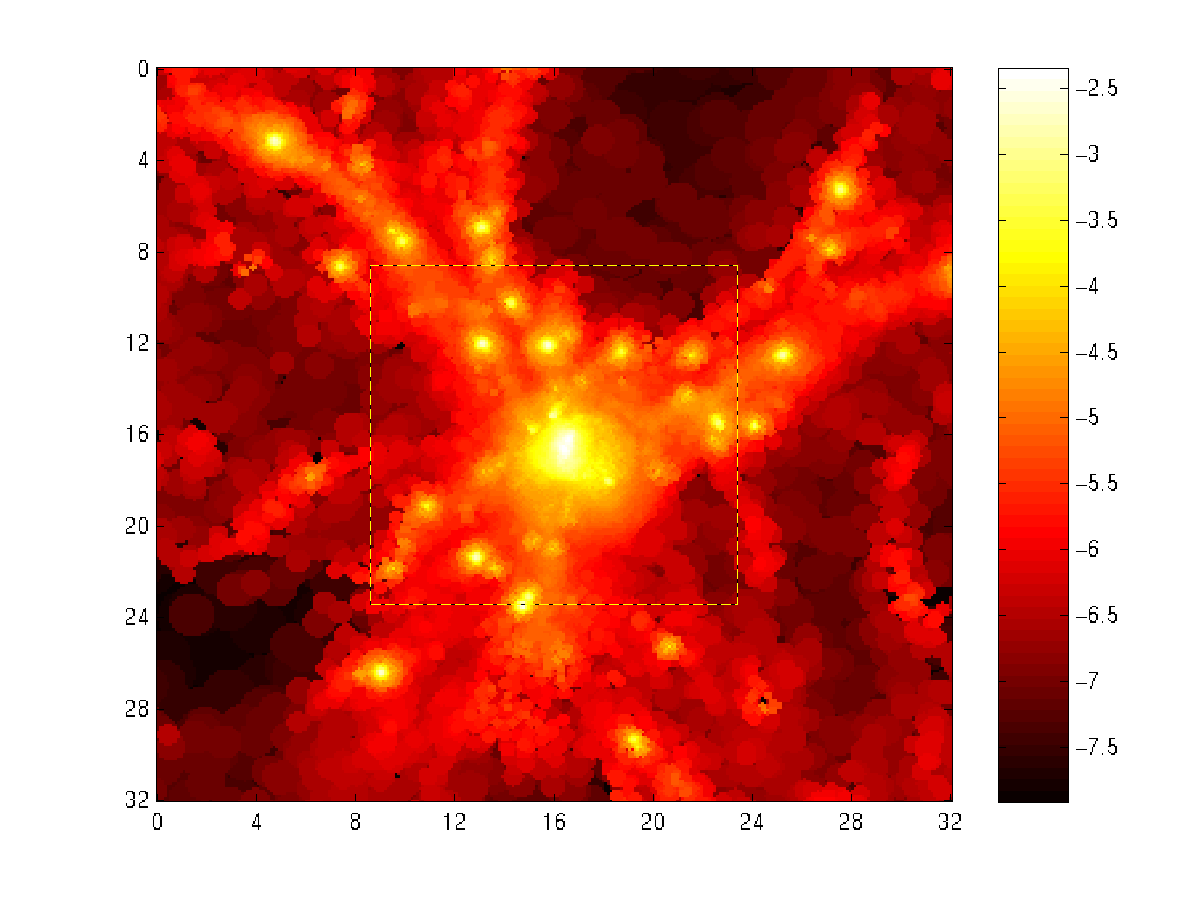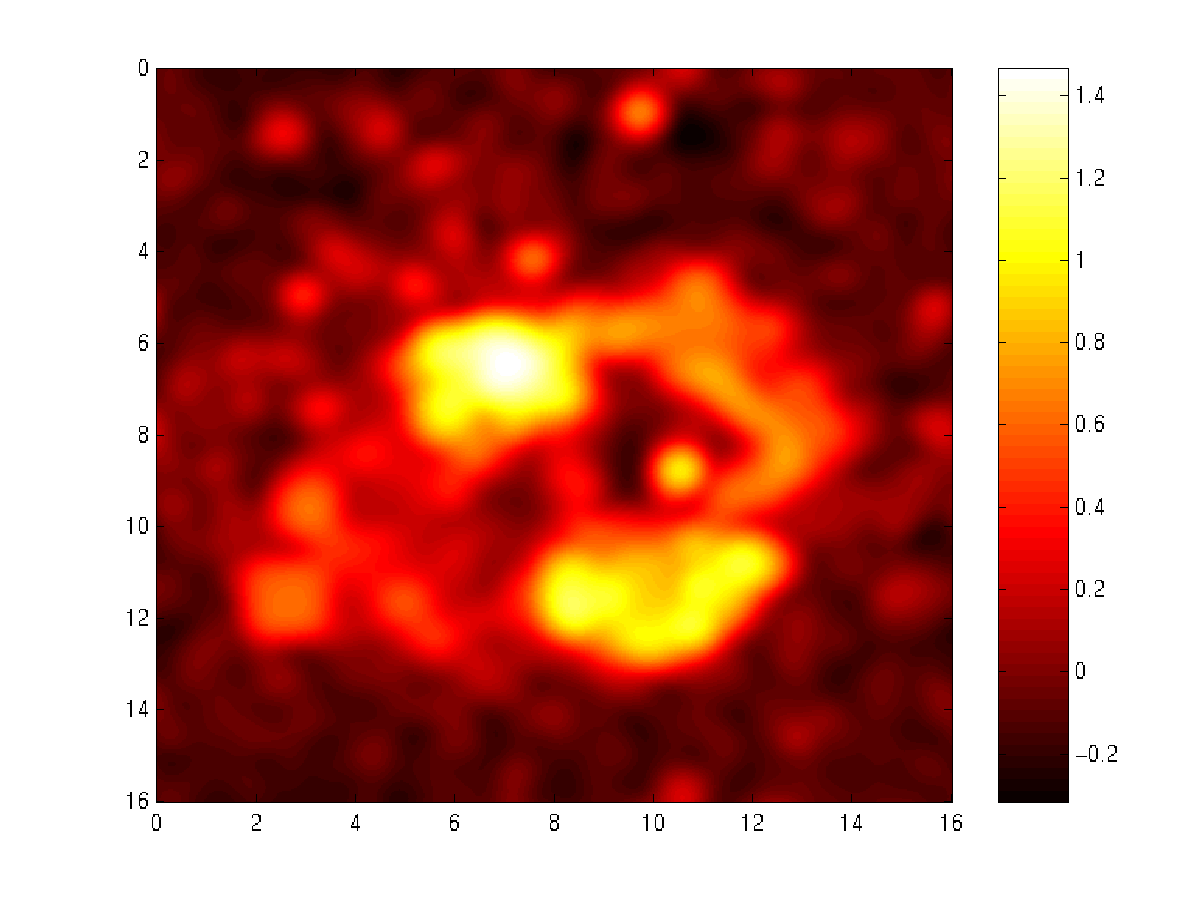
	Large scale accretion shock waves are an inevitable outcome of structure formation in the Universe. These shocks should be observable in γ-rays by the 5-year Fermi mission [1, 2] and in radio [1, 2] by the SKA possible by LOFAR. Preliminary observations in both γ-rays and radio have been reported. Images: simulated galaxy cluster (left: baryon number density) and associated γ-ray emission (right: depicting observed image of the region marked on left) [credit]. (Shocks also occur as galaxy or galaxy clusters collide, see e.g. Stephan's quintet in radio, infrared and x-rays.)
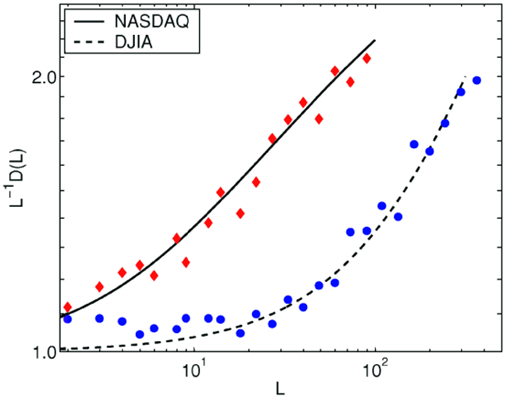
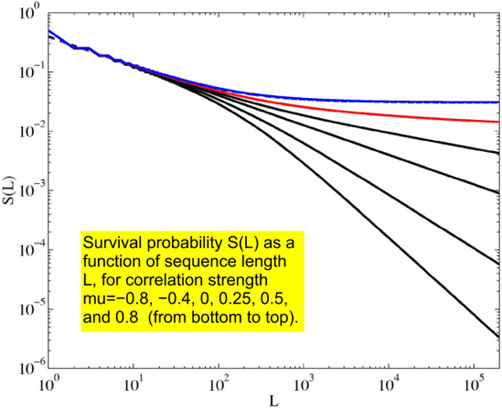
	A wide variety of dynamical systems with long-range correlations can be analyzed in terms of history-dependent random walks. We presented a simple, analytically solvable model for random processes with long-term memory, which exhibits a dynamical phase transition from normal to super-diffusion. The model can be used, for example, to quantify stock market behavior (left plot). A related phase transition from finite to power-law decaying survival probability S(L) is found in the presence of an absorbing barrier (right plot). This describes, for example, an investor's probability to remain in profit at time L.