Phys. Rev. Lett. 95, 136803 (2005)
Quasiparticle Tunneling through a Barrier in the Fractional Quantum Hall Regime
Elad Shopen,1 Yuval Gefen,2 and Yigal Meir1,3
1Department of Physics, Ben-Gurion University, Beer-Sheva 84105, Israel
2Department of Condensed Matter Physics, The Weizmann Institute of Science, Rehovot 76100, Israel
3The Ilse Katz Center for Meso- and Nano-Scale Science and Technology, Ben-Gurion University, Beer-Sheva 84105, Israel
(Received 7 April 2005; published 22 September 2005)
Tunneling of fractionally charged quasiparticles (QPs) through a barrier is considered in the context of a multiply connected geometry. In this geometry global constraints do not prohibit such a tunneling process. The tunneling amplitude is evaluated and the crossover from mesoscopic QP-dominated to electron-dominated tunneling as the system's size is increased is found. The presence of disorder enhances both electron and QP-tunneling rates.
References
For more information on reference linking in this journal, see Reference Sections and Reference Linking in Abstracts.
- R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983).
- S. A. Kivelson and V. L. Pokrovsky, Phys. Rev. B 40, R1373 (1989);
S. Kivelson, Phys. Rev. Lett. 65, 3369 (1990);
J. A. Simmons, H. P. Wei, L. W. Engel, D. C. Tsui, and M. Shayegan, Phys. Rev. Lett. 63, 1731 (1989); [ISI]
J. A. Simmons, S. W. Hwang, D. C. Tsui, H. P. Wei, L. W. Engel, and M. Shayegan, Phys. Rev. B 44, 12 933 (1991); [ISI]
V. J. Goldman and B. Su, Science 267, 1010 (1995). [Inspec] [ISI]
- D. J. Thouless and Y. Gefen, Phys. Rev. Lett. 66, 806 (1991); [ISI]
Y. Gefen and D. J. Thouless, Phys. Rev. B 47, 10 423 (1993); [ISI]
see also Y. Avron, R. Seiler, and B. Shapiro, Nucl. Phys. B265, 364 (1986);
D. J. Thouless, Phys. Rev. B 40, R12034 (1989).
- K. Moon, H. Yi, C. L. Kane, S. M. Girvin, and M. P. A. Fisher, Phys. Rev. Lett. 71, 4381 (1993); [ISI]
M. P. A. Fisher and L. I. Glazman, Mesoscopic Electron Transport, edited by L. Kowenhoven, G. Schoen, and L. Sohn, NATO ASI Series Vol. 345 (Dordrecht, Boston, 1997), p. 331.
- R. de-Picciotto, M. Reznikov, M. Heiblum, V. Umansky, G. Bunin, and D. Mahalu, Nature (London) 389, 162 (1997); [Inspec] [ISI]
L. Saminadayar, D. C. Glattli, Y. Jin, and B. Etienne, Phys. Rev. Lett. 79, 2526 (1997). [ISI]
- E. Comforti, Y. C. Chung, M. Heiblum, and V. Umansky, Nature (London) 416, 515 (2002);
Y. C. Chung, M. Heiblum, and V. Umansky, Phys. Rev. Lett. 91, 216804 (2003).
- J. Martin, S. Ilani, B. Verdene, J. Smet, V. Umansky, D. Mahalu, D. Schuh, G. Abstreiter, and A. Yacoby, Science 305, 980 (2004).
-
Note that only forward scattering is involved here. This means that the
transmission probability is 1, implying the absence of noise in the dc
limit. The noise alluded to above may be detected at finite frequencies.
- B. I. Shklovskii, Pis'ma Zh. Eksp. Teor. Fiz. 36, 43 (1982) [Inspec]
[JETP Lett. 36, 51 (1982)]; [SPIN] [ISI]
Q. Li and D. J. Thouless, Phys. Rev. B 40, 9738 (1989). [ISI]
- For a ridge whose extension in the y direction is Lbarrier, the number of extended holes required to render the ridge dry is Nh=[RLbarrier/
![[script-l]](prl95-136803-2005_files/ell.gif)
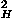 ]+1.
]+1.
- F. D. M. Haldane and E. H. Rezayi, Phys. Rev. B 31, R2529 (1985).
- The total angular momentum is defined mod(N
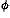 ).
).
- F. D. M. Haldane, Phys. Rev. Lett. 51, 605 (1983);
S. A. Trugman and S. Kivelson, Phys. Rev. B 31, 5280 (1985). [ISI]
-
In the present Letter we employ a numerical recipe for the construction
of extended hole states. We note that these may also be obtained
analytically, starting with Laughlin's state with localized holes. As
this requires some detail, and is not crucial to understanding the
present analysis, we will present it elsewhere. For Nh=1:
 n=
n=![[integral]](prl95-136803-2005_files/int.gif) g
g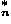 (z0)
(z0) (z0)dz0, where gn's are single-particle states on the extended unit cell 2
(z0)dz0, where gn's are single-particle states on the extended unit cell 2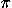 mR×mL, and
mR×mL, and  (z0) is a Laughlin state with a localized hole at z0 11.
(z0) is a Laughlin state with a localized hole at z0 11.
- The width of a single-particle quasimomentum state in the y direction is
![[script-l]](prl95-136803-2005_files/ell.gif) H. When Nh<R/
H. When Nh<R/![[script-l]](prl95-136803-2005_files/ell.gif) H, we have a reduced density rather than a dry area.
H, we have a reduced density rather than a dry area.
- Other forms for V1 lead to similar results.
- A. Auerbach, Phys. Rev. Lett. 80, 817 (1998). [ISI]
- E. Comforti, Y. C. Chung, M. Heiblum, and V. Umansky, Phys. Rev. Lett. 89, 066803 (2002).
- Helias and Pfannkuche (condmat/0403126)


![[script-l]](prl95-136803-2005_files/ell.gif)
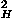 ]+1.
]+1.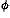 ).
). n=
n=![[integral]](prl95-136803-2005_files/int.gif) g
g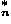 (z0)
(z0) (z0)dz0, where gn's are single-particle states on the extended unit cell 2
(z0)dz0, where gn's are single-particle states on the extended unit cell 2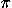 mR×mL, and
mR×mL, and  (z0) is a Laughlin state with a localized hole at z0 11.
(z0) is a Laughlin state with a localized hole at z0 11.![[script-l]](prl95-136803-2005_files/ell.gif) H. When Nh<R/
H. When Nh<R/![[script-l]](prl95-136803-2005_files/ell.gif) H, we have a reduced density rather than a dry area.
H, we have a reduced density rather than a dry area.