Highlights
The lognormal-like statistics of a stochastic squeeze process.- Consider the phase space dynamics near an hyperbolic point. Starting with some initial distribution $\rho(0)$, after some time t, this distribution will be "squeezed". Adding a random rotation to the dynamics, how will the squeezing of $\rho(t)$ be suppressed ? Have a look at The lognormal-like statistics of a stochastic squeeze process for some more info.
Localization due to topological stochastic disorder inactive networks.- A stochastic picture of dynamics is often written as a rate equation $$\dot{\vec{p}} = W \vec{p}$$ Where $W$ is the rate matrix. The rates between any two sites can always be written as $W_{ij} = w_{ij} \exp( \mathcal{E}_{ij})$, where $w$ is symmetric and $\mathcal{E}$ anti-symmetric. The sum $\sum \mathcal{E}$ over some closed path in the network called affinity. It is identically zero for systems in equilibrium, and the eigenvalues of $W$ are real. Here we introduce topological stochastic disorder , which reflects non-uniformity of the affinity in the system. Contrary to the "usual" disorder, this type of disorder makes the spectrum complex. This paper Below is the dynamics of a 2-channel system with non-zero affinity. See Localization due to topological stochastic disorder in active networks .
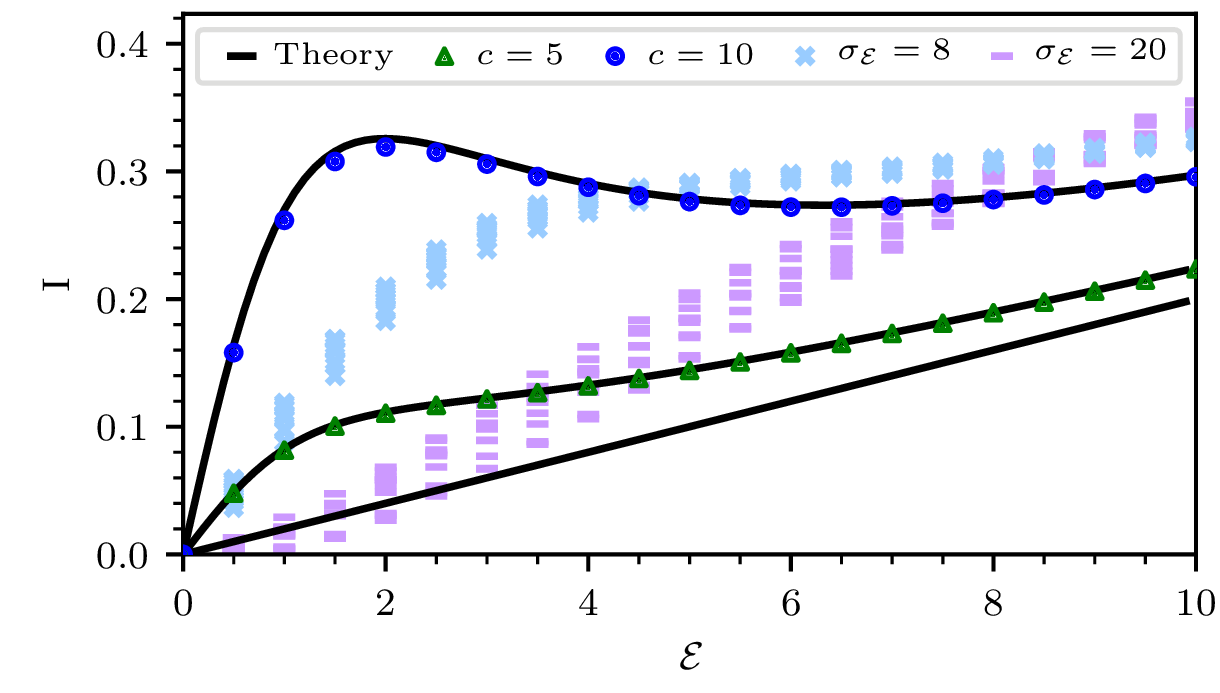
Quantum stochastic transport along chains.-
In this work we consider a quantum particle in tight-binding lattice, in an Ohmic environment.
The particle can hop either due to coherent transitions, arising
from a momentum term $\sim c \cos(\mathbf{p})$ in the Hamiltonian,
or due to stochastic terms, arising from the coupling to the bath.
Because of these two terms, we find that the current is a non-monotonic function
of the bias. The image below shows this non-monotonicity for different values of the hopping $c$.
For more information see here.