Abstract
In spite of extended efforts, detecting thermoelectric effects in superconductors has proven to be a challenging task, due to the inherent superconducting particle-hole symmetry. Here we present a theoretical study of an experimentally attainable Superconductor – Quantum Dot – Superconductor (SC-QD-SC) Josephson Junction. Using Keldysh Green’s functions we derive the exact thermo-phase and thermal response of the junction, and demonstrate that such a junction has highly tunable thermoelectric properties and a significant thermal response. The origin of these effects is the QD energy level placed between the SCs, which breaks particle-hole symmetry in a gradual manner, allowing, in the presence of a temperature gradient, for gate controlled appearance of a superconducting thermo-phase. This thermo-phase increases up to a maximal value of ±π/2 after which thermovoltage is expected to develop. Our calculations are performed in realistic parameter regimes, and we suggest an experimental setup which could be used to verify our predictions.
Introduction
Thermoelectric (TE) effects correspond to the response of electrical charge (via induced current or voltage) when a thermal bias is applied across a junction. Since the warmer side has an equal excess of both particles and holes, the direction and magnitude of the TE response are determined by the asymmetry between particles and holes. Consequently, TE effects have proven to be a powerful tool in probing the density of states near the Fermi energy, particularly in materials with strong electron-electron interactions1,2,3. However, in superconductors (SCs), which are a paradigmatic example of interacting electron systems, the TE response is both small in magnitude and hard to control. This is because SCs are inherently particle-hole (p-h) symmetric, and the p-h asymmetry stems primarily from impurity scattering4,5,6. Measuring a substantial and controllable TE response in SCs is therefore a major challenge.
Early experiments searching for thermocurrent in superconductors found that even the expected small thermocurrent was generally absent7. An explanation for the absence of thermoelectric response was proposed by Ginzburg8, who suggested, within the two fluid scheme, that the superfluid is expected, under certain conditions, to counterbalance the quasi-particle (QP) current with a non-dissipative supercurrent9. The existence of such a supercurrent is accompanied by an induced gradient in the phase of the SC order parameter10,11.
To overcome the absence of current, experiments in which the setup comprises a bi-metallic loop (taking advantage of the fact that the SC phase has to be geometrically quantized), were proposed and performed11,12. However, different experiments13 disagreed with each other and with theory14,15, a discrepancy which only recently may have been resolved16. Suggestions for increasing the thermal response and p-h asymmetry include using magnetic impurities17 or a ferromagnetic junction setup18, leading to a thermo-phase of greater magnitude. However, using a magnetic field for tuning the system parameters19 leads to substantial experimental limitations.
In spite of all these efforts, the challenge of devising a SC system which exhibits substantial TE effects and with a large degree of control is yet to be met. Here, we demonstrate that in a SC-quantum dot (QD)-SC setup (schematically depicted in Fig. 1(a)), the TE response can be considerably larger than in SC tunnel junctions10, where measurable thermo-phase can only arise around the transition temperature. Control over its magnitude can be achieved by a gate voltage, which shifts the energy levels of the QD, allowing for breaking of the p-h symmetry even for ideal SC electrodes, thus enabling experimental control of the magnitude and direction of the thermal response. It is important to note, that such a setup is within current experimental capabilities20,21,22,23, making our predictions experimentally verifiable.
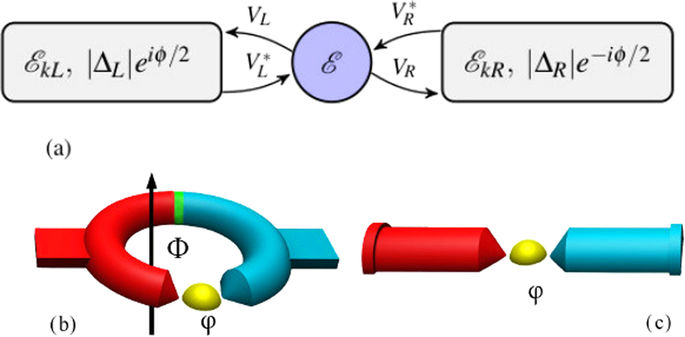
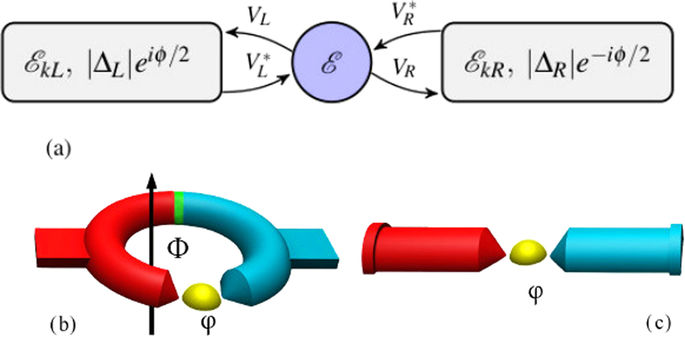
(a) Schematic representation of the SC-QD-SC setup. The two SC leads are characterized by their spectrum, gap energies and their phases. The QD contains a single degenerate level of energy ε. (b) Closed loop experimental setup. In this setup the phase difference Δϕ is geometrically constrained, so it cannot always compensate for the thermal quasi-particle current. (c) Open experimental setup, where Δϕ can assume arbitrary values.
Model
Our model consists of bulk s-type superconductors as leads, with individual gap energies and arbitrary phases (taken symmetrically for convenience), and a single QD level in between. The Hamiltonian for the SC-QD-SC junction is given by H = HL + HR + HQD + HV, with the lead Hamiltonians Hs (s = L, R) given by
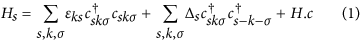
where 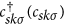 is the creation
(annihilation) of an electron on side s with
momentum k, spin σ. The order
parameter is complex,
is the creation
(annihilation) of an electron on side s with
momentum k, spin σ. The order
parameter is complex, 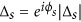 and the phase difference is
taken, without loss of generality, as ϕL
= −ϕR = ϕ/2. The
chemical potential in the SC leads is defined as the
zero of energy. We first start with a
non-interacting, single-level QD. In this case, the
QD Hamiltonian HQD and the
hopping Hamiltonian between the QD and the SCs, HV,
are
and the phase difference is
taken, without loss of generality, as ϕL
= −ϕR = ϕ/2. The
chemical potential in the SC leads is defined as the
zero of energy. We first start with a
non-interacting, single-level QD. In this case, the
QD Hamiltonian HQD and the
hopping Hamiltonian between the QD and the SCs, HV,
are
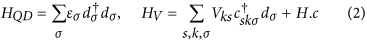
where 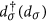 is the creation
(annihilation) of an electron on the dot with spin σ.
While the calculation is quite general, in the
present context we assume spin degeneracy, ε↑
= ε↓ ≡ ε, and uniform
tunneling Vks ≡ Vs.
From this Hamiltonian, the currents and other
quantities are calculated using the non-equilibrium
Green’s function method, as described in the Methods
section.
is the creation
(annihilation) of an electron on the dot with spin σ.
While the calculation is quite general, in the
present context we assume spin degeneracy, ε↑
= ε↓ ≡ ε, and uniform
tunneling Vks ≡ Vs.
From this Hamiltonian, the currents and other
quantities are calculated using the non-equilibrium
Green’s function method, as described in the Methods
section.
Results
We start by addressing the general form of the current. Substituting the Green’s function (Eq. 10 in the Methods section) into the expression for the current, we find that the current can be generally divided into three terms: quasi-particle current, IQP, Josephson (pair) current, Isc, and a term involving pair-QP transition, Ipair−QP,
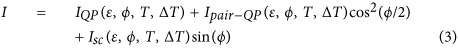
A temperature dependence exists in all the terms through the temperature dependence of the superconducting order parameter. The usefulness of this form for the current stems from the fact that within the relevant parameter range discussed here, the phase dependence of the amplitude of the various current terms is negligible. This phase dependence originates from multiple reflections between the QD and the leads, giving rise to higher harmonic processes with a non trivial phase function. These reflections diminish as a function of Γs/ε, i.e. as the energy level in the QD moves away from the Fermi level, and as a result Cooper pairs have smaller probability of tunneling across the junction. In the parameter range for which the thermo-phase is appreciable – the tunnel junction regime – the ratio Γs/ε is small and thus multiple reflections can practically be neglected.
In an open junction setup (Fig. 1(c)), with no externally imposed constrains over the thermo-phase, the thermally induced current is completely canceled by the appearance of a thermo-phase across the junction8. This serves as the definition for the thermo-phase ϕth:
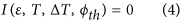
Linear Response
In the linear response regime (linear in ΔT), assuming a symmetric junction, one can write the different terms in Eq. 3 explicitly:
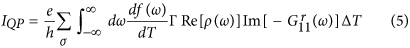
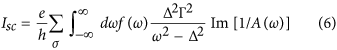
where the parameters Γ and Δ were taken equal on
both sides of the junction. In these equations, the
expression for 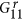 and A, whose
contributions to the current are plotted in Fig.
2, is given by
and A, whose
contributions to the current are plotted in Fig.
2, is given by 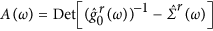 (Fig.
2(a)) and
(Fig.
2(a)) and 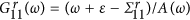 (Fig.
2(b)). The transmission channel for the QPs,
(Fig.
2(b)). The transmission channel for the QPs, 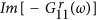 , demonstrates the asymmetry
of transmission as a function of energy, required to
generate a thermoelectric response. On the other
hand, the transmission channel for pairs, 1/A(ω),
is driven by a superconducting phase difference,
generated to compensate for the QP contribution, and
thus does not require p-h asymmetry. As can be seen
in Fig.
2(a,b), both the QP channel and the pair
channel contain sharp resonances which are Andreev
bound states (ABS) (though the ABS do not
participate in the QP transport due to Re[ρ(ω)]
term in Eq. 5, as ρ has a real part only
outside the gap). The pair-QP transition term Ipair−QP
vanishes identically, since this thermal transport
process is perfectly particle-hole symmetric
(mathematically, writing Ipair−QP
as an integral similar to Eq. 5, the integrand is an
odd function of ω, as a result of a
symmetric transmission channel in this process).
, demonstrates the asymmetry
of transmission as a function of energy, required to
generate a thermoelectric response. On the other
hand, the transmission channel for pairs, 1/A(ω),
is driven by a superconducting phase difference,
generated to compensate for the QP contribution, and
thus does not require p-h asymmetry. As can be seen
in Fig.
2(a,b), both the QP channel and the pair
channel contain sharp resonances which are Andreev
bound states (ABS) (though the ABS do not
participate in the QP transport due to Re[ρ(ω)]
term in Eq. 5, as ρ has a real part only
outside the gap). The pair-QP transition term Ipair−QP
vanishes identically, since this thermal transport
process is perfectly particle-hole symmetric
(mathematically, writing Ipair−QP
as an integral similar to Eq. 5, the integrand is an
odd function of ω, as a result of a
symmetric transmission channel in this process).
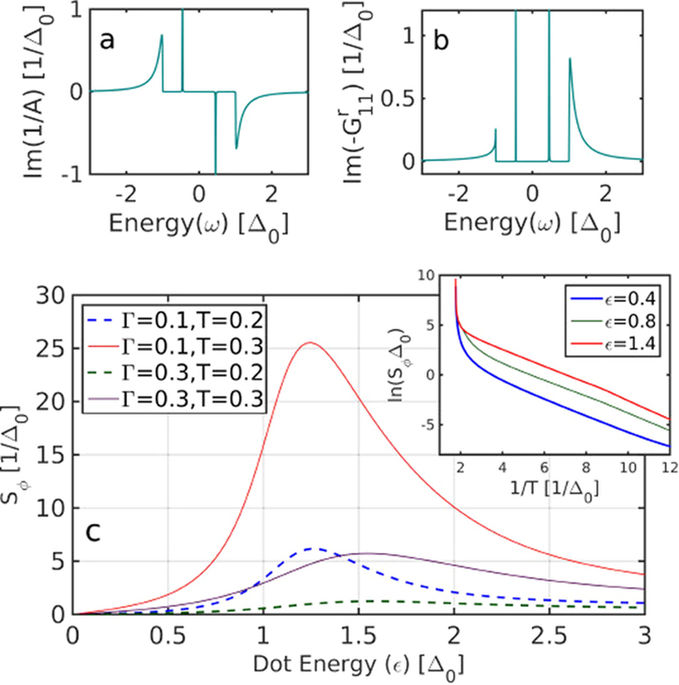
(a) Imaginary part of 1/A, the pair
channel of transmission through the dot, as
a function of energy, for Γ = 0.1,ε =
0.5,ϕ = π/2. The narrow
peaks are the ABS inside the gap (b)
Imaginary part of 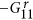 , the quasi-particle
channel of transmission through the dot,
which is proportional to the DOS of
electrons on the dot, as a function of
energy, for the same parameters as (a). The
p-h asymmetry is visible in the continuum. (c)
The thermo-phase Seebeck coefficient Sϕ
(Eq. 7) as a function of dot energy, for
various T and Γ. The peak position
depends only on Γ and Δ as will be discussed
in the text. Inset: ln(Sϕ)
as a function of inverse temperature for
various dot levels, ε = 0.4, 0.8,
1.4.
, the quasi-particle
channel of transmission through the dot,
which is proportional to the DOS of
electrons on the dot, as a function of
energy, for the same parameters as (a). The
p-h asymmetry is visible in the continuum. (c)
The thermo-phase Seebeck coefficient Sϕ
(Eq. 7) as a function of dot energy, for
various T and Γ. The peak position
depends only on Γ and Δ as will be discussed
in the text. Inset: ln(Sϕ)
as a function of inverse temperature for
various dot levels, ε = 0.4, 0.8,
1.4.
Since in linear response one can define I = σΔϕ + SϕσΔT, in analogy to the Seebeck coefficient, we can define the thermo-phase Seebeck coefficient (TPSC) in a similar manner,
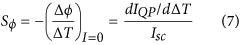
In Fig.
2(c), the TPSC Sϕ is
plotted as a function of dot level energy ε,
for various temperatures T and couplings Γ.
Sϕ consistently peaks
around |ε| = Δ + aΓ, with the factor a
being typically a ~ 1–2.5 for the relevant
parameters (Γ > 0.05). The TPSC peak occurs when
the dot energy is slightly above the SC coherence
peaks in the BCS DOS, at the point that maximizes
the interplay of p-h asymmetry and transmission.
This is similar in nature to the Seebeck coefficient
peak through a QD between normal leads24,
which resides a distance Γ above (or below) the QD
energy level resonance. In the inset of Fig.
2(c) we plot the inverse temperature
dependence of the TPSC on a log scale, for various
level energies. For T ≪ Δ the leading
contribution to the temperature dependence of the
TPSC stems from the activated form of the the Fermi
function in the QP term (5), which can be
approximated by 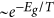 , where Eg
is an activation energy. Indeed, the logarithmic
slopes of Sϕ, depicted in
the inset of Fig.
2(c), are linear with an activation gap Δ0,
as expected for QPs. This description works rather
well for most of the relevant temperature range. In
the opposite limit, for T approaching the SC
transition temperature Tc,
the TPSC diverges due to vanishing of the Josephson
term, as 1/Δ2 ~ (T − Tc)−1.
, where Eg
is an activation energy. Indeed, the logarithmic
slopes of Sϕ, depicted in
the inset of Fig.
2(c), are linear with an activation gap Δ0,
as expected for QPs. This description works rather
well for most of the relevant temperature range. In
the opposite limit, for T approaching the SC
transition temperature Tc,
the TPSC diverges due to vanishing of the Josephson
term, as 1/Δ2 ~ (T − Tc)−1.
Beyond Linear Response
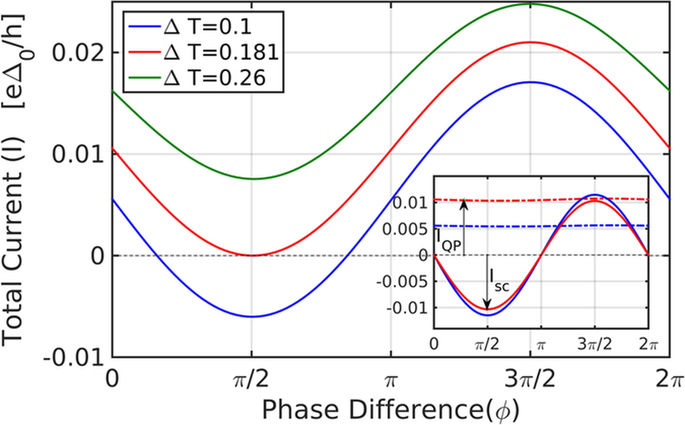
The formulation described in the previous section applies, in fact, also beyond the linear response regime in ΔT, where the main deviation from linear response stems from the difference in order parameters on both sides due to thermal difference. The full analytical expression, including all contributions, is quite long and thus will not be shown here. Figure 3 depicts the total current as a function of phase for several values of temperature difference, ΔT. The general division of the current into the three terms (Eq. 3) holds also beyond the linear response regime, as can be seen in the inset of Fig. 3, which shows the QP and the Josephson contributions to the total current (the contribution from the pair-QP transition term Ipair−QP still vanishes). The Josephson term is modified due the difference in Δ between the two sides25. As can be clearly seen from the figure, the QP term is almost insensitive to phase difference, but sensitive to changes in temperature difference, while the Josephson term oscillates with the phase difference, but weakly sensitive to temperatures far from the SC transition temperature.
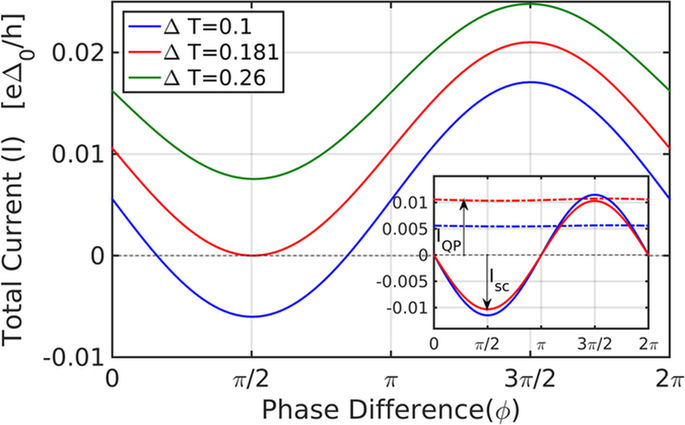
Inset: current divided into the two contributions: quasi-particle current and Josephson current. The first (QP) term in eq. (3) gives the up shift in current due to temperature bias and the third (Josephson) term gives the amplitude of the modulation with phase. Phase dependence is negligible in the QP term (dot-dashed line).
As the temperature difference increases beyond a critical value ΔTc (the red curve in Fig. 3, corresponding to ΔT = 0.181 for the depicted set of parameters) the QP current reaches a value such that the Josephson current can no longer compensate for it (for ΔT = ΔTc the thermo-phase is exactly ±π/2). If the total current is kept at zero, an effective voltage will develop in this regime, which will give rise to a time-dependent AC response (as in the AC Josephson effect), an effect which has in fact been measured in tunnel junctions26. We leave the time-dependent thermal Josephson effect for a future study, and concentrate here on ΔT below the critical value ΔTc.
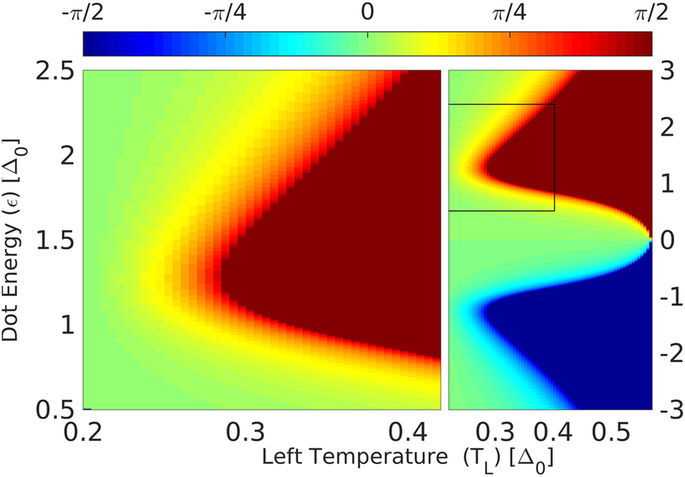
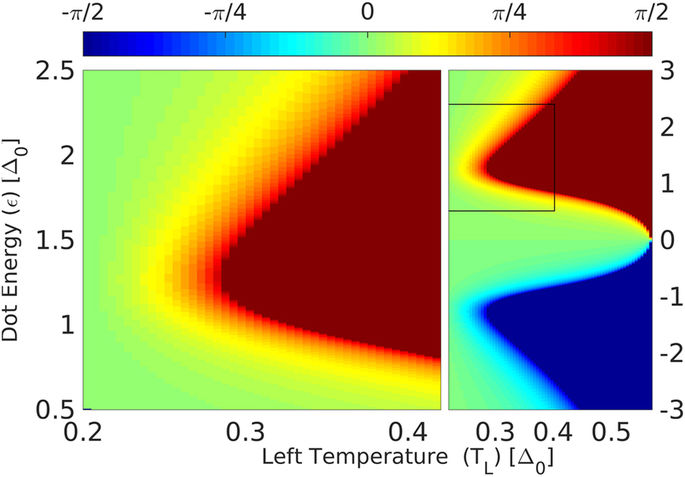
Solving the condition (4) for vanishing current, we plot in Fig. 4 the thermo-phase ϕth as a function of the left lead temperature TL (for fixed TR) and QD level energy ε. The region of ϕth = ±π/2 (red or blue plateau in Fig. 4) corresponds to the regime for which ΔT ≥ ΔTc, and is not covered in this work. The value of the critical temperature difference as a function of dot energy can be read from Fig. 4 as the contour of the ±π/2 plateau. The value of the critical ΔTc can be directly measured in experiments, by applying a temperature difference and monitoring for which ΔT a finite current (or voltage) begins to appear.
Coulomb Interaction
So far we have ignored the on-site interaction on
the QD, which may be important, for example, in the
Coulomb blockade regime27.
In order to address this, we add to the Hamiltonian
an on-site Coulomb interaction, represented by a
term HU = Un↑n↓,
where 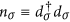 . Within the Hartree-Fock
(HF) approximation, the dot levels are renormalized
according to
. Within the Hartree-Fock
(HF) approximation, the dot levels are renormalized
according to 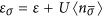 , where the dot occupations
〈nσ〉 are calculated
self-consistently (
, where the dot occupations
〈nσ〉 are calculated
self-consistently (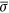 is the spin opposite to σ).
Once the dot levels and occupations are determined
(inset in Fig.
5), the thermo-phase can be calculated using
Eq. 4.
is the spin opposite to σ).
Once the dot levels and occupations are determined
(inset in Fig.
5), the thermo-phase can be calculated using
Eq. 4.
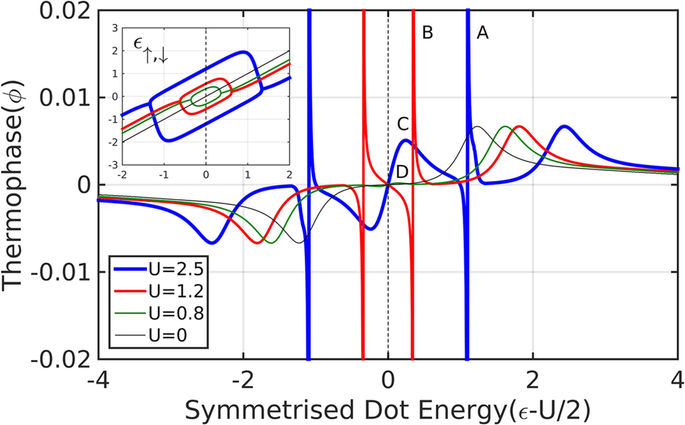
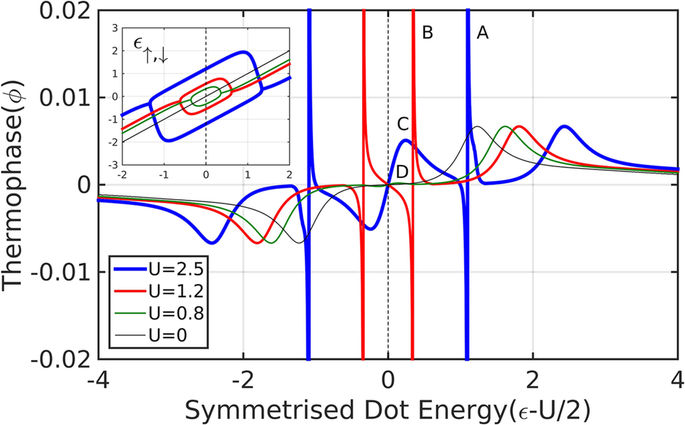
Compared to the non-interacting problem, the interaction introduces a new regime where the dot is singly occupied, the effective spin energy levels split28, and a magnetic moment forms. This splitting suppresses the pair tunneling amplitude, where eventually the Josephson term becomes smaller and, unless smeared by temperature, changes sign, leading to a π-junction transition29,30. It is important to note that the HF approximation, while found to generally describe the SC-QD-SC physics very well29,31, will not be valid in the Kondo regime, where Tk > Δ32. In addition, it may give qualitatively inaccurate values for the boundaries of the singly occupied regime33. These failures of the HF approximation are rather limited in the small Γ/Δ limit33, which is the regime of interest in the present work, and therefore we can safely proceed with its usage. Furthermore, we note that although there seems to be an apparent spin symmetry breaking from the form of the HF solution, these spin-asymmetric solutions are doubly-degenerate with the degenerate solutions having opposite spins. It is thus important to take both solutions into account to preserve spin symmetry. In Fig. 5 we show the thermo-phase ϕth as a function of the bare dot energy (shifted by half the Coulomb interaction), for various values of U. We first note that the thermo-phase is symmetric not around ε = 0, but around the new (and only) point of particle-hole symmetry, ε − U/2 = 0. There are other points, inside the singly occupied region, where the QP term (and consequently also the thermo-phase) vanish, but this is due to cancellation of contributions and not because of p-h symmetry. Inside this region, we also see sharp ±π/2 peaks (points A, B in Fig. 5) which correspond to a vanishing Josephson term during the π-junction transition, where any thermal gradient will produce the maximal thermo-phase of ±π/2. Other new features (such as a small peak at point C and a tiny peak at point D in Fig. 5) emerge from the non-monotonous behavior of the QP term, in the singly occupied regime. In this regime, the contributions from the two spin levels have opposite signs and their magnitude difference also changes sign as a function of average dot energy. The features outside this region, however, are unaffected by the interaction except for the trivial shift away from the p-h symmetry point by U/2.
Discussion
All the results presented in this paper can be directly tested experimentally. To measure the thermoelectric effect and the thermo-phase, we suggest the experimental setup depicted in Fig. 1(b). It consists of a SC ring with one branch including a QD while the other branch including a thin insulating barrier. One side of the ring is heated in order to create a temperature gradient, and as a result, a unidirectional circulating thermocurrent arises. This setup makes use of the geometrical constraint on the gauge invariant phase, and of the fact that the phase drop occurs primarily at the point of most resistance34 (which is the QD as opposed to the insulating barrier). This implies that the phase difference across the QD junction is ϕ = 2π(Φ/Φ0 + n), where Φ is the magnetic flux penetrating the ring and Φ0 = hc/2e is the flux quantum. Since there is no external magnetic flux, the phase difference across the QD, necessary to produce the supercurrent that cancels the thermal current in the bulk of the SC, is accompanied by a generation of a magnetic flux through the ring. This flux, in fact, arises from supercurrents running on the surface of the ring12. This experimentally measurable flux can be continuously modified by the applied temperature gradient, or the position of the dot level energy. In order to measure the critical temperature difference, an open setup (Fig. 1(c)) can also be utilized (where no phase detection is necessary). The temperature difference for which effective thermovoltage begins to appear, is the critical temperature difference. Ref. 22 has already applied setups that involve SCs and a QD, while ref. 21 has already demonstrated applying a temperature bias in SC21, but these two approaches have yet to be experimentally explored together.
In summary, we have demonstrated that a superconductor - quantum dot - superconductor junction can serve as a model system to study thermoelectric effects in SC systems, as it exhibits a large and controllable TE response. The current response to a temperature difference has been studied as a function of the most important control parameters, namely temperature, gate voltage and dot-electrode couplings. Specific experimental realizations to test our predictions have been suggested, and we believe that they are well within current experimental capabilities. Further studies that examine the AC thermal Josephson effect (beyond the critical temperature difference) are currently under way.
Methods
In order to find the current across the junction we
calculate the Green’s function in Nambu space30,
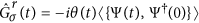 , where
, where 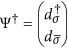 is the Nambu particle-hole
spinor. We find the relevant self energies using the
equations of motion, in Nambu space:
is the Nambu particle-hole
spinor. We find the relevant self energies using the
equations of motion, in Nambu space:
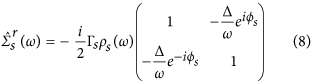
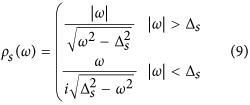
where 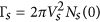 , Ns(0)
being the normal metal density of states (DOS). ρs
can be regarded as the generalized DOS in the
superconductor, normalized by the normal metal
value, where there is an imaginary (|ω| <
Δs) contribution from inside the
gap. Applying the self energies to the Dyson
equation30
we find the retarded Green’s Function in Fourier
space
, Ns(0)
being the normal metal density of states (DOS). ρs
can be regarded as the generalized DOS in the
superconductor, normalized by the normal metal
value, where there is an imaginary (|ω| <
Δs) contribution from inside the
gap. Applying the self energies to the Dyson
equation30
we find the retarded Green’s Function in Fourier
space 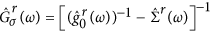 , where
, where
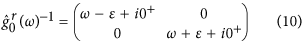
and 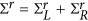 . Using
. Using 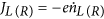 , we express the current in
terms of the Green’s functions on the dot35,
, we express the current in
terms of the Green’s functions on the dot35,
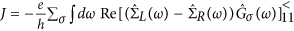 , where the lesser Green’s
functions
, where the lesser Green’s
functions 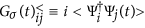 , and we can calculate the
term in the square brackets in the expression for J
using the Langreth relation36
[A(ω)B(ω)]<
= Ar(ω)B<
(ω) + A< (ω)Ba(ω).
, and we can calculate the
term in the square brackets in the expression for J
using the Langreth relation36
[A(ω)B(ω)]<
= Ar(ω)B<
(ω) + A< (ω)Ba(ω).
From a numerical perspective, a broadening of the superconducting gap energy is required to avoid divergence of the superconducting DOS. A suitable Dynes Broadening37,38 is required, and if done carefully (the broadening should be mutually conjugate for particles and holes, namely Δ(ω) = Δ0 − i sign(ω)η), it enables one to directly see the contribution from the Andreev bound states28,30, which are usually numerically elusive (being ideally a delta function contribution to the local DOS), as can be seen in Fig. 2(a,b). In all the calculations the zero temperature SC order parameter on both sides was set as the unit energy, Δs(T = 0) ≡ Δ0 = 1, and all other energy values are measured in units of Δ0. The value of the Dynes broadening parameter used in our calculations is η = 10−4, but the results are largely independent of this value.
Additional Information
How to cite this article: Kleeorin, Y. et al. Large Tunable Thermophase in Superconductor–Quantum Dot–Superconductor Josephson Junctions. Sci. Rep. 6, 35116; doi: 10.1038/srep35116 (2016).
References
- 1.
Behnia, K., Jaccard, D. & Flouquet, J. On the thermoelectricity of correlated electrons in the zero-temperature limit. Journal of Physics: Condensed Matter 16, 5187 (2004).
- 2.
Kim, K.-S. & Pépin, C. Thermopower as a signature of quantum criticality in heavy fermions. Phys. Rev. B 81, 205108 (2010).
- 3.
Zlatić, V., Monnier, R., Freericks, J. K. & Becker, K. W. Relationship between the thermopower and entropy of strongly correlated electron systems. Phys. Rev. B 76, 085122 (2007).
- 4.
Kon, L. Thermoelectric effect in superconductors with nonmagnetic localized states. Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki 70, 286–91 (1976).
- 5.
Gal’Perin, Y. M., Gurevich, V. & Kozub, V. Acoustoelectric and thermoelectric effects in superconductors. Soviet Journal of Experimental and Theoretical Physics Letters 17, 476 (1973).
- 6.
Gal’Perin, Y. M., Gurevich, V. & Kozub, V. Nonlinear acoustic effects in superconductors. Soviet Journal of Experimental and Theoretical Physics 38, 517 (1974).
- 7.
Falco, C. M. & Garland, J. C. Thermoelectric effects in superconductors. In Nonequilibrium Superconductivity, Phonons, and Kapitza Boundaries 521–540 (Springer, 1981).
- 8.
Ginzburg, V. On thermoelectric phenomena in superconductors. J. Phys. USSR 8, 148–156 (1944).
- 9.
Schon, G. Thermoelectric effects in superconductors. In Festkoperprobleme (Advances in Solid State Physics vol. 21, 341 (Vieweg, Braunschweig, 1981).
- 10.
Guttman, G. D., Nathanson, B., Ben-Jacob, E. & Bergman, D. J. Thermoelectric and thermophase effects in Josephson junctions. Phys. Rev. B 55, 12691–12700 (1997).
- 11.
Smith, A. D., Tinkham, M. & Skocpol, W. J. New thermoelectric effect in tunnel junctions. Phys. Rev. B 22, 4346–4354 (1980).
- 12.
Garland, J. & Harlingen, D. V. Thermoelectric generation of flux in a bimetallic superconducting ring. Physics Letters A 47, 423–424 (1974).
- 13.
Zavaritskii, N. V. Observation of superconducting current excited in a superoonducior by heat flow. Soviet Journal of Experimental and Theoretical Physics Letters 19, 126–128 (1974).
- 14.
Artemenko, S. N. & A. V. The thermoelectric field in superconductors. Soviet Journal of Experimental and Theoretical Physics 43, 548 (1976).
- 15.
Galperin, Y. M., Gurevich, V. L., Kozub, V. I. & Shelankov, A. L. Theory of thermoelectric phenomena in superconductors. Phys. Rev. B 65, 064531 (2002).
- 16.
Shelly, C. D., Matrozova, E. A. & Petrashov, V. T. Resolving thermoelectric paradox in superconductors. ArXiv e-prints 1508.07249 (2015).
- 17.
Kalenkov, M. S., Zaikin, A. D. & Kuzmin, L. S. Theory of a large thermoelectric effect in superconductors doped with magnetic impurities. Phys. Rev. Lett. 109, 147004 (2012).
- 18.
Giazotto, F., Heikkilä, T. T. & Bergeret, F. S. Very large thermophase in ferromagnetic Josephson junctions. Phys. Rev. Lett. 114, 067001 (2015).
- 19.
Ozaeta, A., Virtanen, P., Bergeret, F. S. & Heikkilä, T. T. Predicted very large thermoelectric effect in ferromagnet-superconductor junctions in the presence of a spin-splitting magnetic field. Phys. Rev. Lett. 112, 057001 (2014).
- 20.
Roddaro, S. et al. Large thermal biasing of individual gated nanostructures. Nano Research 7, 579–587 (2015).
- 21.
Fornieri, A., Blanc, C., Bosisio, R., D’Ambrosio, S. & Giazotto, F. Nanoscale phase engineering of thermal transport with a Josephson heat modulator. Nat Nano advance online publication (2015) Letter.
- 22.
De Franceschi, S., Kouwenhoven, L., Schonenberger, C. & Wernsdorfer, W. Hybrid superconductor-quantum dot devices. Nat Nano 5, 703–711 (2010).
- 23.
van Dam, Jorden A., Nazarov, Yuli V., Bakkers, Erik P. A. M., De Franceschi, Silvano & Kouwenhoven, Leo P. Supercurrent reversal in quantum dots. Nature 442, 667–670 (2006).
- 24.
Dubi, Y. & Di Ventra, M. Colloquium: Heat flow and thermoelectricity in atomic and molecular junctions. Rev. Mod. Phys. 83, 131–155 (2011).
- 25.
Chang, L.-F. & Bagwell, P. F. Ballistic Josephson-current flow through an asymmetric superconductor21normal-metal21superconductor junction. Phys. Rev. B 49, 15853–15863 (1994).
- 26.
Panaitov, G., Ryazanov, V., Ustinov, A. & Schmidt, V. Thermoelectric ac Josephson effect in {SNS} junctions. Physics Letters A 100, 301–303 (1984).
- 27.
Anderson, P. W. Localized magnetic states in metals. Phys. Rev. 124, 41–53 (1961).
- 28.
Meng, T., Florens, S. & Simon, P. Self-consistent description of andreev bound states in Josephson quantum dot devices. Phys. Rev. B 79, 224521 (2009).
- 29.
Rozhkov, A. V. & Arovas, Daniel P. Josephson Coupling through a Magnetic Impurity. Phys. Rev. Lett. 82, 2788–2791 (1999).
- 30.
Zhu, Y., feng Sun, Q. & han Lin, T. Andreev bound states and the pi-junction transition in a superconductor/quantum-dot/superconductor system. Journal of Physics: Condensed Matter 13, 8783 (2001).
- 31.
Martín-Rodero, A. & Levy Yeyati, A. The Andreev states of a superconducting quantum dot: mean field versus exact numerical results. Journal of Physics: Condensed Matter 24, 385303 (2012).
- 32.
Žonda, M., Pokorný, V., Janiš, V. & Novotný, T. Perturbation theory of a superconducting 0 - π impurity quantum phase transition. Scientific Reports 5, 8821 (2015).
- 33.
Ambegaokar, V. & Baratoff, A. Tunneling between superconductors. Phys. Rev. Lett. 10, 486–489 (1963).
- 34.
Meir, Y. & Wingreen, N. S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 68, 2512–2515 (1992).
- 35.
Haug, H., Jauho, A.-P. & Cardona, M. Quantum kinetics in transport and optics of semiconductors vol. 2 (Springer, 2008).
- 36.
Dynes, R. C., Garno, J. P., Hertel, G. B. & Orlando, T. P. Tunneling study of superconductivity near the metal-insulator transition. Phys. Rev. Lett. 53, 2437–2440 (1984).
- 37.
Mitrović, B. & Rozema, L. A. On the correct formula for the lifetime broadened superconducting density of states. Journal of Physics: Condensed Matter 20, 015215 (2008).
- 38.
Clerk, A. A. & Ambegaokar, V. Loss of π-junction behavior in an interacting impurity Josephson junction. Phys. Rev. B 61, 9109–9112 (2000).
Acknowledgements
We thank M. Di Ventra and O. Entin-Wohlman for illuminating discussions. YM acknowledges support from ISF under grants 11/11 and 292/15. FG acknowledges the European Research Council under the European Union’s Seventh Framework Program (FP7/2007-2013)/ERC Grant agreement No. 615187-COMANCHE for partial financial support.
Author information
Affiliations
-
Department of Physics, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
- Yaakov Kleeorin
- & Yigal Meir
-
The Ilse Katz Institute for Nanoscale Science and Technology, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
- Yigal Meir
- & Yonatan Dubi
-
NEST Istituto Nanoscienze-CNR and Scuola Normale Superiore, I-56127 Pisa, Italy
- Francesco Giazotto
-
Department of Chemistry, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
- Yonatan Dubi
Authors
-
Search for Yaakov Kleeorin in:
-
Search for Yigal Meir in:
-
Search for Francesco Giazotto in:
-
Search for Yonatan Dubi in:
Contributions
F.G. and Y.D. initiated the project. Y.K. performed the analytical and numerical calculations. All authors discussed the results and participated in writing the manuscript.
Competing interests
The authors declare no competing financial interests.
Corresponding authors
Correspondence to Yaakov Kleeorin or Yonatan Dubi.
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
This
work is licensed under a Creative Commons Attribution 4.0
International License. The images or other third party
material in this article are included in the article’s
Creative Commons license, unless indicated otherwise in
the credit line; if the material is not included under the
Creative Commons license, users will need to obtain
permission from the license holder to reproduce the
material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/