Abstract
The influence of static disorder on a quantum phase transition (QPT) is a fundamental issue in condensed matter physics. As a prototypical example of a disorder-tuned QPT, the superconductor–insulator transition (SIT) has been investigated intensively over the past three decades, but as yet without a general consensus on its nature. A key element is good control of disorder. Here, we present an experimental study of the SIT based on precise in-situ tuning of disorder in dual-gated bilayer graphene proximity-coupled to two superconducting electrodes through electrical and reversible control of the band gap and the charge carrier density. In the presence of a static disorder potential, Andreev-paired carriers formed close to the Fermi level in bilayer graphene constitute a randomly distributed network of proximity-induced superconducting puddles. The landscape of the network was easily tuned by electrical gating to induce percolative clusters at the onset of superconductivity. This is evidenced by scaling behavior consistent with the classical percolation in transport measurements. At lower temperatures, the solely electrical tuning of the disorder-induced landscape enables us to observe, for the first time, a crossover from classical to quantum percolation in a single device, which elucidates how thermal dephasing engages in separating the two regimes.
Introduction
The superconductor–insulator transition1,2 (SIT) in disordered two-dimensional (2D) superconductors exhibits a zero-temperature separatrix between the superconducting and insulating phases3,4. The associated scaling behavior5,6 reveals the intrinsic nature of the quantum criticality. Cooper pairs exist even in the insulating phase, which is evidenced by direct observations of the superconducting gap7,8, as well as the earlier observation of a giant magnetoresistance4,9, magneto-oscillations10, and superfluid correlations11. These observations strongly suggest that the loss of pair coherence due to disorder drives the SIT. Several underlying mechanisms for the SIT have been suggested1, including the dirty boson picture based on Anderson localization of Cooper pairs12, classical13 and quantum percolation14 of superconducting clusters.
In the dirty boson model5,12, which assumes that fluctuations of the pair amplitude are negligible, phase fluctuation of the superconducting order parameter destroys global superconductivity. However, some recent reports have pointed out that strong disorder induces amplitude fluctuations to form superconducting islands in the insulating phases, even in homogenously disordered thin films7,15,16,17,18 (which is also relevant to the Higgs amplitude mode19,20). These amplitude fluctuations may drive the universality class of the SIT from the disordered boson class to a percolation universality class, governed by the loss of global connection of disordered superconducting islands.
This issue, concerning the interplay between disorder and superconductivity, is underscored by recent experiments, which have reported classical or quantum percolation critical behavior at the SIT in systems with varying degrees of disorder21,22. The relevance of these two different transitions, classical and quantum percolation, which are governed by different critical exponents, is determined by the question14 whether percolating clusters are formed between superconducting islands via either superconducting paths carrying phase-disrupting currents (classical percolation) or via coherent quantum-tunneling links (quantum percolation). Thus, precise control of disorder is crucial to elucidate the interplay between disorder and thermal dephasing, which is responsible for the classical-to-quantum crossover behaviors, and in particular, to differentiate the disorder-induced geometrical effects on the SIT from generic density modulations.
Varying the thickness1,3 of or annealing23 superconducting thin films has been adopted in previous experiments to change the level of disorder. However, this can result in variations in the carrier density as well as the disorder landscape in a non-controllable way. Electrostatic gating has also been employed for 2D superconducting systems as a means of controlling the carrier density while preserving the spatial disorder on an atomic scale in superconducting films24, heterostructures of complex oxides25, high-Tc superconductor26, and graphene27. Here, we utilize electrostatic gating for accurate and reversible tuning of the disorder-induced landscape at energies close to the Fermi level by modulating both the carrier density and the band gap independently, rather than simple carrier density modulation with an uncontrolled fixed disorder.
Compared with deeply buried 2D electronic systems of semiconducting heterostructures or oxide interfaces, graphene is more chemically inert and easily accessible using contact probes. However, the carriers are not strongly localized in monolayer graphene (MLG), even at the charge-neutral point (CNP), where the nominal carrier density vanishes. This is accounted for by the presence of electron–hole puddles28,29 produced by the disorder potential arising from charged defects on the substrate and/or chemical residues introduced during device fabrication. Since MLG has zero band gap, sufficiently doped bipolar conducting puddles may touch each other [Fig. 1(a)], making the boundaries transmissible by carriers via Klein tunneling. In contrast, in bilayer graphene (BLG), a band gap Eg opens when an electric field is applied perpendicular to the graphene, separating the charged puddles [Fig. 1(b)], and the transport behavior becomes percolative. This feature of BLG allows a high degree of independent control of both the band gap and the carrier density in a wide range30, as shown in Fig. 1(c), and provides flexibility in designing novel devices with controlled conductive behavior by fine-tuning the distance between puddles. Normal percolative transport has been reported in 2D electron gas systems in the low-carrier-density regime31, and in MLG nanoribbons with a finite band gap close to the CNP32. Similar behavior was observed in this study for the gapped BLG with normal electrodes (see Materials and Methods). As the Andreev-paired carriers were induced by the proximity effect in our dual-gated BLG device, the system precisely simulates a percolative SIT via the puddles of the pairs, the geometry of which is determined by disorder tuning at the Fermi level.
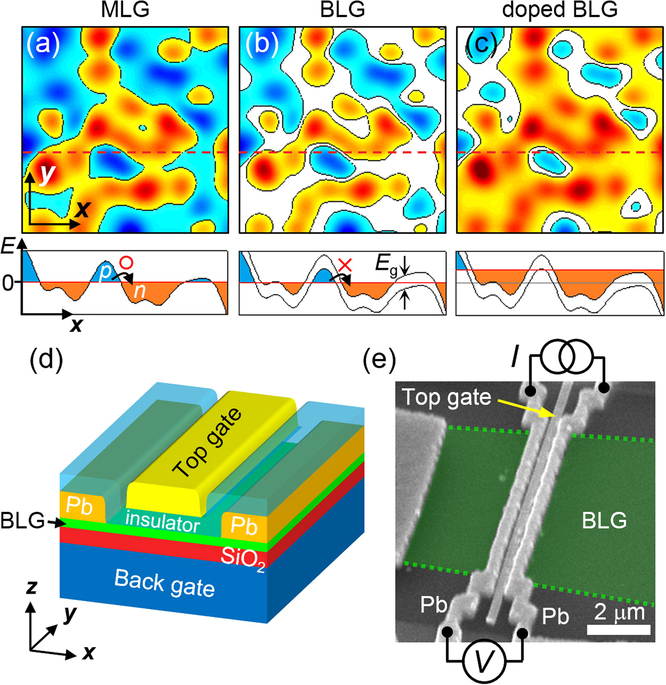
(Upper panels) Spatially distributed charged puddles (a) in monolayer graphene (MLG) or zero-band-gap bilayer graphene (BLG), (b) BLG with a finite band gap Eg in the charge-neutral state, and (c) n-doped finite-band-gap BLG. The red, blue, and white represent n- and p-doped (conducting) and finite-band-gap (insulating) states, respectively. (Lower panels) Cross-sections along the broken red curves in the upper panels, showing the variation in the conduction and valence bands. The solid red curve shows the chemical potential. (d) Schematic diagram showing the configuration of the dual-gated BLG Josephson junction. (e) Scanning electron microscopy image of the device, illustrating the measurement configuration. The green dotted lines show the location of the BLG.
Results
Gate-control of superconducting and insulating states
Figure 1(d) shows a schematic diagram of the configuration of the dual-gated BLG device. A pair of Pb superconducting electrodes was closely attached to a mechanically exfoliated BLG layer, which was sandwiched between the top and bottom gates (see Methods). A scanning electron microscopy image of the device is shown in Fig. 1(e), together with the measurement configuration. The distance (L) between electrodes is 0.46 μm and the width (W) of the BLG is 7.0 μm. The contact resistances between BLG and Pb electrodes were negligibly small compared to the zero-bias junction resistance, R (Supplemental Information, section 1 and Fig. S1). The BLG became superconducting as Andreev-paired carriers formed due to the proximity effect of the superconducting electrodes, along with the consequent Josephson coupling between them33,34,35. The voltages of the bottom gate, Vb, and the top gate, Vt, induced displacement fields Db = εb(Vb − Vb,0)/db and Dt = −εt (Vt − Vt,0)/dt, along the 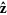 direction, where ε’s are the dielectric constants, d’s are the thicknesses of the dielectric layers, and Vb,0 (Vt,0) is the charge-neutral voltage offset of the bottom (top) gate due to the initial doping. The difference Ddensity = Db − Dt controls the carrier density (or the chemical potential), while the average, Dgap = (Db + Dt)/2, breaks the inversion symmetry of the BLG, opening up a band gap36 (Supplemental Information, section 2 and Fig. S3).
direction, where ε’s are the dielectric constants, d’s are the thicknesses of the dielectric layers, and Vb,0 (Vt,0) is the charge-neutral voltage offset of the bottom (top) gate due to the initial doping. The difference Ddensity = Db − Dt controls the carrier density (or the chemical potential), while the average, Dgap = (Db + Dt)/2, breaks the inversion symmetry of the BLG, opening up a band gap36 (Supplemental Information, section 2 and Fig. S3).
Figure 2(a) shows the square resistance of the junction, Rsq = R × (W/L), as a function of Ddensity and Dgap measured at a base temperature of T = 50 mK. The superconducting and insulating states, marked by black and red symbols, respectively, were determined from the current–voltage (I–V) characteristics at each set of Ddensity and Dgap. The two phases are separated coincidently by the quantum resistance of Cooper pairs, RQ = h/4e2 (green contour line) as observed in other systems. On the weakly insulating side, the system exhibited nonlinear insulating I–V characteristics, as shown in Fig. 2(b), the zero-bias conductance of which is consistent with 2D Mott variable range hopping conduction, G(T) ~ exp[−(T*/T)1/3], where T* is a characteristic temperature (see Methods). On the superconducting side, Rsq eventually vanished, and a dissipationless supercurrent branch emerged, as shown in Fig. 2(c), which resulted from the proximity Josephson coupling (Supplemental Information, section 3 and Fig. S4).
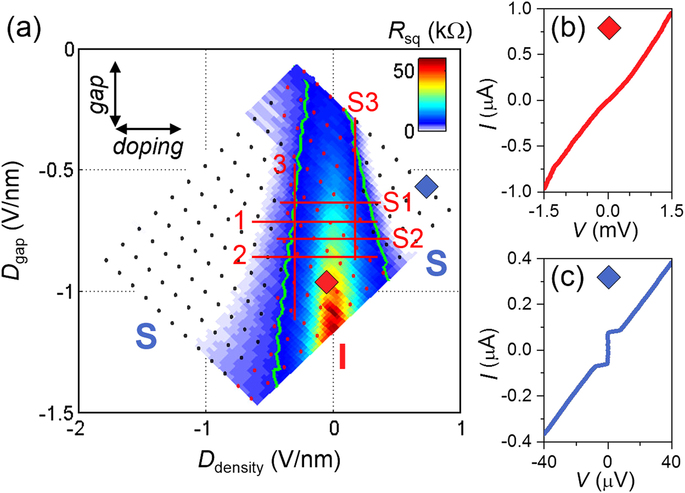
(a) Color-coded square resistance map of the junction as a function of Ddensity and Dgap measured at 50 mK. The diamond symbols indicate representative insulating (red) or superconducting (blue) points of Ddensity and Dgap. The green contours correspond to the quantum resistance of Cooper pairs, RQ = h/4e2, and separate insulating regions from the superconducting regions. The red curves indicate gate sweep traces 1–3 and S1–S3. Current–voltage characteristics taken at the corresponding points denoted in (a) exhibit (b) a nonlinear insulating behavior (the red curve) and (c) zero-resistance superconducting behavior (the blue curve).
Finite-size scaling analysis on the temperature-dependent behavior
The temperature dependence of Rsq at different Ddensity ranging from insulating to superconducting phases is shown in Fig. 3(a). It shows no signs of the re-entrance or kink of the resistance at temperatures down to 50 mK, which was commonly observed in granular films. Below the crossover temperature T0 denoted by the broken line, Rsq saturated, presumably due to Joule heating of charge carriers. The shift of T0 to lower temperatures when the heating was reduced (i.e., when Rsq was smaller) is consistent with the Joule-heating interpretation. In Fig. 3(b), the curves of Rsq vs Ddensity at different temperatures converge on a single point (i.e., Ddensity,c ~ −0.3 Vnm−1) with a corresponding critical square resistance of Rsq,c ~ 1.1RQ, which is close to the universal value predicted by the dirty boson model for a low dissipative system.
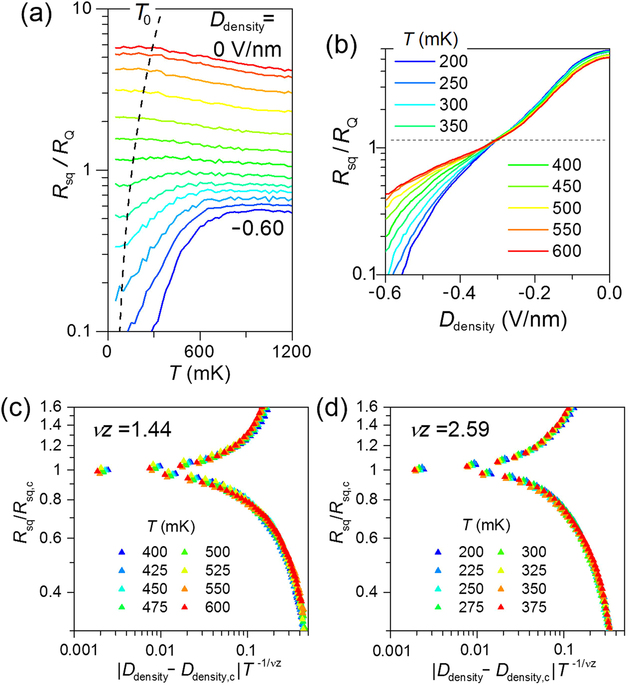
(a) Temperature dependence of the square resistance Rsq with various Ddensity for a fixed Dgap = −0.86 Vnm−1 plotted with a log-linear axis. Ddensity was varied in steps of 0.05 Vnm−1 from 0 Vnm−1 (top) to −0.60 Vnm−1 (bottom). The broken curve indicates the heating-induced crossover temperature T0, below which the electron temperature and Rsq saturated. (b) The data set in (a) plotted as a function of Ddensity at various T. The horizontal broken line indicates the point of convergence. Finite-size scaling analysis of the Ddensity-driven superconductor–insulator transition for sweep 2 in Fig. 2(a). For 400 < T < 600 mK (c), vz = 1.44 gave the best data collapse; however, for temperatures of 200 < T < 375 mK (d), vz = 2.59 resulted in the best data collapse.
The SIT behavior is interpreted as a quantum phase transition (QPT), as confirmed by Rsq vs Ddensity data converging to a single finite-size scaling curve5,6 of the form Rsq = Rsq,c f(xT−1/vz) close to the critical point [Fig. 3(c,d)]. Here, f is a scaling function and x |Ddensity − Ddensity,c| or x |Dgap − Dgap,c| is a tuning parameter. The correlation length exponent ν and the dynamical critical exponent z characterize the universality class of the QPT. The data for 400 < T < 600 mK exhibit the best collapse, with a critical-exponent product of vz = 1.44, which is close to the value vcl = 4/3 for classical percolation in 2D37 [an exponent of z = 1 has been assumed for a system with charged particles1, which also appears to be valid in our study, as discussed separately in the bias-field-tuned critical point]. However, at lower temperatures (i.e., 200 < T < 375 mK), the best collapse was found with vz = 2.59, which is consistent with a quantum percolation transition in 2D with the value vq = 7/3 (semi-classically one expects38 vq = vcl + 1). The best estimates of vq in the literature39 lie in the range 2.3–2.5. We will see below that these values were consistently found in several sweeps with different carrier densities and band gaps. Interestingly, there was a classical-to-quantum crossover at T1 ~ 400 mK, which will be discussed later in a more quantitative manner. Theoretical studies have predicted14,22 such a crossover from quantum to classical percolation due to decoherence at a finite temperature. Observations of similar crossover behavior have been reported22 for quantum Hall insulator transitions. However, no estimation was provided for the associated change in the electron temperature, Tel, introduced by the bias-induced Joule heating.
Estimation of Tel and the classical-to-quantum crossover
Since Joule heating may seriously affect the behavior of the QPT, in particular, close to the lowest measurement temperature, we carried out an in-depth quantitative analysis of Tel. Tel saturated to a temperature T0 as the phonon temperature Tph (i.e., the measurement temperature) approached the base temperature, i.e., Tel = T0 when Tph = 50 mK. The dissipative power P = I2R at Tph = 50 mK was estimated from the saturated resistance R and the root-mean-square (r.m.s.) bias current of I = 1 nA, which exhibited a power-law dependence on T0, as shown in Fig. 4(a), along with the fit to 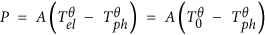 with Tph = 50 mK. The fitting parameters were the electron–phonon coupling exponent θ = 2.8 ± 0.1 and the coefficient A = 77 ± 14 fW∙K−2.8, where T0 was estimated to be T0 = 160 mK at the SIT point of Rsq ~ 1.1RQ (Supplemental Information, section 4 and Fig. S5). The value of θ was consistent with the recently observed value in MLG40 in millikelvin regime.
with Tph = 50 mK. The fitting parameters were the electron–phonon coupling exponent θ = 2.8 ± 0.1 and the coefficient A = 77 ± 14 fW∙K−2.8, where T0 was estimated to be T0 = 160 mK at the SIT point of Rsq ~ 1.1RQ (Supplemental Information, section 4 and Fig. S5). The value of θ was consistent with the recently observed value in MLG40 in millikelvin regime.
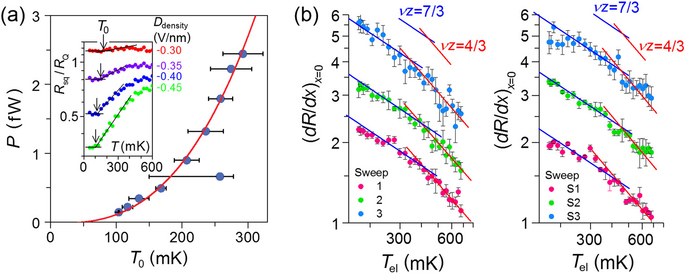
(a) Relationship between the heating-induced crossover temperature T0 and the dissipative Joule-heating power P. The solid curve is a fit to Rsq data close to the transition in a logarithmic scale. The horizontal lines are guides for the levelling-off of Rsq and the arrows indicate T0. (b) Electron temperature (Tel)-dependence of resistance slope (dR/dx)x=0. For clarity, each data set was shifted vertically by an arbitrary offset. The red and blue linear curves indicate the slope expected with classical and quantum percolation, respectively.
With the electron temperature described by 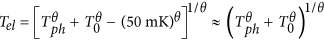 , we now discuss the temperature dependence of the critical exponents in detail. The exponent product vz can be evaluated from the slope of a double logarithmic plot of
, we now discuss the temperature dependence of the critical exponents in detail. The exponent product vz can be evaluated from the slope of a double logarithmic plot of 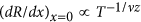 vs T, as shown in Fig. 4(b), for each gate sweep of the Ddensity-tuned (sweep 1, 2, S1, and S2) and Dgap-tuned (sweep 3 and S3) SIT. Note that, in this plot, the heating effect is excluded by replacing the measurement temperature by the electron temperature with T0 = 160 mK. For all gate sweeps, for T > 400 mK, the slope is described well by classical percolation (red line), whereas for T < 400 mK, the slope is consistent with the quantum percolation model (blue line). Successful elimination of the Joule heating effect in this study made it possible to identify a crossover between classical and quantum percolation, with the temperature as a tuning parameter for the decoherence.
vs T, as shown in Fig. 4(b), for each gate sweep of the Ddensity-tuned (sweep 1, 2, S1, and S2) and Dgap-tuned (sweep 3 and S3) SIT. Note that, in this plot, the heating effect is excluded by replacing the measurement temperature by the electron temperature with T0 = 160 mK. For all gate sweeps, for T > 400 mK, the slope is described well by classical percolation (red line), whereas for T < 400 mK, the slope is consistent with the quantum percolation model (blue line). Successful elimination of the Joule heating effect in this study made it possible to identify a crossover between classical and quantum percolation, with the temperature as a tuning parameter for the decoherence.
Finite-size scaling analysis for bias electric field
Similar to the temperature dependence, the bias current (I) dependence of Rsq is also differentiated into two phases as shown in the inset of Fig. 5(a), such that Rsq decreases (increases) with lowering I in the superconducting (insulating) phase. Here, we emphasize that the value of θ satisfies the ‘safety’ criterion6 2/θ > z/(z + 1), where z = 1, for the intrinsic fluctuations being dominant in the Joule-heating effect. This allowed fitting of the critical-exponent product v(z + 1) for both the classical and quantum percolation regions from the scaling behavior as a function of the bias electric field. The finite-size scaling analysis with the electric field (E) in Fig. 5(a,b) provides additional information of v(z + 1), because the E dependence of Rsq has the form Rsq = Rsq,c g[xE−1/v(z+1)] near the critical point6,41. Here, g is another scaling function. Similar to the T-varying scaling in Fig. 3(c,d), E-varying scaling also gives two different values of v(z + 1) depending on the bias current range. For I = 9–15 nA, the best scaling was obtained with v(z + 1) = 2.66, which is close to the value of classical percolation [v(z + 1) = 8/3]. But, for the lower bias current range of I = 3–9 nA the best fit was obtained with v(z + 1) = 4.56, which is close to the value of quantum percolation [v(z + 1) = 14/3].
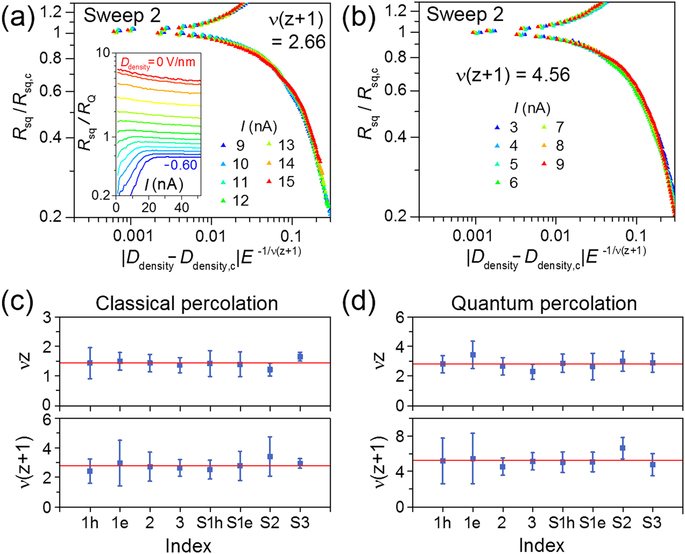
Finite-size scaling analysis of electric field dependences of Ddensity-driven transition for the gate sweep 2, which yields the best collapse with v(z + 1) = 2.66 for I = 9–15 nA in (a) or v(z + 1) = 4.56 for I = 3–9 nA in (b). Inset of (a), bias current dependence of Rsq at different doping levels (Ddensity, from 0 to −0.60 Vnm−1, in steps of 0.05 Vnm−1). Critical-exponent products vz and v(z + 1) evaluated at various critical points for (c) the classical percolation regime and (d) the quantum percolation regime. Red lines represent average values. The characters ‘h’ and ‘e’ in the sweep indices stand for the hole and electron side, respectively.
Products of critical exponents, vz and v(z + 1)
v(z + 1), together with vz from the T-varying scaling, allows an independent determination of the critical exponents41 of v and z. We investigated several critical points for both of Ddensity–driven and Dgap–driven SIT as indicated in Fig. 2(a). For each gate sweep, we performed scaling analysis for both the temperature and electrical field dependences to evaluate the critical-exponent products of vz and v(z + 1), respectively. We summarized all the critical-exponent products in Fig. 5(c,d) for both of the classical and quantum percolation regimes. The corresponding scaling results for the classical percolation regime are shown in supporting information (Supplemental Information, section 5 and Figs S7 and S8). At higher temperatures (T > 400 mK) or for higher electric fields (I > 9 nA), with the averaged values of vz = 1.44 ± 0.13 and v(z + 1) = 2.81 ± 0.31 for all different gate sweeps (sweeps 1–3 and S1–S3), we get v = 1.37 ± 0.34 and z = 1.05 ± 0.27. This result supports the SIT of charged bosons (Cooper pairs) in the classical percolation universality class, which is consistent with the percolative transport nature of carriers through charged puddles in BLG at T = 4.2 K. At lower temperatures (T < 400 mK) or lower electric fields (I < 9 nA), the averaged values of vz = 2.83 ± 0.33 and v(z + 1) = 5.25 ± 0.63 give v = 2.42 ± 0.71 and z = 1.17 ± 0.37, which support the quantum percolation universality class for SIT.
Discussion
It is rather surprising that the BLG layer in the narrow region between the superconducting electrodes show the finite-size scaling behaviour of a 2D SIT, which is usually observed in homogeneous 2D systems. We believe that the temperature range of our transport measurements was sufficiently low as to allow the critical behaviour of the correlation length as a function of temperature. The observed temperature-dependent finite-size scaling was then governed by the temporal scale associated with the system temperature without apparent influence of the spatial scale of our device on the transition characteristics. Apparently, the spatial correlation length remained limited at finite temperatures (i.e., shorter than the spacing between the superconducting electrodes) as to neglect the effects arising from possible inhomogeneity of carrier transport or finite size of our system.
Our BLG devices provide a unique method to investigate the underlying mechanisms of SITs via accurate and reversible control of disorder. Electrical gating changed the average spacing between proximity-induced superconducting puddles to drive the QPT as Andreev-reflected bound pairs at the Fermi level establish long-range coherence via percolative paths to yield the critical power-law behavior of percolation with negligible thermal intervention. At lower temperatures than the range of classical percolation behavior, direct control of the disorder enabled us to estimate the effective electron temperature and consequently to identify the crossover between classical and quantum percolation in a single device. Previously, these two regimes have only been obtained in separate systems belonging to weak and strong disorder regimes21. Our proximity-coupled BLG system demonstrates that it is an exceptionally useful platform to study disorder-induced QPTs.
Methods
Device fabrication
Fabrication of the bilayer-graphene Josephson-junction devices relied on mechanical exfoliation of graphene42 on a highly doped silicon substrate, which was capped with a 300-nm-thick silicon oxide layer to form a bottom gate dielectric (db = 300 nm, εb = 3.9). Bilayer graphene was identified via optical contrast (Supplemental Information, section 6 and Fig. S9). Superconducting electrodes were defined using electron beam lithography and thermal evaporation of Pb0.9In0.1 onto the bilayer graphene. Indium was added to minimize the grain size and the surface roughness35. The junction area was covered with cross-linked poly(methyl methacrylate) (PMMA)43,44, which formed a dielectric layer for the top gate (dt ≈ 43 nm, εt = 4.5). A Ti/Au top-gate electrode stack (where the layers were 5- and 145-nm-thick, respectively) was deposited and accurately aligned to cover most (~90%) of the junction area (Supplemental Information, Fig. S2). This allowed uniform gate control over the entire junction area. The thickness of the top gate dielectric, dt, was determined from the shift of the resistance maximum of Vt by the modulation of Vb. Vb,0 and Vt,0 were determined by comparing the band gap, which was estimated from the temperature dependence in Fig. 6.
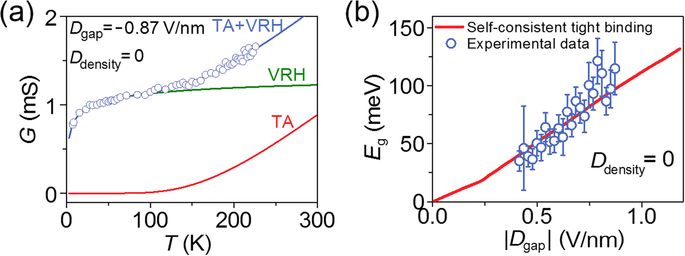
(a) Temperature dependence of conductance G at Dgap = −0.87 V/nm and Ddensity = 0 (charge neutrality point). The data were taken by ac measurements at zero dc bias and are fitted to the parallel conduction model (blue line), which consists of thermally activated conduction (red line) and variable-range-hopping conduction (green line). Best-fit parameters are Eg = 115 ± 23 meV and Th = 1.92 ± 0.59 K. (b) Band gap Eg estimated from the temperature dependence of conductance is plotted as a function of |Dgap|. Red line represents the prediction by self-consistent tight-binding calculation.
Low-noise measurements
The sample was maintained in thermal contact with the mixing chamber of a dilution fridge (Oxford Kelvinox AST) and cooled to a base temperature of 50 mK. Electrical measurement lines were filtered by a combination of two-stage low-pass RC filters (with a cut-off frequency of ~30 kHz) mounted at the mixing chamber and pi-filters (with a cut-off frequency of ~10 MHz), which were at room temperature. We used a conventional lock-in technique with a bias current amplitude 1 nA r.m.s. at a frequency of 13.33 Hz for the temperature-dependent measurements, and a direct-current bias for the bias-field-dependent measurements.
Temperature dependence of conductance at CNP
At the charge neutrality point (Ddensity = 0), the Fermi level is placed in the middle of the bandgap Eg. Then, the conduction occurs with thermally activated carriers, providing the temperature (T) dependence of conductance, GTA(T) = GTA,0 exp(−Eg/2kBT), with Boltzmann constant kB. However, in disordered bilayer graphene, bandgap is filled with the localized states such as conducting electron and hole puddles so that the carriers can hop across these states. Hopping transport is more pronounced at lower temperatures where the thermal activation (TA) is exponentially suppressed. As shown in Fig. 6(a), low-temperature conductance agrees with variable range hopping (VRH) model in two dimensions, GVRH(T) = GVRH,0 exp[−(Th/T)1/3], whereas high-temperature data agree with the TA conduction. The measurement was done at temperatures above ~7 K, with the Pb electrodes in the normal state. The charge neutrality point for the top gate was estimated to be Vt,0 = −6.0 V, where the |Dgap| dependence of resultant fitting parameter Eg agrees with the theoretical prediction of self-consistent tight-binding calculation as shown in Fig. 6(b). Similar TA+VRH transport properties were experimentally investigated in dual-gated bilayer graphene45. We could not directly determine Vt,0 as it was beyond the charge-leakage voltage of the top gate. However, the uncertainty in the determination of Vt,0 gives additional offsets to Dgap only but does not affect the scaling analysis discussed in the text.
Percolation transport in gapped bilayer grapheme
Carrier density inhomogeneity in two-dimensional (2D) GaAs semiconducting systems induces the percolative metal–insulator transition (MIT) in the low carrier density regime31,46. Similarly, graphene which has inhomogeneous charge puddles is also expected to exhibit the percolative MIT if a bandgap is introduced to separate the electron band from the hole band. For example, S. Adam et al.32 fabricated graphene into a nanoribbon structure to open a bandgap in graphene and demonstrated a 2D MIT of the classical percolation universality class. There is also theoretical prediction of percolation behavior for bilayer graphene with a finite bandgap47. In our case, a vertical electric field opened a bandgap in bilayer graphene. We investigated transport properties of bilayer graphene in the presence of the superconducting proximity effect and analyzed them in the frame of percolative superconductor–insulator transition. To support the percolative transport characteristics in gapped bilayer graphene in the absence of superconductivity, we fabricated and performed control experiments with a device consisting of dual-gated bilayer graphene in contact with non-superconducting Ti/Au electrodes. Optical image of the device and the measurement configuration are shown in Fig. 7(a). While injecting current (I = 1 nA r.m.s.) from I+ to I−, voltage drop between V+ and V− was measured as a function of bottom (Vb) and top (Vt) gate voltages at the base temperature of T = 4.2 K. According to the definition of Ddensity and Dgap, a resistance map is plotted as a function of Ddensity and Dgap in Fig. 7(b). Ddensity represents the carrier density (n = 5.52 × 1012 cm−2 × Ddensity∙V−1nm) accumulated by the electrical gates, while Dgap determines opening of bandgap (Eg) in the bilayer graphene. Ddensity dependence of conductance (G) at a fixed Dgap = −0.8 V/nm [along the red line in Fig. 7(b)] is plotted in Fig. 7(c) on log-log scale. The bandgap is estimated to be Eg ~ 90 meV according to the self-consistent tight-binding model30,48. There appears three transport regimes depending on the Ddensity in both electron and hole sides. In a highly doped state (|Ddensity| > 0.5 V/nm), Fermi level exceeds the bandgap (|EF| > 100 meV) so that the system is expected to be in the Boltzmann transport regime49 where 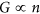 . In the range of 0.1 V/nm < |Ddensity| < 0.5 V/nm, best fits to the critical behavior
. In the range of 0.1 V/nm < |Ddensity| < 0.5 V/nm, best fits to the critical behavior 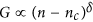 give exponents δh = 1.25 ± 0.02 in the hole side and δe = 1.25 ± 0.05 in the electron side, where nc is the critical carrier density. They are close to the theoretical prediction δ = 4/3 for 2D classical percolation universality class. Near the charge neutrality point, |Ddensity| < 0.1 V/nm, G deviates from the percolation behavior and does not converge to zero but becomes saturated. This is because electron and hole puddles remain conducting even though the average carrier density vanishes at Ddensity = 0. Figure 7(d) shows the same data and corresponding fitting lines of Fig. 7(c) on linear scale. The linear relation between G and n in the Boltzmann transport regime (blue lines) and the crossover between percolation and Boltzmann transport regimes (arrows) are more pronounced.
give exponents δh = 1.25 ± 0.02 in the hole side and δe = 1.25 ± 0.05 in the electron side, where nc is the critical carrier density. They are close to the theoretical prediction δ = 4/3 for 2D classical percolation universality class. Near the charge neutrality point, |Ddensity| < 0.1 V/nm, G deviates from the percolation behavior and does not converge to zero but becomes saturated. This is because electron and hole puddles remain conducting even though the average carrier density vanishes at Ddensity = 0. Figure 7(d) shows the same data and corresponding fitting lines of Fig. 7(c) on linear scale. The linear relation between G and n in the Boltzmann transport regime (blue lines) and the crossover between percolation and Boltzmann transport regimes (arrows) are more pronounced.
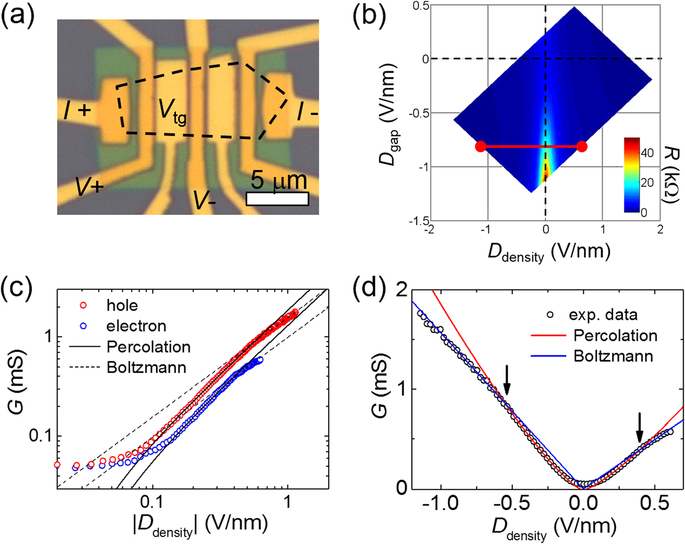
(a) Optical image of the dual-gated bilayer graphene device with measurement configuration. (b) Resistance map as a function of Ddensity and Dgap measured at 4.2 K. (c) Log-log plot of conductance as a function of |Ddensity| in the hole side (red symbols) and electron side (blue symbols). Best fits to the percolation behavior (solid lines) in the range of 0.1 V/nm < |Ddensity| < 0.5 V/nm gives the critical exponent of δh = 1.25 ± 0.02 and the critical carrier density of 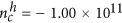 cm−2 in the hole side, and δe = 1.25 ± 0.05 and
cm−2 in the hole side, and δe = 1.25 ± 0.05 and  cm−2 in the electron side. Dotted lines represent the Boltzmann transport behavior for highly doped state (|Ddensity| > 0.5 V/nm). (d) Linear plot of the same data and the fitting lines of (c). Arrows indicate the crossover between Boltzmann and percolation transport regimes.
cm−2 in the electron side. Dotted lines represent the Boltzmann transport behavior for highly doped state (|Ddensity| > 0.5 V/nm). (d) Linear plot of the same data and the fitting lines of (c). Arrows indicate the crossover between Boltzmann and percolation transport regimes.
Additional Information
How to cite this article: Lee, G.-H. et al. Continuous and reversible tuning of the disorder-driven superconductor-insulator transition in bilayer graphene. Sci. Rep. 5, 13466; doi: 10.1038/srep13466 (2015).
References
- 1.
Goldman, A. M. Superconductor-insulator transitions. Int. J. Mod. Phys. B 24, 4081–4101 (2010).
- 2.
Gantmakher, V. F. & Dolgopolov, V. T. Superconductor–insulator quantum phase transition. Phys.-Usp 53, 1 (2010).
- 3.
Haviland, D. B., Liu, Y. & Goldman, A. M. Onset of superconductivity in the two-dimensional limit. Phys. Rev. Lett. 62, 2180–2183 (1989).
- 4.
Paalanen, M. A., Hebard, A. F. & Ruel, R. R. Low-temperature insulating phases of uniformly disordered two-dimensional superconductors. Phys. Rev. Lett. 69, 1604–1607 (1992).
- 5.
Fisher, M. P. A. Quantum phase transitions in disordered two-dimensional superconductors. Phys. Rev. Lett. 65, 923–926 (1990).
- 6.
Sondhi, S. L., Girvin, S. M., Carini, J. P. & Shahar, D. Continuous quantum phase transitions. Rev. Mod. Phys. 69, 315–333 (1997).
- 7.
Sacépé, B. et al. Localization of preformed Cooper pairs in disordered superconductors. Nature Phys. 7, 239–244 (2011).
- 8.
Sherman, D., Kopnov, G., Shahar, D. & Frydman, A. Measurement of a superconducting energy gap in a homogeneously amorphous insulator. Phys. Rev. Lett. 108, 177006 (2012).
- 9.
Steiner, M. A., Boebinger, G. & Kapitulnik, A. Possible field-tuned superconductor-insulator transition in High-Tc superconductors: Implications for pairing at high magnetic fields. Phys. Rev. Lett. 94, 107008 (2005).
- 10.
Stewart Jr., M. D., Yin, A., Xu, J. M. & Valles Jr., J. M. Superconducting pair correlations in an amorphous insulating nanohoneycomb film. Science 318, 1273–1275 (2007).
- 11.
Crane, R. et al. Survival of superconducting correlations across the two-dimensional superconductor-insulator transition: A finite-frequency study. Phys. Rev. B 75, 184530 (2007).
- 12.
Fisher, M. P. A., Weichman, P. B., Grinstein, G. & Fisher, D. S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 40, 546–570 (1989).
- 13.
Shimshoni, E., Auerbach, A. & Kapitulnik, A. Transport through quantum melts. Phys. Rev. Lett. 80, 3352–3355 (1998).
- 14.
Dubi, Y., Meir, Y. & Avishai, Y. Unifying model for several classes of two-dimensional phase transition. Phys. Rev. Lett. 94, 156406 (2005).
- 15.
Ghosal, A., Randeria, M. & Trivedi, N. Inhomogeneous pairing in highly disordered s-wave superconductors. Phys. Rev. B 65, 014501 (2001).
- 16.
Dubi, Y., Meir, Y. & Avishai, Y. Nature of the superconductor-insulator transition in disordered superconductors. Nature 449, 876–880 (2007).
- 17.
Kowal, D. & Ovadyahu, Z. Disorder induced granularity in an amorphous superconductor. Solid State Commun. 90, 783–786 (1994).
- 18.
Spivak, B. & Zhou, F. Mesoscopic effects in disordered superconductors near Hc2. Phys. Rev. Lett. 74, 2800–2803 (1995).
- 19.
Swanson, M., Loh, Y. L., Randeria, M. & Trivedi, N. Dynamical conductivity across the disorder-tuned superconductor-insulator transition. Phys. Rev. X 4, 021007 (2014).
- 20.
Sherman, D. et al. The Higgs mode in disordered superconductors close to a quantum phase transition. Nature Phys. 11, 188–192 (2015).
- 21.
Steiner, M. A., Breznay, N. P. & Kapitulnik, A. Approach to a superconductor-to-Bose-insulator transition in disordered films. Phys. Rev. B 77, 212501 (2008).
- 22.
Kapitulnik, A., Mason, N., Kivelson, S. A. & Chakravarty, S. Effects of dissipation on quantum phase transitions. Phys. Rev. B 63, 125322 (2001).
- 23.
Shahar, D. & Ovadyahu, Z. Superconductivity near the mobility edge. Phys. Rev. B 46, 10917–10922 (1992).
- 24.
Parendo, K. A. et al. Electrostatic tuning of the superconductor-insulator transition in two dimensions. Phys. Rev. Lett. 94, 197004 (2005).
- 25.
Caviglia, A. D. et al. Electric field control of the LaAlO3/SrTiO3 interface ground state. Nature 456, 624–627 (2008).
- 26.
Bollinger, A. T. et al. Superconductor-insulator transition in La2-xSrxCuO4 at the pair quantum resistance. Nature 472, 458–460 (2011).
- 27.
Allain, A., Han, Z. & Bouchiat, V. Electrical control of the superconducting-to-insulating transition in graphene–metal hybrids. Nature Mater. 11, 590–594 (2012).
- 28.
Martin, J. et al. Observation of electron-hole puddles in graphene using a scanning single-electron transistor. Nature Phys. 4, 144–148 (2008).
- 29.
Rutter, G. M. et al. Microscopic polarization in bilayer graphene. Nature Phys. 7, 649–655 (2011).
- 30.
Zhang, Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009).
- 31.
Das Sarma, S. et al. Two-dimensional metal-insulator transition as a percolation transition in a high-mobility electron system. Phys. Rev. Lett. 94, 136401 (2005).
- 32.
Adam, S., Cho, S., Fuhrer, M. S. & Das Sarma, S. Density inhomogeneity driven percolation metal-insulator transition and dimensional crossover in graphene nanoribbons. Phys. Rev. Lett. 101, 046404 (2008).
- 33.
Josephson, B. D. Possible new effects in superconductive tunnelling. Phys. Lett. 1, 251 (1962).
- 34.
Heersche, H. B., Jarillo-Herrero, P., Oostinga, J. B., Vandersypen, L. M. K. & Morpurgo, A. F. Bipolar supercurrent in graphene. Nature 446, 56–59 (2007).
- 35.
Jeong, D. et al. Observation of supercurrent in PbIn-graphene-PbIn Josephson junction. Phys. Rev. B 83, 094503 (2011).
- 36.
McCann, E. Asymmetry gap in the electronic band structure of bilayer graphene. Phys. Rev. B 74, 161403 (2006).
- 37.
den Nijs, M. P. M. A relation between the temperature exponents of the eight-vertex and q-state Potts model. J. Phys. A: Math. Gen. 12, 1857 (1979).
- 38.
Mil’nikov, G. V. & Sokolov, I. M. Semiclassical localization in a magnetic field. JETP Letters 48, 536 (1988).
- 39.
Kramer, B., Ohtsuki, T. & Kettemann, S. Random network models and quantum phase transitions in two dimensions. Physics Reports 417, 211 (2005).
- 40.
Borzenets, I. V. et al. Phonon bottleneck in graphene-based Josephson junctions at millikelvin temperatures. Phys. Rev. Lett. 111, 027001 (2013).
- 41.
Yazdani, A. & Kapitulnik, A. Superconducting-insulating transition in two-dimensional a-MoGe thin films. Phys. Rev. Lett. 74, 3037–3040 (1995).
- 42.
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
- 43.
Huard, B. et al. Transport measurements across a tunable potential barrier in graphene. Phys. Rev. Lett. 98, 236803 (2007).
- 44.
Ki, D.-K. & Lee, H.-J. Quantum Hall resistances of a multiterminal top-gated graphene device. Phys. Rev. B 79, 195327 (2009).
- 45.
Miyazaki, H., Tsukagoshi, K., Kanda, A., Otani, M. & Okada, S. Influence of disorder on conductance in bilayer graphene under perpendicular electric field. Nano Lett. 10, 3888–3892 (2010).
- 46.
Manfra, M. J. et al. Transport and percolation in a low-density high-mobility two-dimensional hole system. Phys. Rev. Lett. 99, 236402 (2007).
- 47.
Rossi, E. & Das Sarma, S. Inhomogenous electronic structure, transport gap, and percolation threshold in disordered bilayer graphene. Phys. Rev. Lett. 107, 155502 (2011).
- 48.
Zhang, L. M. et al. Determination of the electronic structure of bilayer graphene from infrared spectroscopy. Phys. Rev. B 78, 235408 (2008).
- 49.
Hwang, E. H., Adam, S. & Das Sarma, S. Carrier transport in two-dimensional graphene layers. Phys. Rev. Lett. 98, 186806 (2007).
Acknowledgements
This work was supported by the National Research Foundation (NRF) through the SRC Center for Topological Matter (Grant No. 2011-0030046 for HJL), the GFR Center for Advanced Soft Electronics (Grant No. 2012M3A6A5055728 for HJL), the Basic Science Researcher Program (Grant No. 2010-0012134 for MCC), the Max Planck POSTECH/KOREA Research Initiative Program (Grant No. 2011-0031558 for KSP), and the CRI Program at SKKU (Grant No. 2012R1A3A2048816 for KSP), funded by the Ministry of Science, ICT and Future Planning. Work at BGU was supported by a grant from the Israel Science Foundation.
Author information
Author notes
- Gil-Ho Lee
Current address: Department of Physics, Harvard University, Cambridge, MA 02138, USA.
- Dongchan Jeong
Current address: Semiconductor R&D Center, Samsung Electronics Co. LTD., Hwasung 445-701, Republic of Korea.
Affiliations
Department of Physics, Pohang University of Science and Technology, Pohang 790-784, Republic of Korea
- Gil-Ho Lee
- , Dongchan Jeong
- & Hu-Jong Lee
Department of Physics, Sungkyunkwan University, Suwon 440-746, Republic of Korea
- Kee-Su Park
Department of Physics, Ben-Gurion University of the Negev, Beer Sheva 84105, Israel
- Yigal Meir
Department of Applied Physics, Hanyang University, Ansan 426-791, Republic of Korea
- Min-Chul Cha
Authors
Search for Gil-Ho Lee in:
Search for Dongchan Jeong in:
Search for Kee-Su Park in:
Search for Yigal Meir in:
Search for Min-Chul Cha in:
Search for Hu-Jong Lee in:
Contributions
D.J., G.-H.L., and H.-J.L. conceived the idea for the project. G.-H.L. and D.J. fabricated the devices and carried out the experiments. All authors analyzed the data. M.-C.C., Y.M., and K.-S.P. provided theoretical consultation on the scaling analysis. M.-C.C. and H.-J.L. supervised the project. All authors contributed to the discussion and writing the manuscript.
Competing interests
The authors declare no competing financial interests.
Corresponding authors
Correspondence to Min-Chul Cha or Hu-Jong Lee.
Supplementary information
PDF files
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
![]() This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/






