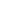Condensation and localization of the partitioning protein ParB on the bacterial chromosome

  1. Ned S. Wingreena,f,1

Author Affiliations

  1. aLewis–Sigler Institute for Integrative Genomics,
  2. bJoseph Henry Laboratories of Physics, and
  3. fDepartment of Molecular Biology, Princeton University, Princeton, NJ 08544;
  4. Departments of cMicrobiology and Immunobiology and
  5. eBiological Chemistry and Molecular Pharmacology, Harvard Medical School, Boston, MA 02115; and
  6. dDepartment of Physics, Ben-Gurion University, Beer Sheva 84105, Israel

  1. Edited by Ken A. Dill, Stony Brook University, Stony Brook, NY, and approved May 1, 2014 (received for review February 10, 2014)

    1. Abstract
    2. Full Text
    3. Authors & Info
    4. Figures
    5. SI
    6. Metrics
    7. Related Content
    8. PDF
    9. PDF + SI

    Significance

    The ParABS system is responsible for chromosome and plasmid segregation in many bacteria. A large, coherent ParB–DNA complex forms the partitioning module at the heart of this segregation machinery. Here we provide a simple theoretical model for interacting proteins on DNA to elucidate the structure of the ParB–DNA complex. We show that that both 3D bridging and 1D spreading interactions between DNA-bound ParB proteins are required to ensure the formation of a coherent protein–DNA complex. This combination of protein–protein interactions implies a surface tension that drives the condensation of ParB proteins on the DNA. The formation of such a condensed protein complex is essential for understanding how a single centromeric parS site can localize ParB on the DNA.

     
    Next Section

    Abstract

    The ParABS system mediates chromosome segregation and plasmid partitioning in many bacteria. As part of the partitioning mechanism, ParB proteins form a nucleoprotein complex at parS sites. The biophysical basis underlying ParB–DNA complex formation and localization remains elusive. Specifically, it is unclear whether ParB spreads in 1D along DNA or assembles into a 3D protein–DNA complex. We show that a combination of 1D spreading bonds and a single 3D bridging bond between ParB proteins constitutes a minimal model for a condensed ParB–DNA complex. This model implies a scaling behavior for ParB-mediated silencing of parS-flanking genes, which we confirm to be satisfied by experimental data from P1 plasmids. Furthermore, this model is consistent with experiments on the effects of DNA roadblocks on ParB localization. Finally, we show experimentally that a single parS site is necessary and sufficient for ParB–DNA complex formation in vivo. Together with our model, this suggests that ParB binding to parS triggers a conformational switch in ParB that overcomes a nucleation barrier. Conceptually, the combination of spreading and bridging bonds in our model provides a surface tension ensuring the condensation of the ParB–DNA complex, with analogies to liquid-like compartments such as nucleoli in eukaryotes.

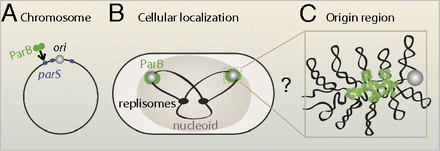
    Chromosomal organization and segregation presents a major challenge in all organisms. Partitioning proteins of the ParABS system play a key role in chromosomal segregation and mediate plasmid partitioning in a variety of bacteria, including Caulobacter crescentus, Bacillus subtilis, and Vibrio cholerae (1, 2). This partitioning module includes a DNA binding protein (ParB) that forms a large nucleoprotein complex at centromere-like parS sites, frequently located near the origin of replication (Fig. 1) (3). These ParB–DNA complexes interact with ParA ATPases, leading to segregation of replicated origins (4⇓⇓⇓–8). Despite the apparent simplicity of this segregation machinery, puzzles remain: What is the nature of interactions among DNA-bound ParB proteins, and how do these determine the organizational and functional properties of the ParB–DNA partitioning complex? A central question is whether ParB spreads along the DNA to form a 1D filamentous protein–DNA complex or assembles into a 3D complex on the DNA. Furthermore, it remains unclear how a small number of parS sites (typically 2–10) leads to robust formation and localization of such a large protein–DNA complex.

    Fig. 1.
    View larger version:
    Fig. 1.

    Cellular localization of ParB. (A) ParB binding sites (parS) are frequently present near the replication origin (ori). (B) In cells, GFP-ParB proteins form fluorescent foci that colocalize with replication origins. The mass of DNA (the nucleoid) is shown schematically as a large oval, including a simplified view of the replicating chromosome (black lines) and the replisomes (black ovals). (C) A hypothetical magnified view of the origin region where ParB forms a large protein–DNA complex.

    Live cell microscopy experiments indicate that ParB-GFP fusion proteins form a large fluorescent focus on the bacterial chromosome (6, 7, 9⇓⇓–12). ParB–DNA complexes do not rely on the presence of ParA or on the particular DNA sequence other than the parS site (12⇓–14). Genome-wide chromatin immunoprecipitation studies (ChIP-chip) in B. subtilis have shown that ParB (Spo0J) binds site-specifically to eight origin-proximal parS sites (13) and also revealed significantly enhanced binding to DNA in the vicinity of each parS site up to distances of 18 kbp. The association of ParB proteins with sites surrounding parS is often referred to as spreading. However, for the sake of clarity, here we refer to this as the formation of ParB–DNA complexes. We reserve the word “spreading” to describe a purely 1D coating of ParB along DNA to form a nucleoprotein filament. The actual structure of the ParB–DNA complexes remains unclear.

    Experiments on P1 plasmids have shown that ParB overexpression leads to silencing of parS-proximal genes (15). However, in many cases gene silencing is only partial and strongly dependent on genomic distance from a parS site, suggesting that the ParB–DNA complex is partially accessible to the transcriptional machinery. Indeed, transcription of genes adjacent to parS sites in B. subtilis is virtually unaffected by Spo0J complex formation at native Spo0J expression levels (13).

    The formation of a ParB–DNA complex at parS suggests the presence of ParB–ParB interactions. In vitro experiments indicate that ParB is largely dimerized in solution owing to its C-terminal dimerization domain. Moreover, the ParB crystal structure from Thermus thermophilus suggests an N-terminal interface that acts as a secondary dimerization domain between DNA-bound ParB proteins (16). In support of this idea, a Spo0J93 mutant that contains a single amino acid substitution near the N terminus (G77S), has wild-type nonspecific and specific DNA binding affinities in vitro but lacks the ability to form ParB–DNA complexes surrounding parS sites on the chromosome in vivo and fails to form discrete fluorescent foci (13). Taken together with the structural data, this suggests that in addition to a C-terminal dimerization domain, ParB (Spo0J) also has an N-terminal interaction domain, which is required to form a ParB–DNA complex.

    Further insight into the nature of ParB–ParB interactions was gleaned from roadblock experiments (15, 17) in which a strong binding site for a transcriptional repressor was inserted near a parS site. In B. subtilis the bound repressor leads to a reduction in ParB binding to DNA adjacent to parS, but only in the direction of the roadblock (17). This was taken as evidence that ParB associates with the DNA by 1D lateral spreading from parS to form a nucleoprotein filament. Alternatively, ParB may form higher-order interactions resulting in a 3D protein–DNA complex.

    To investigate the structure of the ParB partitioning complex, we developed a simple model for interacting proteins on DNA. We found that a combination of 1D spreading bonds and a 3D bridging bond between ParB proteins constitutes the minimal model for condensation of ParB proteins on DNA into a coherent complex. These combined interactions provide an effective surface tension, preventing fragmentation of the complex. In detail, our model predicts that ParB spreads to form multiple, short 1D domains on the DNA, connected in 3D by bridging interactions to assemble into a 3D ParB–DNA condensate (Fig. 1C). More generally, the computational model we developed here offers a simple framework to study how various interactions between DNA-binding proteins determine the structure and localization of protein–DNA complexes.

    Previous SectionNext Section

    Model for Interacting Proteins on DNA

    We developed a minimal model to investigate the spatial organization of interacting proteins on DNA. For simplicity, the DNA is described as a linear, self-avoiding chain on a cubic lattice in 3D; the DNA chain has a bending stiffness κ and N protein binding sites (Supporting Information). The addition of DNA confinement has little effect on our central results (Supporting Information). The DNA is coarse-grained at the scale of a protein-binding site, ℓ0, so that exactly one protein can bind the DNA per site of the cubic lattice.

    Proteins can bind or unbind the DNA and the binding energy may vary along the DNA. Here, we considered a chain with equivalent binding sites, or a chain with just one cognate parS site with a binding energy ΔϵparS relative to all other sites. Importantly, we distinguish two types of protein–protein interactions: (i) 1D spreading interactions with strength JS between proteins along the backbone of the DNA chain and (ii) 3D bridging interactions with strength JB between proteins bound to nonsequential DNA sites that are nearest neighbors in 3D space. We studied the thermodynamic equilibrium behavior of this model via Monte Carlo simulations (Supporting Information).

    Previous SectionNext Section

    Results

    For many bacteria, the faithful partitioning and segregation of plasmids and the chromosome relies on ParB proteins, which form large ParB–DNA complexes localized by a few or in rare cases by one parS site—a 16-bp sequence that specifically binds a ParB dimer (3). We first discuss how various types of protein–protein interactions in our model would affect the structure and stability of the ParB–DNA complex in the absence of a parS site. We then proceed to include a parS site in our model to investigate how this affects the localization of the ParB cluster on the DNA, and finally we consider the role of the parS site in ParB cluster nucleation.

    Combining 1D Spreading with 3D Bridging Interactions Is Necessary for the Formation of a Condensed Protein–DNA Complex.

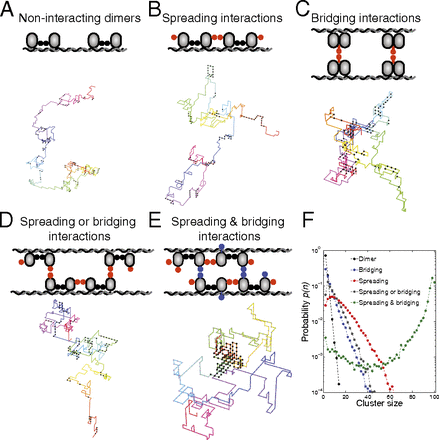
    To serve as a benchmark, we first defined a dimer model, in which DNA-bound proteins interact through their primary dimerization domain (Fig. 2A). An additional dimerization domain on the protein (16, 18) could, in principle, engage in either 1D spreading or 3D bridging interactions leading to two additional models: a spreading model (Fig. 2B) in which each protein in the ParB dimer can form two 1D spreading interactions, one in each direction along the chain, and a bridging model (Fig. 2C), in which each dimer can engage in a single 3D bridging interaction.

    Fig. 2.
    View larger version:
    Fig. 2.

    Simple models for interacting DNA-bound proteins. Schematics include a representative image of a DNA–protein complex from simulations: (A) dimer model, (B) spreading model, (C) bridging model, (D) spreading or bridging model, and (E) spreading and bridging model. In the spreading or bridging model there are two interaction domains per monomer, one of which can be either in spreading or in bridging mode. In the spreading and bridging model there are two 1D spreading bonds along the DNA and one 3D bridging bond. The bond energies are −6kBT except in the spreading or bridging model, for which the bridging bond has an energy of −7kBT. The bending rigidity of the DNA was set to κ=kBTℓ0. The total number of proteins is fixed at m=100 on a DNA chain of length N=500 (i.e., with 500 binding sites). (F) Probability distribution P(n) for a DNA-bound protein to be part of a cluster of size n.

    The dimer, spreading, and bridging models all resulted in multiple protein clusters of varying sizes dispersed over the DNA (with no parS site), as shown in representative images of simulated protein–DNA complexes in Fig. 2 A–C. To quantify the distribution of cluster sizes in a system with a fixed number of proteins, we evaluated the probability P(n) for a randomly chosen protein to be part of a cluster of size n. We defined a cluster to be a 3D, contiguous collection of DNA-bound proteins. For all three models (dimer, spreading, and bridging) we observed a broad distribution peaked at small cluster sizes (Fig. 2F). The enhanced clustering found in the bridging model is consistent with a recent theoretical study showing that bridging can induce an effective entropic attraction between proteins (19). However, with only a single bridging bond per protein, this effective lateral interaction between proteins was found to be weak and the resulting clusters were small, consistent with our results. Changing the interaction strength in both the spreading model and the bridging model can modify the typical cluster size; however, the cluster size distributions remain broad.

    Conceptually, the fragmentation in these models can be traced to the entropy of dispersing the proteins over the DNA, which is favored over the energy of forming a single large cluster. To account for the experimental observation of coherent ParB–DNA foci (6, 7, 9⇓⇓–12), we expanded the model by combining 1D spreading and 3D bridging interactions to avoid entropic fragmentation. In the simplest of such models, the proteins still only have two interaction domains, as in the spreading model, but now one of the interaction domains can either function in spreading or in bridging mode, whereas the other domain can only participate in a 1D spreading bond (Fig. 2D). Importantly, this model failed to prevent fragmentation because the distribution of cluster sizes was broad and qualitatively similar to the previous models (Fig. 2F).

    We next considered a model with one additional ingredient: each ParB protein is able to interact with its two neighbors via 1D spreading interactions along with an additional 3D bridging interaction. Strikingly, in this spreading and bridging model the majority of the proteins cluster together in one coherent focus on the DNA (Fig. 2E). This is reflected as a large, narrow peak centered around the maximal number of proteins in the cluster size distribution (Fig. 2F).

    Importantly, for the spreading and bridging model, unsatisfied dangling ParB bonds at the surface of the cluster generate a surface tension that counters the tendency of entropy to fragment the condensate into multiple small clusters. By contrast, the spreading model cannot support a condensed phase because 1D surface tension always loses to entropy. Moreover, for the bridging model and spreading or bridging model the most stable state consists of small clusters with no surface tension because all bonds can be satisfied. (A variety of other models can be excluded for similar reasons) (Supporting Information). Thus, the combination of both spreading and bridging interactions constitutes the minimal requirement for a condensed phase (i.e., a large, coherent ParB–DNA cluster). These conclusions also hold when we include DNA confinement in our model (Supporting Information).

    A parS Site Can Localize a Condensed ParB Complex.

    DNA-bound ParB proteins localize around parS sites. ParB binds specifically to a parS site, but in vitro experiments suggest that the binding affinity to a parS site is only roughly 10-fold higher than to nonspecific DNA (13). Thus, it is unclear how a few parS sites can localize the majority of ParB proteins.

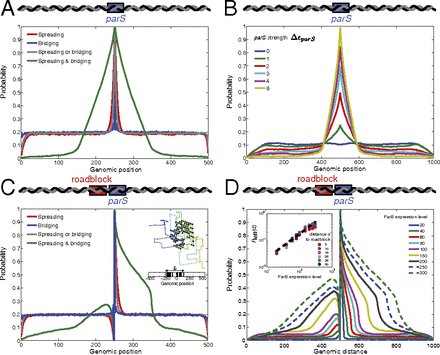
    To investigate the effects of a parS site on the organization of ParB on the DNA, we inserted a site at the center of the DNA in our model with a strong binding energy ΔϵparS=−10kBT relative to the other nonspecific binding sites, where kBT is the thermal energy. Although this parS site binds a protein with a probability close to 1, for the spreading, bridging, and spreading or bridging models the binding probability decays rapidly to a background value ∼0.2, corresponding here to the average coverage of the DNA (Fig. 3A). Thus, in these models the parS site is capable of localizing only one of the small ParB clusters at a time. By contrast, the spreading and bridging model produces a broad binding profile peaked around the parS site, with a binding probability that decays nearly to zero far from the parS site. This approximately triangular binding profile is consistent with the formation of a single, localized ParB–DNA cluster, which can shift as a whole as long as it overlaps with the parS site (Supporting Information). Thus, the ability of one parS site to localize ParB on the DNA in the spreading and bridging model can be traced back to the coalescence of the vast majority of proteins into a large ParB–DNA cluster, ensuring the localization of all these ParB proteins around a sufficiently strong parS site (Fig. 3B and Eq. 2). Finally, we confirmed that the ParB binding profiles remain qualitatively similar when DNA confinement is included (Supporting Information).

    Fig. 3.
    View larger version:
    Fig. 3.

    ParB binding profiles, ParB localization, and the effects of a roadblock. (A) Probability of a bound protein versus genomic position with a central parS site (parameters as in Fig. 2 with ΔϵparS=−10kBT, N=500 binding sites, and m=100 proteins). (B) The probability of a bound ParB versus genomic position for the spreading and bridging model for different ParB–parS binding energies relative to nonspecific sites (N=1,000). (C) A roadblock is inserted immediately to the left of the strong parS site, resulting in an asymmetric spreading profile (N=500). (Inset) ParB–DNA complex with loops from simulations on the spreading and bridging model and the corresponding 1D binding profile on the DNA. (D) Probability of a bound protein versus genomic position for the spreading and bridging model with a roadblock inserted immediately to the left of parS (N=1,000). The total number of ParB proteins on the DNA is varied. (Inset) Scaling of the binding probability, pleft(d), at positions d binding sites to the left of the roadblock as a function of ParB expression level. The dashed line indicates power-law scaling with an exponent of 0.9.

    Roadblocks Strongly Affect the Localization of 3D ParB–DNA Complexes.

    In B. subtilis, the insertion of a strong binding site for a transcriptional repressor in the vicinity of a parS site led to a reduction in ParB–DNA interaction in the direction of the repressor bound site (17). Based on this observation, it was proposed that ParB associates with the DNA by spreading one-dimensionally from a parS site. To investigate the effect of a roadblock on the binding profiles in our models, we inserted a blocked site, to which ParB is not allowed to bind, immediately to the left of the parS site (Fig. 3C). The binding profile of the bridging model is hardly affected by the roadblock, whereas for the spreading model and the spreading or bridging model the binding of ParB is obstructed by the roadblock. Strikingly, the binding profile is also strongly asymmetric for the spreading and bridging model, consistent with the observations from roadblock experiments in B. subtilis (17).

    The small binding probability of ParB to the left of the roadblock for the spreading and bridging model indicates that there are some configurations in which the ParB cluster forms loops that bypass the roadblock. This raises the question why it is thermodynamically more favorable for the complex to stay to the parS side of the roadblock instead of looping around it. To investigate this, we analyzed the loops extruding from the surface of the cluster (Fig. 3C, Inset). Interestingly, we find that the average loop length ⟨ℓ⟩ is independent of cluster size Mc and of the energy of a spreading bond JS (Supporting Information). By contrast, the average number of loops behaves as ⟨Nloops⟩∼exp(−JS/kBT)Mαc, with α=0.9. The formation of a loop requires the breaking of a spreading bond and thus occurs with a probability ∼exp(−JS/kBT). The dependence of ⟨Nloops⟩ on Mc simply reflects the surface area of the cluster, because loops extend from the surface (Supporting Information).

    Intuitively, the greater number of loops in a larger cluster together with the greater number of configurations a larger cluster can adopt on the DNA should render it less sensitive to the presence of a roadblock. Indeed, our simulations show that the binding profiles become more symmetric with increasing ParB expression levels (Fig. 3D), indicating that it becomes more likely to loop around the roadblock for larger clusters. Fig. 3D, Inset demonstrates that the ParB binding probability to the left of the roadblock scales as pleft∼M0.9c over a range of distances d to the left of the roadblock, consistent with theoretical scaling predictions (Supporting Information). Thus, the enhanced probability to bypass a roadblock with increasing ParB levels provides a qualitative prediction that depends on looping and the 3D character of the cluster. Moreover, the scaling of ParB occupancy near a roadblock with ParB expression level allows for a direct experimental determination of the loop exponent α.

    Scaling Behavior for ParB-Induced Gene Silencing.

    Experiments on P1 plasmids indicate that ParB binding to DNA can partially silence genes depending on their distance from parS and on ParB expression levels (15). In contrast, it was found in B. subtilis that transcription was unaffected by the formation of Spo0J nucleoprotein complexes at normal Spo0J expression levels (13). These experiments raise the question of how the presence of a 3D ParB–DNA complex affects the transcriptional machinery.

    To model the effects of a ParB–DNA complex on transcription, we first obtained average parS-proximal binding profiles of ParB on the DNA as a function of ParB expression levels using the spreading and bridging model. Fig. 4A shows how the binding profile broadens with increasing ParB levels, while the shape remains roughly constant. This suggests a rescaling of the genomic distance from parS by the ParB expression level; such a rescaling results in a data collapse, as shown in Fig. 4B (Supporting Information).

    Fig. 4.
    View larger version:
    Fig. 4.

    The effects of ParB cluster formation on gene silencing. (A) Probability of a bound ParB versus genomic position for the spreading and bridging model with a central parS site (JS=−8kBT as solid curves, JS=−6kBT as dashed curves, and other parameters as in Fig. 2). (B) ParB binding profiles from A with genomic position rescaled by ParB expression. (C) Average exposure of the DNA versus ParB expression levels at various distances from the parS site (JS=−6kBT). (D) DNA exposure versus ParB expression rescaled by the distance to the parS site with JS=−8kBT (circles), JS=−6kBT (triangles), and JS=−4kBT (diamonds). (E) Experimental gene-silencing data obtained in P1 plasmids from ref. 15 together with collapse (F). Remaining activities of chloramphenicol acetyltransferase (CAT) and β-galactosidase (β-Gal) were determined.

    What does this scaling property of the ParB profile mean for the effects of ParB–DNA complex formation on gene silencing? We used the exposure of the DNA (defined as 1 − ParB binding probability) as a simple proxy for the remaining activity of a gene at a particular distance from the parS site, defined relative to the activity of a gene without ParB. To compare with the experiments of Rodionov et al. (15) using plasmid P1, we plotted the DNA exposure as a function of ParB expression levels for varying genomic distances from the parS site, as shown in Fig. 4C. These simulation results can also be collapsed for a fixed value of the spreading bond strength JS by plotting the DNA exposure as a function of ParB expression level/parS distance (Fig. 4D). To test the scaling prediction of our model, we plot the experimental data of Rodionov et al. (15) (Fig. 4E) in the same way. Strikingly, this results in a similar data collapse over a broad range of ParB expression levels (Fig. 4F). Thus, our spreading and bridging model predicts that there are protein concentration regimes in which there will be no gene silencing and other regimes in which the ParB–DNA complex will significantly attenuate transcription, and both regimes are captured by a single scaling function.

    The Role of the parS Site in ParB–DNA Complex Formation and Localization.

    Interestingly, ParB does not condense into foci in cells lacking parS sites (Fig. 5C and Supporting Information and ref. 12). This is perplexing in light of in vitro experiments showing that the binding affinity of ParB to a parS site is only 10-fold higher than to nonspecific DNA (13).

    Fig. 5.
    View larger version:
    Fig. 5.

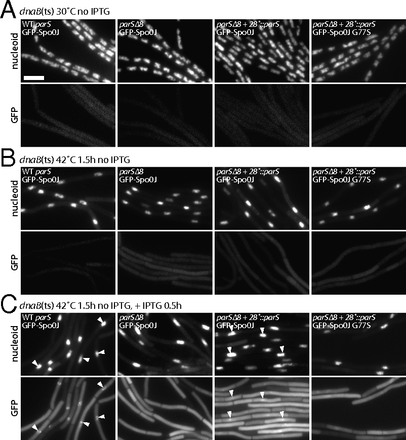
    A single parS site is necessary and sufficient to generate a GFP-Spo0J focus. (A) Representative images of B. subtilis cells harboring a dnaB(ts) allele with all eight wild-type parS sites (BWX2454, WT parS, first panel); none of the eight endogenous parS sites (BWX2456, parSΔ8, second panel); parSΔ8 with an ectopic parS site inserted at 28° (amyE) (BWX2458 and BWX2789, parSΔ8+28°::parS, third and fourth panels) grown at 30 °C (A) and after growth at 42 °C for 1.5 h (B) to block new rounds of initiation of replication generating a single chromosome (Supporting Information). Expression of GFP-Spo0J (first to third panels) or GFP-Spo0J (G77S) (fourth panel) was then induced by the addition of IPTG (0.5 mM final concentration) for 0.5 h at 42 °C (C) (see Supporting Information for induction control). GFP-Spo0J did not form foci in the strain lacking parS sites (parSΔ8, second panel) and formed a single focus per nucleoid in the parSΔ8+28°::parS strain (third panel). GFP-Spo0J (G77S) did not form foci in theparSΔ8+28°::parS strain (fourth panel). Based on comparison with Spo0J (G77S) (C, fourth panel) that binds parS but is unable to spread to neighboring sites (13), the foci observed in the parSΔ8+28°::parS strain (C, third panel) reflect GFP-Spo0J nucleoprotein complexes. Gray scale of DAPI-stained nucleoids (upper panels) and GFP (lower panels) is shown. GFP-Spo0J foci (white carets) are highlighted in the DAPI and GFP panels. (Scale bar, 4 μm.)

    We can rule out a purely thermodynamic basis for the mechanism by which a parS site robustly produces a ParB–DNA complex. We found that, in general, the formation of a ParB–DNA complex in the spreading and bridging model does not rely on the presence of a parS site (Fig. 2 E and F). The affinity of a parS site contributes at most several kBT (13) to the free energy of the ParB–DNA complex, which is much smaller than stabilizing or destabilizing contributions that will arise from natural fluctuations in ParB levels. Thus, a purely thermodynamic stabilization of the ParB–DNA complex by a parS site would require an unrealistic degree of fine-tuning of cellular parameters.

    Nucleation kinetics offers an alternative, robust mechanism to account for the role of a parS site in cluster formation. Even if cells always operate under conditions thermodynamically favoring the ParB–DNA condensed state, substantial nucleation barriers can kinetically impede the formation of a ParB–DNA condensate. We can envision two scenarios for how ParB/parS functions to overcome a nucleation barrier. In the first, two (or more) ParB dimers bound to nearby parS sites form a nucleation center from which ParB–DNA complexes grow (Supporting Information). The relative ParB binding affinity to a parS site is far too low for this kind of nucleation to occur reliably at a single parS site but not elsewhere on the DNA, as explained further below. In the second scenario, nucleation occurs at a single parS site because some characteristic of ParB when bound to a parS site dramatically enhances the rate of complex nucleation.

    To distinguish between these two models, we sought to determine whether a ParB–DNA complex (or a GFP-ParB focus) could be generated in cells that contain only one parS site. Indeed, previous cytological experiments indicate that B. subtilis cells that harbor a single parS site form GFP-Spo0J fluorescent foci (12). However, the cells analyzed in these experiments were actively growing and therefore undergoing DNA replication. Accordingly, before their segregation, the replicated sister parS sites could together serve as a nucleation center for ParB–DNA complexes. To more rigorously test whether a single parS site was sufficient to generate a ParB–DNA complex, we constructed a set of strains harboring a temperature-sensitive replication initiation mutant (dnaBts) (20) to block new rounds of DNA replication. These strains also contained an isopropyl β-d-1-thiogalactopyranoside (IPTG)-inducible GFP-Spo0J fusion as the sole source of Spo0J (ParB), allowing conditional expression of GFP-Spo0J after replication had ceased. We compared a strain that had the full complement of endogenous parS sites (WT parS), a strain lacking all eight parS sites (parSΔ8), and one in which a single ectopic parS site was inserted at a nonessential locus (parSΔ8+28°::parS). Finally, we also constructed a matched control strain harboring a single parS site, containing an IPTG-inducible GFP-spo0J mutant (G77S) that binds parS in vivo but does not form a ParB–DNA complex (14). When grown at the permissive temperature (30 °C) in the absence of IPTG, all four strains contained DAPI-stained chromosomes (called nucleoids) that resembled the chromosomes observed in the Spo0J null mutant (Fig. 5A). Importantly, GFP-Spo0J fluorescence was virtually undetectable (Fig. 5A). After 1.5 h of growth at the restrictive temperature (42 °C), virtually all cells in the four strains contained a single replicated chromosome (Fig. 5B and Supporting Information). At this time, IPTG was added to induce expression of GFP-Spo0J. Thirty minutes later, GFP-Spo0J localization was monitored. As expected, the cells harboring the endogenous origin-proximal parS sites had a single fluorescent focus (or cluster of foci) that colocalized with the nucleoid (Fig. 5C). Moreover, the cells lacking parS sites had no detectable GFP-Spo0J foci. By contrast, virtually all cells with a single parS site had a faint GFP-Spo0J focus that colocalized with the nucleoid. These foci correspond to Spo0J-DNA condensates and not simply a Spo0J dimer bound to the parS site because no foci were detected in the GFP-Spo0J (G77S) mutant that binds parS but does not form a nucleoprotein complex (Fig. 5C). Immunoblot analysis indicates that the GFP-Spo0J fusions were expressed at similar levels in the different strains and the cytoplasmic fluorescence was not due to proteolytic release of GFP (Supporting Information). Taken together, these data indicate that a single parS site per cell is capable of forming a Spo0J-DNA complex, whereas no complex forms in the absence of a parS site. We therefore favor a model in which a Spo0J dimer bound to a parS site is able to nucleate a Spo0J–DNA complex much more rapidly than a Spo0J dimer bound elsewhere.

    Importantly, the requisite parS-induced reduction of the nucleation free-energy barrier, ΔFparS, would have to be dramatic because nucleation of ParB–DNA clusters does not occur at any of the nonspecific DNA binding sites on the chromosome over multiple cell lifetimes under normal conditions. Thus, parS-specific nucleation would have to be considerably more than N≈1.3×105 times faster than nucleation at a nonspecific site assuming a 30-bp footprint for ParB (17); this implies exp(−ΔFparS/kBT)>N, or equivalently,

    ΔFparS<−kBTln(N).
    [1]

    However, the relative affinity of specific binding of ParB (Spo0J) to parS binding was found to be only 10-fold higher than nonspecific binding (13), corresponding to ΔϵparS≈−2.3kBT. Thus, the specificity of a parS site is far too low for simple nucleation to occur reliably at a single parS site, but not elsewhere on the chromosome. A related conundrum is that the measured specificity of parS sites is theoretically insufficient to localize the ParB–DNA complex; the free-energy contribution from the parS site is required to be larger than the entropy gained by delocalizing the cluster over the DNA,

    ΔFparS<kBTln(2McN−2Mc).
    [2]Here, we assumed that this cluster extends over ∼ Mc out of a total of N binding sites on the DNA. In a typical B. subtilis cell, Mc≈1,000 (21) and N≈1.3×105, thus requiring ΔFparS<−4.2kBT, also lower than the experimental value of ΔϵparS≈−2.3kBT (13). Thus, the measured weak specificity of ParB binding to a parS site cannot account for the localization of the ParB–DNA complex, nor can it explain the parS-specific nucleation of ParB–DNA clusters. This analysis provides additional support for the idea that binding of ParB to a parS site facilitates nucleation of a ParB–DNA complex, beyond simply enhancing the local ParB density on the DNA.

    Previous SectionNext Section

    Discussion

    In summary, we have identified a minimal model for interacting ParB proteins on DNA that produces large, coherent ParB–DNA complexes, as observed in live cells (6, 7, 9⇓⇓–12). This model offers a conceptual framework in which a combination of 1D spreading and 3D bridging protein–protein interactions thermodynamically stabilizes a ParB–DNA condensate. Put simply, we find that both spreading and bridging interactions are required to provide a surface tension that prevents fragmentation of condensed protein–DNA complexes. Indeed, we speculate that the ParB–DNA complex may organize like a liquid-like (non–membrane-bound) compartment analogous to, e.g., the nucleolus in eukaryotes (22, 23).

    The spreading and bridging model accounts for multiple experimental observations, including ParB reorganization by DNA roadblocks and ParB-induced gene silencing. What aspects of the model are essential to explain these experiments? The roadblock experiments indicate the presence of strong spreading bonds between ParB proteins (17), and the formation and localization of a coherent ParB–DNA complex (6, 7, 9⇓⇓–12) requires an additional bridging bond between proteins. Crystallographic studies of ParB proteins indicate that there are at least two interaction domains: one at the C terminus that likely promotes dimerization and one at the N terminus (16). An N-terminal Spo0J mutant (G77S) binds parS in vivo but fails to form nucleoprotein complexes. Accordingly, this domain is likely to function in either 1D spreading or 3D bridging. Our model predicts that each ParB monomer has three interaction domains, and thus can form two spreading interactions along the DNA as well as one bridging interaction with another DNA-bound ParB protein, resulting in the formation of clusters consisting of multiple 1D spreading domains of ParB connected in 3D by bridging interactions to form a coherent ParB–DNA complex. These structural predictions could be tested by single-molecule pulling experiments on condensed ParB–DNA complexes. Recent single-molecule experiments using flow-stretched DNA provide evidence for bridging interactions between ParB proteins in vitro, consistent with our model (24). These experiments also show that ParB is capable of condensing DNA with rates up to ∼1μm/s. Interestingly, polymer dynamics theory suggests that the kinetics of DNA condensation in vivo may be slow but could be enhanced in the presence of type-II topoisomerases (25).

    We showed experimentally that a single parS site is both necessary and sufficient for nucleation of a ParB–DNA complex. These experiments together with calculations based on our model led us to conclude that binding of ParB to a parS site effectively lowers the nucleation barrier, leading reliably to complex nucleation at parS sites but not at nonspecific sites. Curiously, we find that the requisite parS-induced reduction of the nucleation barrier has to be much larger than the energy difference inferred from the measured binding affinity of ParB to parS versus nonspecific sites. What mechanism could give rise to a dramatically reduced nucleation barrier at a parS site? It has been speculated based on structural data that the ability of DNA-bound ParB proteins to interact may require a conformational change (16). This proposed conformational transition may involve breaking the primary C-terminal dimerization bond. Thus, there may be two binding modes: ParB could bind to the DNA as closed inert dimers as in our dimer model, or as open dimers as in our spreading and bridging model (Fig. 2 A and E). Building on this idea, we conjecture that the transition to the open configuration is favored at a parS site, whereas the closed configuration is favored at nonspecific sites. An estimate based on this scenario is that the nucleation barrier at a parS site, relative to nonspecific sites, is lowered by E0≈11.5kBT, using the dissociation constant Kd≈10μM for ParB dimerization in solution (16). Combining this with the contribution from binding ParB specifically to a parS site gives ΔFparS≈−13.8kBT, which meets both the nucleation and localization requirements (Eqs. 1 and 2). Thus, this parS-specific two-state nucleation model solves the puzzle of how a single parS site can be necessary and sufficient for the production and localization of a ParB–DNA complex. Importantly, equilibrium behavior of this two-state model is equivalent to our one-state spreading and bridging model (Supporting Information).

    The biophysical properties of the ParB–DNA complex implied by our model may have important implications for the segregation and organization of the chromosome. The surface tension of the ParB–DNA complex in the spreading and bridging model indicates that it is thermodynamically most favorable to form a single ParB–DNA complex that recruits all ori-proximal parS sites. Our model highlights a puzzling aspect of the observed splitting of the parB–DNA complex during segregation (6, 7, 9⇓⇓–12), which would be disfavored by the surface tension of the ParB–DNA complex. This suggests that the splitting of the ParB–DNA complex may rely on active processes, in the case of B. subtilis, likely mediated by the ParA ATPase and the action of structural maintenance of chromosomes condensin complexes (26, 27).

    Our model may also help provide insights into the organization of DNA by nucleoid-associated proteins (NAPs). The model offers a simple framework to study how the specific types of protein-protein interactions in NAPs determine the structure and function of protein–DNA complexes.

    Previous SectionNext Section

    Materials and Methods

    Bacteria Strains and Growth.

    All B. subtilis strains were derived from the prototrophic strain PY79. Cells were grown in defined rich casein hydrolysate medium (28) at indicated temperatures. Strains, plasmids, oligonucleotide primers, and our data analysis are described in Supporting Information.

    Previous SectionNext Section

    Acknowledgments

    We thank B. Bratton, Z. Gitai, B. Machta, and M. Tikhonov for insightful discussions. This work was supported in part by a Lewis–Sigler fellowship (to C.P.B.), National Science Foundation Grant PHY-0957573 (to N.S.W.), National Institutes of Health Grants GM086466 and GM073831 (to D.Z.R.), National Science Foundation CAREER Award MCB-1148818 (to J.J.L.), the Human Frontier Science Program (X.W.), and the hospitality of the Aspen Center for Physics (National Science Foundation Grant PHYS-1066293).

    Previous SectionNext Section

    Footnotes

    • Author contributions: C.P.B., J.J.L., D.Z.R., and N.S.W. designed research; C.P.B. and X.W. performed research; C.P.B., X.W., Y.M., J.J.L., D.Z.R., and N.S.W. analyzed data; and C.P.B., D.Z.R., and N.S.W. wrote the paper.

    • The authors declare no conflict of interest.

    • This article is a PNAS Direct Submission.

    • This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1402529111/-/DCSupplemental.

    Previous Section
     

    References

    1. ↵
      1. Toro E,
      2. Shapiro L
      (2010) Bacterial chromosome organization and segregation. Cold Spring Harb Perspect Biol 2(2):a000349.
      Abstract/FREE Full Text
    2. ↵
      1. Surtees JA,
      2. Funnell BE
      (2003) Plasmid and chromosome traffic control: How ParA and ParB drive partition. Curr Top Dev Biol 56:145–180.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    3. ↵
      1. Livny J,
      2. Yamaichi Y,
      3. Waldor MK
      (2007) Distribution of centromere-like parS sites in bacteria: Insights from comparative genomics. J Bacteriol 189(23):8693–8703.
      Abstract/FREE Full Text
    4. ↵
      1. Banigan EJ,
      2. Gelbart MA,
      3. Gitai Z,
      4. Wingreen NS,
      5. Liu AJ
      (2011) Filament depolymerization can explain chromosome pulling during bacterial mitosis. PLOS Comput Biol 7(9):e1002145.
      CrossRefMedlineGoogle Scholar
    5. ↵
      1. Gerdes K,
      2. Howard M,
      3. Szardenings F
      (2010) Pushing and pulling in prokaryotic DNA segregation. Cell 141(6):927–942.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    6. ↵
      1. Shebelut CW,
      2. Guberman JM,
      3. van Teeffelen S,
      4. Yakhnina AA,
      5. Gitai Z
      (2010) Caulobacter chromosome segregation is an ordered multistep process. Proc Natl Acad Sci USA 107(32):14194–14198.
      Abstract/FREE Full Text
    7. ↵
      1. Toro E,
      2. Hong SH,
      3. McAdams HH,
      4. Shapiro L
      (2008) Caulobacter requires a dedicated mechanism to initiate chromosome segregation. Proc Natl Acad Sci USA 105(40):15435–15440.
      Abstract/FREE Full Text
    8. ↵
      1. Vecchiarelli AG,
      2. Hwang LC,
      3. Mizuuchi K
      (2013) Cell-free study of F plasmid partition provides evidence for cargo transport by a diffusion-ratchet mechanism. Proc Natl Acad Sci USA 110(15):E1390–E1397.
      Abstract/FREE Full Text
    9. ↵
      1. Kusiak M,
      2. Gapczynska A,
      3. Plochocka D,
      4. Thomas CM,
      5. Jagura-Burdzy G
      (2011) Binding and spreading of ParB on DNA determine its biological function in Pseudomonas aeruginosa. J Bacteriol 193(13):3342–3355.
      Abstract/FREE Full Text
    10. ↵
      1. Lin DC,
      2. Levin PA,
      3. Grossman AD
      (1997) Bipolar localization of a chromosome partition protein in Bacillus subtilis. Proc Natl Acad Sci USA 94(9):4721–4726.
      Abstract/FREE Full Text
    11. ↵
      1. Mohl DA,
      2. Gober JW
      (1997) Cell cycle-dependent polar localization of chromosome partitioning proteins in Caulobacter crescentus. Cell 88(5):675–684.
      MedlineWeb of ScienceGoogle Scholar
    12. ↵
      1. Sullivan NL,
      2. Marquis KA,
      3. Rudner DZ
      (2009) Recruitment of SMC by ParB-parS organizes the origin region and promotes efficient chromosome segregation. Cell 137(4):697–707.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    13. ↵
      1. Breier AM,
      2. Grossman AD
      (2007) Whole-genome analysis of the chromosome partitioning and sporulation protein Spo0J (ParB) reveals spreading and origin-distal sites on the Bacillus subtilis chromosome. Mol Microbiol 64(3):703–718.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    14. ↵
      1. Lee PS,
      2. Lin DC,
      3. Moriya S,
      4. Grossman AD
      (2003) Effects of the chromosome partitioning protein Spo0J (ParB) on oriC positioning and replication initiation in Bacillus subtilis. J Bacteriol 185(4):1326–1337.
      Abstract/FREE Full Text
    15. ↵
      1. Rodionov O,
      2. Lobocka M,
      3. Yarmolinsky M
      (1999) Silencing of genes flanking the P1 plasmid centromere. Science 283(5401):546–549.
      Abstract/FREE Full Text
    16. ↵
      1. Leonard TA,
      2. Butler PJ,
      3. Löwe J
      (2004) Structural analysis of the chromosome segregation protein Spo0J from Thermus thermophilus. Mol Microbiol 53(2):419–432.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    17. ↵
      1. Murray H,
      2. Ferreira H,
      3. Errington J
      (2006) The bacterial chromosome segregation protein Spo0J spreads along DNA from parS nucleation sites. Mol Microbiol 61(5):1352–1361.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    18. ↵
      1. Surtees JA,
      2. Funnell BE
      (1999) P1 ParB domain structure includes two independent multimerization domains. J Bacteriol 181(19):5898–5908.
      Abstract/FREE Full Text
    19. ↵
      1. Brackley CA,
      2. Taylor S,
      3. Papantonis A,
      4. Cook PR,
      5. Marenduzzo D
      (2013) Nonspecific bridging-induced attraction drives clustering of DNA-binding proteins and genome organization. Proc Natl Acad Sci USA 110(38):E3605–E3611.
      Abstract/FREE Full Text
    20. ↵
      1. Glaser P,
      2. et al.
      (1997) Dynamic, mitotic-like behavior of a bacterial protein required for accurate chromosome partitioning. Genes Dev 11(9):1160–1168.
      Abstract/FREE Full Text
    21. ↵
      1. Rokop ME,
      2. Auchtung JM,
      3. Grossman AD
      (2004) Control of DNA replication initiation by recruitment of an essential initiation protein to the membrane of Bacillus subtilis. Mol Microbiol 52(6):1757–1767.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    22. ↵
      1. Hyman AA,
      2. Simons K
      (2012) Cell biology. Beyond oil and water—phase transitions in cells. Science 337(6098):1047–1049.
      Abstract/FREE Full Text
    23. ↵
      1. Weber SC,
      2. Brangwynne CP
      (2012) Getting RNA and protein in phase. Cell 149(6):1188–1191.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    24. ↵
      1. Graham TGW,
      2. et al.
      (2014) Parb spreading requires dna bridging. Genes and Development, in press.
      Google Scholar
    25. ↵
      1. Sikorav JL,
      2. Pelta J,
      3. Livolant F
      (1994) A liquid crystalline phase in spermidine-condensed DNA. Biophys J 67(4):1387–1392.
      CrossRefMedlineWeb of ScienceGoogle Scholar
    26. ↵
      1. Wang X,
      2. Montero Llopis P,
      3. Rudner DZ
      (2013) Organization and segregation of bacterial chromosomes. Nat Rev Genet 14(3):191–203.
      CrossRefMedlineGoogle Scholar
    27. ↵
      1. Wang X,
      2. Tang OW,
      3. Riley EP,
      4. Rudner DZ
      (2014) The SMC condensin complex is required for origin segregation in Bacillus subtilis. Curr Biol 24(3):287–292.
      CrossRefMedlineGoogle Scholar
    28. ↵
      1. Youngman PJ,
      2. Perkins JB,
      3. Losick R
      (1983) Genetic transposition and insertional mutagenesis in Bacillus subtilis with Streptococcus faecalis transposon Tn917. Proc Natl Acad Sci USA 80(8):2305–2309.
      Abstract/FREE Full Text

    HighWire Press-hosted articles citing this article
    Text-to-speech function is limited to 100 characters