Research Activity, Highlights
Semi-linear response for the heating rate of cold atoms in vibrating traps
We are working on the absorption rate of particles that are confined by
vibrating walls in a box. This subject was of interest in past
linear response theory (LRT) studies of nuclear friction, where it
leads to the damping of the wall motion. More recently, it has become
of interest in the context of cold atoms physics. One wonders what
happens if the "billiard" is
fully chaotic but with nearly integrable shape. We show
that the analysis that is relevant to the typical experimental
conditions (collaboration with Nir Davidson at Weizmann Institute,
Rehovot, Israel) should go beyond LRT, and should involve a "resistor network" picture of
transitions in energy space, somewhat similar to a percolation
problem. Each unperturbed energy level of a particle in a vibrating
trap, or of an electron in a mesoscopic ring, is regarded as a node (n) of the network; The transition
rates (w_{mn}) between the
nodes are regarded as the elements of a random matrix that describes
the network. This theory was called the semi-linear response theory (SLRT).
We show that if the perturbation matrix is "sparse'' or "textured''
(notably if its elements (x) have log-normal or log-box rather than
Gaussian distribution), as determined by the geometry of the system, the results are different compared
with LRT. Consequently, we predicted that the rate of
energy absorption would be suppressed by orders of magnitude and
introduced an improved sparse random matrix model which leads to a
generalized variable range hopping picture. Our analytical estimates
were supported by a numerical calculation.
[1] A. Stotland, D. Cohen and N. Davidson, Europhysics Letters
86, 10004 (2009) [arXiv]
[pdf].
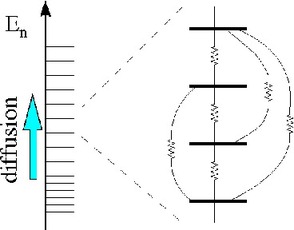
In the first row there are different possible types of perturbation
matrices: "banded Gaussian", "textured", "textured and sparse".
In the second row the "resistor network" in energy space is presented,
and next to it there is a histogram of sparse matrix elements.
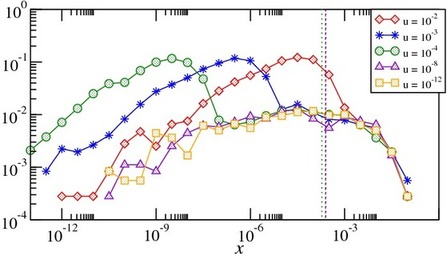
The mesoscopic conductance of disordered rings
We have also applied the semi-linear response theory to calculate the mesoscopic conductance of small
metallic rings driven by Aharonov-Bohm flux (in
collaboration with the group of Tsampikos Kottos at Wesleyan
University, Middletown, Connecticut, USA). Consider a
multichannel closed ring with disorder (W).
In the semi-classical treatment its conductance (G) is given by the Drude formula.
Our theory challenges this result both in the limit of strong disorder
(eigenstates are not quantum-ergodic in real space) and in the limit of
weak disorder (eigenstates are not quantum-ergodic in momentum space).
- Our theory implies that the correct quantum result for the
conductance of a ballistic ring is neither Landauer-like nor Drude.
- In the strong disorder limit our theory provides a firm unified
framework from which the "hopping" phenomenology of Mott can be derived.
Also in this problem the texture
and the sparsity of the perturbation matrix dictate the value of
the conductance, and we studied its dependence on the disorder
strength, ranging from the ballistic to the Anderson localization
regime. In particular we have obtained practical approximations for the
conductance of mesoscopic rings.
[1] A.
Stotland, R. Budoyo, T.
Peer, T. Kottos and D. Cohen, J. Phys. A 41, 262001 (FTC) (2008) [arXiv]
[pdf],
Editor's choice of 2007-2008
[2] A. Stotland, T. Kottos and D. Cohen, (2009)
[arXiv]
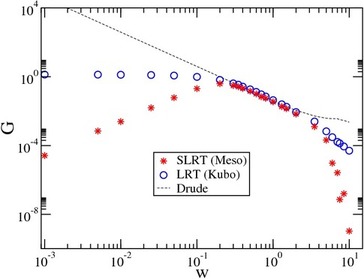
The SLRT, LRT and Drude conductance vs. the disorder strength.
Diffractive energy spreading and its
semiclassical
limit
We consider driven systems where the driving induces jumps in energy space:
- particles pulsed by a step potential;
- particles
in a box with a moving
wall;
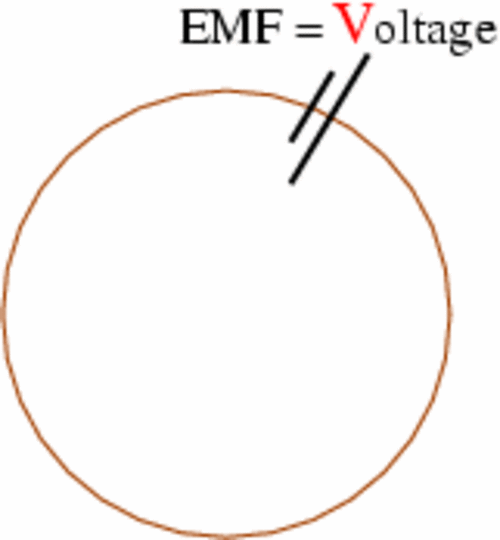
- particles in a ring driven by an
electro-motive-force.
In all these
cases the route towards quantum-classical correspondence is highly
non-trivial.
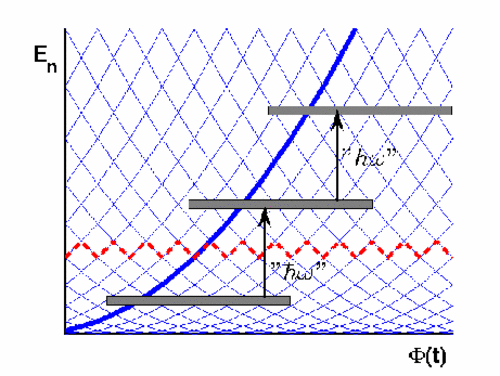
Some insight is gained by observing that the
dynamics in energy space, where n is
the level index, is essentially the same as that of
Bloch electrons in a
tight binding model, where n is the
site index. The mean level spacing is
like a constant electric field and the driving induces long range
hopping 1/(n-m).
[1] A. Stotland and D. Cohen, J. Phys. A 39, 10703 (2006) [arXiv] [pdf]
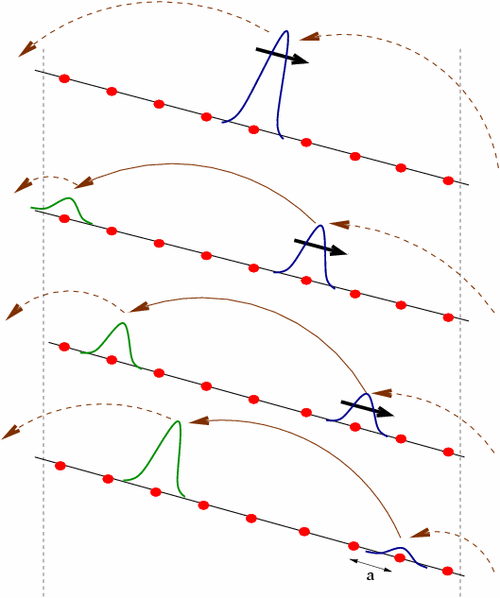
In the above illustration the EMF is concentrated at one point along
the ring. Whenever a particle crosses the EMF region its kinetic
energy is boosted. The energy jump is eV.
From quantum mechanical point of view this constitutes a
non-perturbative effect. It is neither "adiabatic"
nor "diabatic", but rather a "semiclassical" transition. In the analagous tight
binding model the semicalssical dynamics is regarded as uni-directional Bloch oscillations.
The information
entropy of quantum mechanical states
It is well known that a Shannon based definition of
information entropy leads
in the classical case to the Boltzmann entropy. It is tempting to
regard the
Von Neumann entropy as the corresponding quantum mechanical definition.
But the
latter is problematic from quantum information point of view.
Consequently
- we
introduce a new definition of entropy that reflects
the inherent uncertainty of
quantum mechanical states.
- we derive for it an
explicit expression, and discuss
some of its general properties.
- we distinguish between the minimum
uncertainty
entropy of pure states, and the excess
statistical entropy of mixtures.
[1] A. Stotland, A.A. Pomeransky, E. Bachmat, D. Cohen, Europhysics Letters
67, 700 (2004) [arXiv]
[pdf]