Diffusion and localization in sparse networks

Real symmetric matrices

Our interest is in real symmetric conservative matrices. \[ \mathbf{W} = \left(\matrix{ -\gamma_{1} & w_{12} & w_{13} & \cdots & \cdots \cr w_{12} & -\gamma_2 & w_{23} & \cr w_{13} & w_{23} & -\gamma_3 & \cr \vdots & & & \ddots\cr \vdots & & & & \ddots}\right) \] The "conservative" means that each row's sum is zero, or: \[\gamma_n \ \ \equiv \ \ \sum_{m\neq n} w_{mn} \]

Motivation

Such matrices appear in rate equations: \[ \frac{d}{dt}{\mathbf p} \ \ = \ \ \mathbf{W}\cdot\mathbf{p} \] in Newtons II law for systems of masses and springs, which are used as heat transport models: \[ \frac{d^2}{dt^2}{\mathbf q} \ \ = \ \ -\mathbf{K}\cdot\mathbf{q} \] and in Schrödinger's equation \[ \frac{d}{dt}{\mathbf \psi} \ \ = \ \ -i {\mathcal{H}}\cdot\mathbf{\psi} \]

Sparsity

We focus on sparse/glassy networks, where by sparse we mean that a small number of elements is larger by orders of magnitude than the rest.

As two examples we use:

  1. Response of driven weakly chaotic systems

  2. Mott random site model

    In this model, the sites are randomly distributed in space, and the rates depend on the distance between sites: \[ w_{nm} \ \ =\ \ w_0 \cdot \exp\left(-\frac{\left|r_n-r_m\right|}{\xi} - \epsilon_{nm}\right)\] Where \(\xi\) and \(w_0\) are system parameters (defining the time and space units), and \(\epsilon\) a bond specific parameter. In the degenerate version, \(\epsilon=0\) for all the bonds, while in the non-degenerate version \(\epsilon_{nm} = \textrm{uniform}[0,\infty]\).

    The dimensionless parameter defining sparsity in this model is \[ s \ \ =\ \ \frac{\xi}{r_0} \] where \(r_0\) is the typical distance between sites.

    3. gamma distribution
    A visual example: the distribution of \(\gamma\) (arbitrary units), for a \(2d\) system with 300 sites and \(\varepsilon=0\). We see that even though the distribution is translational invariant, some sites are better connected to others.

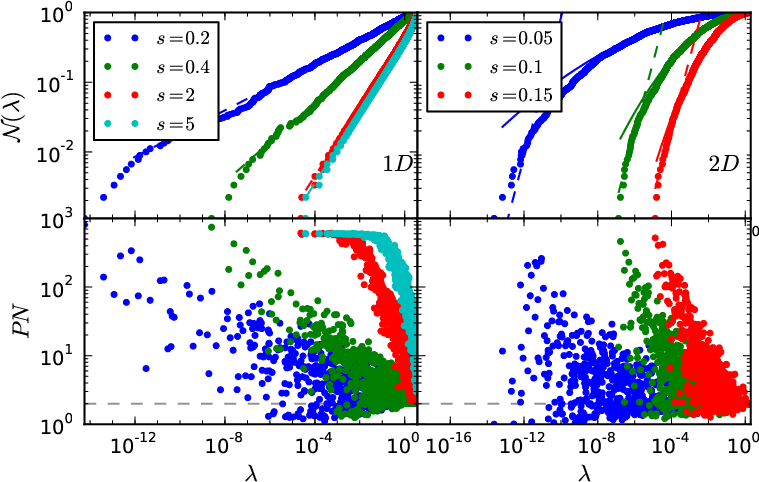
    Determining the diffusion coefficient \(D\)

    The long term behavior of the system is characterized by a diffusion coefficient \(D\). It is defined by the long term spreading: \[ S(t)\quad = \quad \left\langle r^2(t)\right\rangle \quad \sim \quad D t\] And it is also related to the long time survival probability: \[ \mathcal{P}(t)\quad \sim \quad \frac{1}{(Dt)^{1/2}} \] And to the low eigenvalue distribution (by Laplace transform): \[ \mathcal{N}(\lambda) \quad \sim \quad \left[ \frac{\lambda}{D}\right]^{d/2} \]

    Spectral counting function \(\mathcal{N}(\lambda)\) and PN, for \(1d\) and \(2d\). For \(1d\) the dashed lines were found analytically. For \(2d\) they are based on Resistor-Network calculation.

    On the left: exact \(1d\) analytical result, for spreading and \(D\). On the right: \(2d\) numerics, with the linear and ERH estimates.

    Effective range hopping

    For a dense system, (large \(\xi\) compared to typical site distance), the diffusion coefficient can be estimated by a linear equation (linear in the rates): \[ D_{\textrm{linear}} = \frac{1}{2d}\sum_r w(r) r^2 \] We present the ERH procedure to estimate \(D\), based on resistor network analysis, with a smooth cross-over between the dense and sparse regimes.

    Results for the degenerate model

    \[ D \quad =\quad \textrm{EXP}_{d+2}\left(\frac{1}{s_\textrm{eff}}\right) \mbox{e}^{-1/s_\textrm{eff}} D_{\textrm{linear}} \\ s_\textrm{eff}\quad=\quad \left(\frac{d}{\Omega_d} n_c\right)^{-1/d}\frac{\xi}{r_0} \\ \textrm{EXP}_{l}(x) \quad = \quad \sum_{k=0}^l \frac{1}{k!}x^k\]

    Results for the non-degenerate "Mott" model

    In this case, \(s_\textrm{eff}\) depends explicitly on the temperature, i.e.: \[s_{\textrm{eff}}\quad=\quad \left(\frac{d}{\Omega_d} n_c \left(\frac{T}{\Delta_\xi}\right)\right)^{-1/(d+1)} \] Where \(\Delta_\xi\) is the mean level spacing. Apart from that, the only change in \(D\) is the polynomial order: \[ D \quad =\quad \textrm{EXP}_{\color{red}{d+3}}\left(\frac{1}{s_{\textrm{eff}}}\right) \mbox{e}^{-1/s_{\textrm{eff}}} D_{linear} \] In the limit \(s\ll 1\), we get the familiar VRH estimate that has been presented long ago by Nevill Francis Mott. \[ D \sim \left(\frac{1}{T}\right)^{2/(d+1)} \exp\left[-\left(\frac{T_0}{T}\right)^{1/(d+1)}\right]\]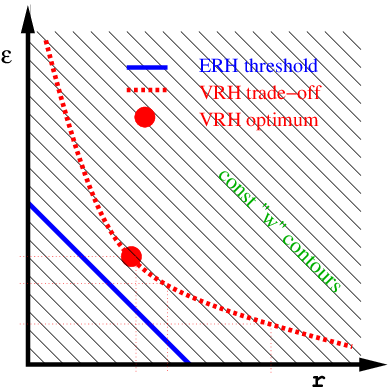
    Comparing the VRH trade-off with the ERH threshold

    Diffusion in sparse networks: linear to semi-linear crossover [arXiv] [pdf],
    Y. de Leeuw, D. Cohen, Phys. Rev. E 86, 051120 (2012).