תרגילים במכניקה קוונטית
חזרה על אלגברה לינארית
exercise
(1020) מטריצות פאולי
מטריצות פאולי, לרבות מטריצת היחידה, מוגדרות להיות:
\( \sigma_0=1=\left( \array{ 1 & 0 \\ 0 & 1 } \right) ,\, \sigma_1= \left( \array{ 0 & 1 \\ 1 & 0 } \right) ,\, \sigma_2= \left( \array{ 0 & -\imath \\ \imath & 0 } \right) ,\, \sigma_3= \left( \array{ 1 & 0 \\ 0 & -1 } \right) \)
מטריצות פאולי ומטריצת היחידה מהווים בסיס
שלם למטריצות 2x2
בהנתן אופרטור
\( A \)
מגדירים את היצוג שלו באמצעות הפיתוח
\( A=\sum_i a_i\sigma_i \)
בפרט אפשר להגדיר מטריצות שדומות למטריצות פאולי בצורה הבאה
\( \sigma_n = \vec{n} \cdot \vec{\sigma}, \,\,\, \vec{n}=\text{unit vector}, \,\,\, \vec{\sigma}=(\sigma_1,\sigma_2,\sigma_3) \)
בהמשך השאלה נתיחס למטריצות הבאות:
\( H_1 = \left( \matrix{1 & 2 \cr 2 & 1} \right), \,\,\,\, H_2 = \left( \matrix{6 & 3 \cr 3 & -2} \right) \)
-
רישמו את מטריצות פאולי בכתיב דיראק.
-
ודאו שאתם מכירים את טבלת הכפל ואת הקומוטטורים של מטריצות פאולי.
-
הוכיחו שמתקיים
\(\sigma_n^2 = 1 \).
מכאן שהערכים העצמיים של מטריצות אלו, שדומות למטריצות פאולי, הם
\( \pm 1\)
-
רישמו את המטריצות
\(H_1, H_2 \)
באמצעות מטריצות פאולי.
-
חשבו את המכפלה
\( H_1 H_2 \)
ואת הקומוטטור
\( [H_1,H_2] \)
תוך הסתמכות על טבלת הכפל של מטריצות פאולי.
-
מה הערכים העצמיים של המטריצות? נא לא לפתור משוואות ריבועיות כדי לענות על שאלה זו!
-
הראו שאפשר לחשב את
\( Tr(H_1 H_2) \)
על ידי כפל סקלרי של וקטורי ההצגה
\( a_i \)
של המטריצות.
exercise
(1025) אופרטורי היטל כבסיס להצגה
אופרטורי ההיטל
\( P^{n}, \, Q^{nm}, \, R^{nm} \)
על
\( N^2 \)
המצבים
\( |n\rangle,\,\,\, \frac{1}{\sqrt{2}} (|n\rangle+|m\rangle),\,\,\, \frac{1}{\sqrt{2}}(|n\rangle+i|m\rangle) \)
מהווים בסיס שלם להצגת האופרטורים מעל מרחב הילברט
\( N \)
מימדי.
רשום את האופרטור המיוצג על ידי המטריצה שלהלן באמצעות אופרטורי היטל
כאלה.
\( A=\left( \array{ 3 & 0 & 0 &0 \\ 0 & 7 & 2 & i \\ 0 & 2 &5 & 0 \\ 0 &-i &0 &9 } \right) \)
הדרכה: בשלב ראשון הגדר מטריצות פאולי מוכללות
\( X^{nm} = 2Q^{nm}-P^{n}-P^{m},\,\, Y^{nm} = 2R^{nm}-P^{n}-P^{m} \)
.
ורשום את האופרטור A באמצעות
\( P^{n}, \, X^{nm}, \, Y^{nm} \)
(לא נדרשת כאן שום עבודה אלגברית).
בשלב שני בטא את התוצאה באמצעות אופרטורי ההיטל.
exercise
(1060) שינוי בסיס של וקטור
נתון מרחב הילברט הנפרש על ידי הבסיס האורתונורמלי
\( \{|1 \rangle, \ |2 \rangle \} \)
מגדירים בסיס אורתונורמלי חדש
\( \{|u \rangle, \ |v \rangle \} \)
נתון כי
\( |u \rangle =a|1 \rangle +b|2 \rangle \)
-
מה התנאי לכך שהמצב
\( |u \rangle \)
יהיה מנורמל?
-
הגדר את המצב
\( |v\rangle \)
כך שהבסיס החדש יהיה אורתונורמלי.
-
יצג בבסיס הסטנדרטי את אופרטורי ההיטל על מצבי הבסיס החדש.
-
ציין האם יש חופש בתשובות לסעיפים (2) ו-(3).
-
רשום את מטריצת המעבר מהבסיס הישן לבסיס החדש.
-
בטא את
\( |\psi \rangle =3 |1 \rangle +7|2 \rangle \)
בבסיס החדש.
exercise
(1140) לכסון אופרטורים
נניח כי בבסיס מסוים האופרטורים
\( A \)
ו
\( B \)
מיוצגים ע"י המטריצות
\( A= \left( \array{ a & 0 & 0 \\ 0 & -a & 0 \\ 0 & 0 & -a } \right) ,\, B= \left( \array{ b & 0 & 0 \\ 0 & 0 & \imath b \\ 0 & -\imath b & 0 } \right) \)
-
האם ל
\( B \)
יש ע"ע מנוונים?
-
הראה כי
\( A \)
ו
\( B \)
חילופיים.
-
מצא בסיס חדש בו
\( A \)
ו
\( B \)
אלכסוניים בו-זמנית.
מערכות בעלות מימד הילברט סופי
exercise
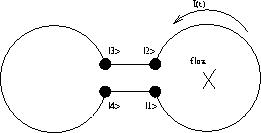
(1322) המילטוניאן של מערכת 4 אתרים / שני קיוביטים
נתונה מערכת 4 אתרים המסודרים בצורת "ריבוע". ניתן לחשוב על המערכת כעל "טבעת". המיקום של חלקיק מוגדר על ידי אופרטור
מיקום \( \hat{x} \) שיכול לקבל ערך שלם \( x \) (מודולו 4), אופרטור ההזזה \( \hat{D} \) מזיז את החלקיק צעד אחד נגד כיוון השעון. המצבים העצמיים
שלו הם מצבי התנע. אופרטור התנע מוגדר כמקובל \( \hat{p} |k\rangle = k |k\rangle \). בהמשך השאלה נתון שהמערכת סימטרית תחת הזזות. אמפליטודת הקפיצה בין אתרים סמוכים היא \( c \), ואין שדה מגנטי.
- רשמו את אופרטור המיקום \( \hat{x} \), המוגדר על פי \( \hat{x} |x\rangle = x |x\rangle \).
- רשמו את אופרטור ההזה \( \hat{D} \) בבסיס הנקבע על ידי \( \hat{x} \).
- מצאו את הערכים והוקטורים העצמאים של אופרטור ההזה.
- רשמו את ההצגה של אופרטור ההזה על ידי אופרטור התנע \( \hat{p} \).
- רשמו את ההמילטוניאן של המערכת.
- הביעו את ההמילטוניאן בעזרת אופרטור ההזזה.
- רשמו ביטוי של ההמילטוניאן בעזרת אופרטור התנע ומצאו את האנרגיות העצמאיות.
קיימת פרשנות אופציונלית של המערכת. אפשר להגיד שמדובר במערכת של שני קיוביטים. מצבי הבסיס הם \( |q_1,q_2\rangle \) באשר \( q=0,1 \) הם המצבים של קיוביט.
- הסבירו מדוע מדובר בהמילטוניאנים זהים מבחינה מתמטית.
- סמנו את המצבים העצמיים של כל קיוביט בסימון \( | \pm \rangle \)
- רשמו את האנרגיות של המצבים העצמיים \( |+,+\rangle, |+,-\rangle, |-,+\rangle, |-,-\rangle \)
- הסבירו מדוע התוצאה של 10 קונסיסטנטית עם התוצאה של סעיף 7.
exercise
(1323) המילטוניאן של מערכת 4 אתרים
נתונה מערכת 4 אתרים המסודרים בצורת "ריבוע". אנרגית הקשר של כל האתרים זהה. כל האתרים מחוברים זה לזה (גם אלכסונית).
אמפליטודת הקפיצה בין כל שני אתרים היא \( c \). אין שדה מגנטי.
- רשמו את מטריצת ההמילטוניאן שמתארת את המערכת.
- הראו שההמילטוניאן מתלכסן בבסיס התנע. מה הן האנרגיות העצמיות?
- רישמו את ההמילטוניאן באמצעות אופרטור ההזזה \( D \).
- רישמו את ההמילטוניאן באמצעות אופרטור התנע \( p \).
- ודאו שהתוצאה של סעיף 4 תואמת את מה שמצאתם בסעיף 2.
- מה האנרגיות העצמיות אם אמפליטודות הקפיצה האלכסוניות הן \( c_{\perp} \ne c \).
טיפ: בסעיף 2 קל מאוד לראות איך ההמילטוניאן פועל על מצבי התנע אם מוסיפים \( c \) באלכסון. כך שלא נדרשת עבודה שחורה כדי לקבל את האנרגיות העצמיות.
exercise
(1328) מעבר דרך צומת בשריג חד-מימדי
2014A
בבעיה זו נדרש למצוא את מקדם המעבר
\( g=|t|^2 \)
של חלקיק בעל תנע
\( k \)
דרך צומת בשריג חד-מימדי (ראה ציור).
נתונים: קבוע השריג
\( a \)
, תדירות הקפיצה
\( c_0 \)
בין אתרים שכנים, ותדירות הקפיצה
\( c_J \)
בין האתרים
\( n=\pm1 \)
.
בסעיף (1) הנח שמדובר בשריג בלתי מופרע, שבו במקום צומת יש אתר נוסף
\( n=0 \)
(1) רשום את ההמילטוניאן הבלתי מופרע
\( H_0 \)
, ואת אופרטור המהירות
\( v \)
כפונקציה של אופרטור התנע
\( p \)
(2) רשום את המטריצה
\( H_{n,m} \)
שמיצגת את ההמילטוניאן המופרע.
מספיק לרשום תת-מטריצה 4x4 עבור
\( n,m=-2,-1,1,2 \)
(3) רשום מערכת של שתי משוואות עבור אמפליטות המעבר וההחזרה
\( (r,t) \)
של הצומת (ראה הדרכה)
(4) רשום ביטוי עבור מקדם המעבר
\( g \)
כפונקציה של
\( k \)
.
(5) עבור
\( c_J \)
גדול מאוד או קטן מאוד
\( g \propto |v_k|^2 \)
. רשום את מקדמי הפרופורציה.
הדרכה:
על מנת לפתור את בעית הפיזור הנח גל פוגע מצד שמאל
\( \psi_n=e^{ikx_n}+re^{-ikx_n} \)
וגל עובר בצד ימין של הצומת
\( \psi_n= te^{ikx_n} \)
באשר נקודות השריג הן
\( x_n= na \)
.
שתי המשוואות שמתקבלות מתוך
\( H\psi=E_k\psi \)
נראות עם הרבה איברים במבט ראשון -
אך למעשה רוב האיברים מתחסלים, ומתקבלת מערכת משוואות מאוד פשוטה.
נא להשתמש בנתוני השאלה בלבד!
exercise
(1330) תנודות בלוך לאורך שרשרת
2020B
תדירות הקפיצה של חלקיק בין אתרים סמוכים של שרשרת היא
\(-c/2\)
.
בנוסף יוצרים שדה חשמלי
\( f\)
. מטען
החלקיק הוא
\(e=1\).
לצורך נירמולים אפשר להניח שהשרשרת מורכבת מ-
\(L\)
אתרים.
מגדירים אופרטור מקום
\(x\)
עם ערכים
עצמיים
\(n=\text{integer}\)
ואופרטור תנע
\(p\)
עם ערכים עצמיים
\(k\)
(1) רשום את ההמילטוניאן כפונקציה של האופרטורים
\(x,p\)
ופתור את משוואות התנועה הקלאסיות עבור
\((x(t),
p(t))\)
בהנתן תנאי התחלה.
(2) רשום את משוואת המצבים העצמיים בהצגת התנע(!).
מצא את המצבים העצמיים בהצגה זו:
\(\Psi_k =
\langle k | \nu=\text{integer} \rangle \)
מתוך תנאי השפה (בתנע) קבע מה הן האנרגיות העצמיות
\(E_{\nu}\)
(3) רשום מה המצבים העצמיים בהצגת המקום:
\(
\psi_n = \langle n | \nu \rangle\)
(4) הכינו את החלקיק באתר
\(x=n_0\)
מה היא ההסתברות
\(P_t(n|n_0)\)
למצוא אותו באתר
\(n\)
לאחר פרק זמן
\(t\)
.
[סעיף זה דורש מעט אלגברה].
זהויות שימושיות:
\(J_{\ell}(\gamma) = \int_{-\pi}^{\pi}
\frac{d\varphi}{2\pi} e^{i[\ell\varphi - \gamma
\sin(\varphi)]}\)
\(\sin(\varphi)-\sin(\varphi_0) =
2\sin\left(\frac{\varphi-\varphi_0}{2} \right)
\cos\left(\frac{\varphi+\varphi_0}{2} \right)\)
exercise
(1343) תנודות בריבוע עם 9 אתרים
2020A
גרסא דיסקרטית של בור פוטנציאל חד מימדי היא שרשרת שלושה אתרים.
מצבי הבסיס הם
\( |x=-1,0,1\rangle\)
גרסא דיסקרטית של בור פוטנציאל דו מימדי הוא ריבוע עם 9 אתרים.
מצבי הבסיס הם
\( |x=-1,0,1,\,\,\,
y=-1,0,1\rangle\)
תדירות הקפיצה בין אתרים סמוכים (בכיוון האנכי או האופקי) היא
\(c\)
.
להלן מכינים חלקיק באתר המרכזי של הבור.
(1) רשום את המצבים העצמיים והאנרגיות העצמיות של חלקיק בשרשרת של 3
אתרים.
(2) מצא את ההסתברות
\(P_{1D}(t) \)
למצוא את החלקיק באתר המרכזי לאחר פרק זמן
\(t\)
(3) רשום את המצב התחילי של החלקיק בריבוע כסופר-פוזיציה של שלושה
מצבים עצמיים.
רשום בצורת טבלה את האמפליטודות
\(\Psi_{x,y}\)
של כל אחד משלושת המצבים העצמיים,
וציין מה היא האנרגיה העצמית של כל מצב.
(4) מצא את ההסתברות
\(P_{2D}(t) \)
למצוא
את החלקיק באתר המרכזי לאחר פרק זמן
\(t\)
(5) יוצרים פוטנציאל
\(u\)
באתר
המרכזי של הריבוע. חשב את התיקון לשלושת האנרגיות העצמיות עד סדר
שני.
exercise
(1344) תנודות בין אתר לטבעת
2011B
נתונה טבעת באורך
\( L=1 \)
שכוללת N אתרים בעלי פוטנציאל זהה (אפס). אמפליטודת הקפיצה של חלקיק ליחידת זמן בין אתרים שכנים היא
\( c \)
. מוסיפים אתר במרכז הטבעת. אנרגית הקשר של החלקיק באתר המרכזי היא
\( \varepsilon_0 \)
. אמפליטודת הקפיצה ליחידת זמן מהאתר המרכזי לכל אחד מאתרי הטבעת היא
\( c_0 \)
. את המערכת שמים בשדה מגנטי כך שהשטף הכולל דרך הטבעת הוא
\( \Phi \)
. מטען החלקיק הוא e. מהאנליזה להלן נובע שהחלקיק יבצע תנודות בין האתר לבין הטבעת. זו הכללה של תנודה במערכת שני אתרים.
-
רשום את ההמילטוניאן
\( H_{ring}(p) \)
של חלקיק בטבעת שתוארה לעיל (ללא האתר המרכזי).
-
רשום את האנרגיות העצמיות
\( E_n \)
של החלקיק בטבעת (ללא האתר המרכזי).
-
חשב את הצימודים
\( \langle E_n | H | \varepsilon_0 \rangle \)
של האתר המרכזי למצבי הטבעת.
-
מה תדירות התנודה
\( \Omega \)
של החלקיק.
-
עבור שטף מגנטי נתון - מה צריכה להיות אנרגית הקשר
\( \varepsilon_0 \)
על מנת לקבל תנודות מלאות.
-
לתדירות
\( \Omega(\Phi) \)
יש תלות מחזורית בשטף המגנטי. מה המחזור על בסיס אהרונוב-בוהם?
הבע את התשובות תוך שימוש בנתוני השאלה בלבד.
exercise
(1346) חלקיק בבאר כפולה שמצומדת לרמה גבוהה
2013B
חלקיק מצוי בבאר כפולה סימטרית. ניתן להתייחס למערכת כמורכבת מאתר "1"
ומאתר "2".
אנרגית הקשר לכל אחד משני האתרים היא אפס. אמפליטות הקפיצה ביניהם
היא
\( c_0 \)
.
בנוסף קים אתר "0" שהאנרגיה הפוטנציאלית שלו
\( \varepsilon_0 \)
היא הרבה יותר גבוהה, ומתקיים
\( c_0 \ll \varepsilon_0 \)
.
אמפליטודת הצימוד של אתר "0" למצבי הבאר הן
\( c_1, \ c_2 \)
.
המשימה העיקרית להלן היא למצוא את ההמילטוניאן האפקטיבי 2x2 שמתאר את
החלקיק בבאר הכפולה.
לשם כך עליך לעבור לבסיס חדש שכולל מצב "D" ומצב "C" שהם סופרפוזיציות
של מצב "1" ומצב "2".
בסעיפים 1-3 הנח שאפליטות הקפיצה בין האתרים היא
\( c_0=0 \)
.
-
הגדר מצב אפל "D" שהצימוד שלו לאתר "0" הוא אפס.
-
הגדר מצב "C" אורתוגונלי למצב "D", ומצא את הצימוד
\( \langle 0 | H |C \rangle \)
-
על ידי שימוש בתורת הפרעות סדר שני קבע את האנרגיות של המצבים C,
D שהגדרת
-
רשום המילטוניאן אפקטיבי 2x2 שמתאר את החלקיק בבסיס הסטנדרטי.
-
עבור איזה ערך של
\( c_0 \)
המצב העצמי של החלקיק יהיה ממוקם באתר
יחיד.
טיפים:
-
התשובה בסעיף 3 מגדירה המילטוניאן אפקטיבי
\( H=\left( \matrix{E_D & 0 \cr 0 & E_C} \right) \)
-
התשובה בסעיף 4 היא אותו המילטוניאן בבסיס הסטנדרטי, מיוצג על
ידי מטריצה לא אלכסונית.
-
בסעיף 4 יש להוסיף להמילטוניאן את הצימוד
\( c_0 \)
-
התשובה בסעיף 5 מתקבלת מתוך התבוננות על ההמילטוניאן שמצאת בסעיף
4
exercise
(1352) זרם דרך בונד שמחבר שני אתרים
2022A
מכינים מערכת שכוללת שני אתרים במצב
\( \psi = \frac{1}{\sqrt{2}} \left( |1\rangle + i|2\rangle \right) \).
בסעיף (1) של השאלה מניחים שלשני האתרים יש אותה אנרגיה פוטנציאלת (אפס),
ושתדירות הקפיצה ביניהם היא מספר ממשי
\( c \).
בסעיף (2) נזכרים שמודל של שני אתרים הוא מודל אפקטיבי.
למעשה, בשביל לקפוץ בין שני האתרים צריך לעבור דרך אתר אמצעי.
האתר האמצעי הוא בעל אנרגיה פוטנציאלית
\( \varepsilon_0 \),
ותדירות הקפיצה בינו לבין כל אחד משני האתרים הסמוכים הוא מספר ממשי
\( c_0 \).
(1) מה הוא הזרם
\( I(t) \)
שיוצא מאתר 1 כפונקציה של הזמן בהינתן הערך האפקטיבי
\( c \).
טיפ: כדי לפתור את השאלה אין צורך להתעסק עם אופרטור הזרם, אם כי זה יכול להועיל בהמשך לחשוב עליו...
(2) רשום את ההמילטוניאן של 3 האתרים בהינתן
\( c_0, \varepsilon_0 \).
(3) מה הן האנרגיות העצמיות ומה הם המצבים העצמיים של ההמילטוניאן?
טיפ: כדאי לעבור מבסיס
\( \{ 1,0,2 \} \)
לבסיס
\( \{ 0,+,- \} \),
ואז לבצע את הליכסון.
נוח להגדיר זוית
\( \theta \)
ובאמצעותה להביע את התשובה.
(4) רישמו ביטוי עבור ההסתברות
\( P_1(t) \)
למצוא את החלקיק באתר 1 כפונקציה של הזמן.
טיפ: רישמו את המצב התחילי בבסיס שמצאתם בסעיף הקודם, קדמו בזמן, ואז בצעו את ההטל.
(5) בהתבסס על הפתרון המדויק של סעיף 4, הגדירו את הערך האפקטיבי
\( c \)
באמצעות הפרמטרים שמתארים את המערכת המלאה.
הערה: התאור האפקטיבי מניח שהתדירות
\( \varepsilon_0 \)
היא גדולה ביחס לתדירות המעבר בין האתרים, ושמכשיר המדידה לא מסוגל לעשות רזולוציה שלה.
(6) בהתבסס על הפתרון המדויק של סעיף 4, מצאו ביטוי מקורב עבור הזרם בזמנים קצרים.
בפרט הבהירו מה זה זמן קצר, ומה הזרם בזמן אפס.
בנוסף נא צרפו ציור סכמטי של הזרם כפונקציה של הזמן (קו מקוקו - הפתרון האפקטיבי, קו רציף - הפתרון המדויק).
טיפ: כדי לפשט את האלגברה מותר לבצע את כל החישובים בסדר מוביל בצימוד
\( c_0 \).
exercise
(1360) מערכת עם שלושה אתרים, השרדות
2004A1
מערכת של שלושה אתרים מתוארת בבסיס הסטנדרטי
\( |x=-1\rangle, |x=0\rangle, |x=1\rangle \)
באמצעות ההמילטוניאן
\( H=\left(\array{0 & c & 1 \\ c & u & c \\ 1 & c & 0}\right) \)
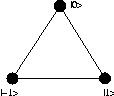
הנח שהאתר המרכזי
\( x=0 \)
מנותק (
\( c=0 \)
).
(א) רשום בבסיס הסטנדרטי את המצבים העצמיים
\( |S0\rangle, |S\rangle, |A\rangle \)
,
ואת האנרגיות העצמיות המתאימות.
(ב) רשום את ההמילטוניאן בבסיס החדש שמצאת לעיל.
להלן הנח שמתקיים
\( u=1 \)
, וכמו כן
\( c\ne0 \)
.
(ג) רשום את האנרגיות העצמיות
\( E_1, E_2, E_3 \)
,
ואת המצבים העצמיים
\( |E_1\rangle, |E_2\rangle, |E_3\rangle \)
של המערכת
כסופרפוזיציה של המצבים
\( |S0\rangle, |S\rangle, |A\rangle \)
.
(ד) רשום את מצבי האנרגיה לעיל גם בבסיס הסטנדרטי.
(ה) מה ההסתברות למצוא את החלקיק באתר
\( x=0 \)
לאחר פרק זמן
\( t \)
אם מכינים אותו בזמן
\( t=0 \)
במצב
\( |x=-1\rangle \)
.
(ו) מה ההסתברות למצוא את החלקיק באתר
\( x=0 \)
לאחר פרק זמן
\( t \)
אם מכינים אותו בזמן
\( t=0 \)
במצב
\( |A\rangle \)
.
exercise
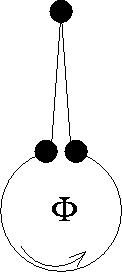
(1380) מערכת עם שלושה אתרים, השרדות וזרם
2005B1
נתונה מערכת בת שלושה אתרים (ראה שרטוט). היא מתוארת באמצעות ההמילטוניאן
\( H=\left(\array{2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 }\right) \)
באשר
\( x=\left(\array{0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 }\right) \)
(האתר השמאלי הוא
\( x=0 \)
העליון הוא
\( x=1 \)
והימני הוא
\( x=2 \)
).
נתון שמטען החלקיק שנע במערכת הוא
\( e \)
1. רשום את ההמילטוניאן המתקבל אם מוסיפים שטף מגנטי
\( \Phi \)
דרך הלולאה המחברת את האתר "האחרון" (הימני בשרטוט) לאתר "הראשון" (השמאלי).
2. הגדר את אופרטור הזרם באמצעות הנוסחא
\( I=-\left.\frac{dH}{d\Phi}\right|_{\Phi=0} \)
אופרטור זה נותן את הזרם דרך הלולאה. להלן אנו מניחים שהשטף המגנטי הוא אפס.
3. רשום בבסיס הסטנדרטי את המצבים העצמיים ואת האנרגיות העצמיות.
שימו לב שההמילטוניאן סימטרי להזזות כך שלא נדרש כאן "חישוב".
מכינים את החלקיק באתר "הראשון"
4. חשב את ההסתברות
\( p(t) \)
למצוא את החלקיק באתר "הראשון" לאחר פרק זמן
\( t \)
5. חשב את הזרם
\( \langle I \rangle_t \)
שזורם דרך הלולאה כפונקציה של הזמן.
exercise
(1390) מערכת עם ארבעה אתרים, זרם
2004B
נתונה מערכת בת ארבעה אתרים (ראה שרטוט). היא מתוארת באמצעות
ההמילטוניאן
\( H=\left(\array{0 & c_0 & 0 & c \\ c_0 & 0 & c & 0 \\ 0 & c & 0 & c_0 \\ c & 0 & c_0 & 0}\right) \)
נתון שמטען החלקיק שנע במערכת הוא
\( e \)
.
(1) רשמו את ההמילטוניאן המתקבל אם מוסיפים שטף מגנטי
\( \Phi \)
דרך הלולאה המחברת את שני האתרים הראשונים,
והגדירו בהתאם את אופרטור הזרם דרך לולאה זו.
להלן אנו מניחים שהשטף המגנטי הוא אפס.
(2) רשמו בבסיס הסטנדרטי את המצבים העצמיים ואת האנרגיות העצמיות כאשר
\( c=0 \)
.
השתמשו בסימון המתבקש (ימין/שמאל/סימטרי/אנטיסימטרי)
\( |SR\rangle, |SL\rangle, |AR\rangle, |AL\rangle \)
.
(3) רשמו את ההמילטוניאן המקורי
\( ( c{\ne}0, \,\, \Phi{=}0 ) \)
בבסיס החדש שמצאתם לעיל.
(4) רשמו את האנרגיות העצמיות
\( E_1, E_2, E_3, E_4 \)
,
ואת המצבים העצמיים
\( |E_1\rangle, |E_2\rangle, |E_3\rangle, |E_4\rangle \)
של המערכת
כסופרפוזיציה של המצבים
\( |SR\rangle, |SL\rangle, |AR\rangle, |AL\rangle \)
.
(5) רשמו את מצבי האנרגיה לעיל גם בבסיס הסטנדרטי.
(6) מכינים את החלקיק באתר מספר אחד:
\( | \Psi(t=0) \rangle = |1\rangle \)
חשבו את הזרם שזורם דרך הלולאה כפונקציה של הזמן
\( \langle I \rangle_t = \langle \Psi(t) | I | \Psi(t) \rangle \)
להלן סעיפי "בונוס" שלא ניכללו בגרסא המקורית של השאלה. בסעיפי הבונוס אתם מתבקשים לספק דרך אופציונלית לפתרון הבעיה שמאפשרת רישום של הפתרון by inspection ללא צורך בשום חישוב. טיפ: לצורך כך נוח לסמן את מצבי הבסיס בסימון
\( |x,y \rangle \)
(7) ההמילטוניאן הוא ספרבילי. רשמו אותו כסכום של שני איברים בצורה
\( H = H^{(x)} + H^{(y)} \)
(8) השתמשו בספרביליות כדי לרשום את המצבים העצמיים והאנרגיות העצמיות.
טיפ: זו למעשה אותה טכניקה שמשתמשים בה כדי לרשום מצבים עצמיים של חלקיק בקופסא מלבנית.
(9) השתמשו בספרביליות כדי לרשום את המצב
\( | \Psi(t) \rangle \)
על בסיס פתרון ידוע של בעית שני אתרים
(10) רישמו את הפתרון עבור הזרם by inspection
exercise
(1400) שני חלקיקים בשני אתרים, אוסצילציות
2005A1
נתונים שני חלקיקים שונים
\( a,b \)
בשני אתרים.
המערכת סימטרית לשיקוף מרחבי ואמפליטודת הקפיצה ליחידת זמן היא
\( \Delta \)
.
(ניתן להניח
\( \Delta \)
ממשי ללא הגבלת הכלליות).
הבסיס הסטנדרטי הוא:
\( |x_a,x_b\rangle = |1,1\rangle,\,\, |1,2\rangle,\,\, |2,1\rangle,\,\, |2,2\rangle \)
1. רשום את ההמילטוניאן
\( H \)
בבסיס הסטנדרטי.
שים לב שבצעד זמן אינפיניטסימאלי יכול לעבור לכל היותר חלקיק אחד מאתר לאתר.
ההסתברות למעבר סימולטני של שני חלקיקים היא אפס.
על מנת להקל על בדיקת התשובה נא להשתמש בבסיס על פי הסדר שהוגדר למעלה.
2. רשום את ההצגה המטריצית של האופרטור
\( T \)
שמחליף את שני החלקיקים.
3. הגדר סט של מצבים
\( | i=L,R,S,A \rangle \)
שבו
\( T_{ij} \)
אלכסוני.
בסעיף (3) הסימון מרמז מה היא התשובה ( שמאל, ימין, סימטרי, אנטיסימטרי).
הנח מעתה שמדובר בחלקיקם זהים בעלי ספין אפס (בוזונים!!).
4. רשום את ההמילטוניאן
\( H_{ij} \)
בבסיס
\( | i=L,R,S \rangle \)
5. רשום באותו בסיס את אופרטור השיקוף
\( R_{ij} \)
6. הגדר סט של מצבים שבו
\( R \)
מתלכסן.
7. מצא את המצבים העצמיים של ההמילטוניאן. רשום אותם בבסיס הסטנדרטי.
8. מה הן האנרגיות העצמיות?
מכינים בזמן
\( t=0 \)
את המערכת במצב הסימטרי
\( | S \rangle \)
9. מודדים את מספר החלקיקים באתר השמאלי. מה התוצאות האפשריות?
10
. מה זמן המחזור של האוסצילציות שעושה המערכת?
11
. מה התשובה לסעיף (9) אחרי חצי זמן מחזור?
exercise
(1430) ניסוי קונדסציה בשני אתרים
2006A1
בניסוי קונדסצית בוזה-אינשטיין מכינים מספר רב של חלקיקים במצב היסוד של "באר כפולה" סימטרית.
מצב זה מתואר על ידי פונקצית הגל
\( \Psi(x) = \exp\left(-\frac{(x+a)^2}{2\sigma^2}\right) + \exp\left(-\frac{(x-a)^2}{2\sigma^2}\right) \)
להשכלה כללית: אפשר למדוד את התפלגות התנע של החלקיקים באופן ניסיוני. לשם כך משחררים את הפוטנציאל, נותנים לחלקיקים לנוע באופן חופשי, ואז מצלמים אותם. באופן כזה התפלגות המהירויות של החלקיקים "מתורגמת" לתמונה מרחבית.
(1) רשום מה היא התפלגות התנע
\( P(k) \)
של החלקיקים המתוארים על ידי פונקצית הגל הנתונה. (אין צורך להקפיד על הנירמול הגלובאלי).
(2) הגדר באופן דומה את פונקצית הגל שמתארת מצב עצמי איזוגי לשיקוף, ורשום מה היא התפלגות התנע המתקבלת.
בסעיפים להלן יש לבצע את האנליזה המסגרת קרוב של "מערכת שני מצבים". נתון אמפליטודת המעבר
\( c \)
ליחידת זמן מבאר לבאר . בנוסף הניחו שיש לנסיונאי שליטה על הפרש הפוטנציאלים
\( u \)
בין שתי הבארות. להלן אתם מתבקשים לנתח שני "תסריטים" אפשריים.
תסריט ראשון:
יוצרים באופן פתאומי הפרש פוטנציאלים
\( u \)
גדול מאוד
\( (c \ll u) \)
. מחכים פרק זמן
\( t \)
ואז מודדים את התפלגות התנע של המערכת.
(3) מה תהיה התפלגות התנע של המערכת?
(4) מה צריך להיות שווה
\( t \)
על מנת שישארו מינימום חלקיקים בסביבת המערכת.
תסריט שני:
מדליקים את הפרש הפוטנציאלים לאט מאוד (באופן אדיאבטי) כך שלבסוף הוא גדול מאוד
\( (c \ll u) \)
. אז מאפסים אותו באופן פתאומי ומחכים פרק זמן
\( t \)
.
(5) מה תהיה התפלגות התנע של המערכת?
(6) מה צריך להיות שווה
\( t \)
על מנת שהתפלגות התנע תהיה גאוסית (בלי מודולציה).
התמרת פוריה של גאוסיאן:
\( FT\left[ \exp\left(-\frac{x^2}{2\sigma^2}\right) \right] \propto \exp\left(-\frac{\sigma^2 k^2}{2}\right) \)
exercise
(1470) מערכת עם שלושה אתרים, זרם
2007B1
חלקיק במערכת של שלושה אתרים מתואר בבסיס הסטנדרטי
\( |x=1\rangle, |x=2\rangle, |x=3\rangle \)
באמצעות ההמילטוניאן
\( H=\left(\array{0 & c & 0 \\ c & 0 & c \\ 0 & c & 0}\right) \)
(א) רשום את האנרגיות העצמיות
\( E_{0}, E_{+}, E_{-} \)
(ב) רשום בבסיס הסטנדרטי את המצבים העצמיים
\( |A\rangle, |S_{+}\rangle, |S_{-}\rangle \)
לחלקיק יש מטען
\( e \)
(ג) רשום את ההצגה המטריצית של אופרטור תצפית
\( I \)
עבור הזרם מאתר 1 לאתר 2.
(ד) מה הם ערכי התצפית האפשריים של אופרטור הזרם שהגדרת?
מכינים את החלקיק בזמן
\( t=0 \)
במצב
\( |x=1\rangle \)
(ה) מה ההסתברות למדוד
\( I=0 \)
לאחר פרק זמן
\( t \)
exercise
(1472) מערכת עם שלושה אתרים בטור, דינמיקה
2012A
חלקיק במערכת של שלושה אתרים מתואר בבסיס הסטנדרטי
\( |1\rangle, \ |2\rangle, \ |3\rangle \)
באמצעות ההמילטוניאן
\( H=\left(\array{0 & c_a & 0 \\ c_a & 0 & c_b \\ 0 & c_b & 0}\right), \ \ \ \ \ \ \ c_a=c\cos(\theta), \ \ c_b=c\sin(\theta) \)
מכינים את החלקיק בזמן
\( t=0 \)
באתר הראשון.
את התשובות בטא באמצעות
\( c, \ \ \theta \)
.
לשם פתרון סעיף (1) יש למצוא את שורשי הפולנום האופיני (משוואה מאוד פשוטה).
(1) מצא את האנרגיות העצמיות
\( E_0, \ \ E_{+}, \ \ E_{-} \)
(2) רשום בבסיס הסטנדרטי את המצבים העצמיים
\( |0\rangle, \ \ |+\rangle, \ \ |-\rangle \)
(3) רשום בבסיס האנרגיה את המצב התחילי
(4) רשום ביטוי עבור
\( P(t) \)
, ההסתברות למציאת החלקיק באתר הראשון לאחר פרק זמן
\( t \)
(5) רשום ביטוי עבור
\( I(t) \)
, ערך התצפית של הזרם שנמדד מאתר 2 לאתר 3 בזמן
\( t \)
exercise
(1480) מערכת של שני QBITS, תורת הפרעות
2007A1
QUBIT הוא התקן בעל שני מצבי בסיס
\( |x=0\rangle, |x=1\rangle \)
הנח ששני המצבים הם בעלי אותה אנרגיה ושאמפליטודת המעבר ביניהם היא
\( c \)
.
נתונה מערכת הכוללת שני QUBITs בעלת מצבי בסיס
\( |x_a,x_b\rangle \)
.
מתברר שכאשר שני ה-QUBITs במצב
\( x=1 \)
, יש לכך תשלום אנרגטי
\( u \)
.
את ההמילטוניאן של המערכת נרשום בצורה
\( H = H_0+uV \)
(1) רשום את היצוג המטריצי של
\( V \)
בבסיס הסטנדרטי (סעיף זה אינו דורש עבודה אלגברית).
ההמילטוניאן
\( H_0 \)
הוא אלכסוני בבסיס מסוים. סמן את מצבי הבסיס בסימון
\( |SS\rangle, |SA\rangle, |AS\rangle, |AA\rangle \)
.
(2) רשום וקטורי עמודה המיצגים את מצבי הבסיס החדשים בבסיס הסטנדרטי.
(3) רשום את המטריציה האלכסונית שמיצגת את
\( H_0 \)
בבסיס שהגדרת (סעיף זה אינו דורש עבודה אלגברית).
(4) רשום בבסיס החדש את מטריצת ההפרעה
\( V \)
(5) מצא את האנרגיות העצמיות של המערכת עד סדר ראשון באינטרקציה.
(6) מצא את אנרגית מצב היסוד עד סדר שני באינטראקציה.
ההגדרה של אופרטור התנע
exercise
(1660) צומת גוזפסון וזרם גוזפסון
2009B
קבל מורכב משני לוחות סופר-מוליכם.
בסופר מוליך נושאי המטען הם "זוגות קופר" אליהם ניתן להתיחס כאל
בוזונים
בעלי מטען
\( e^* = 2e \)
.
במצב ניטרלי
\( |n{=}0\rangle \)
חלק מהזוגות מצויים בלוח השמאלי וחלק בלוח
הימני.
המצב הטעון
\( |n\rangle \)
מתקבל על ידי העברת
\( n \)
זוגות מהלוח השמאלי אל הלוח הימני.
הבסיס לתאור המערכת הוא אוסף המצבים
\( |n\rangle \)
עם
\( n=\text{integer} \)
.
מגדירים אופרטור "הזזה" בצורה
\( D|n\rangle = |n+1\rangle \)
.
הנח שאמפליטודת המעבר (ליחידת זמן) של זוג מלוח ללוח (באמצעות מינהור)
היא
\( \Omega \)
.
בנוסף הנח שהקיבול של הקבל הוא
\( C \)
.
בסעיף 4 הנח שמכינים את המערכת במצב
\( |n{=}0\rangle \)
והשתמש בתורת הפרעות לאבולוציה-בזמן סדר ראשון.
בסעיפים 5-6 יש להסתייע בתמונה הקלאסית של האבולוציה במרחב הפאזות.
-
הגדר את המצב העצמי
\( |\varphi\rangle \)
של
\( D \)
בעל הערך העצמי
\( \exp(-i\varphi) \)
.
-
רשום את ההמילטוניאן של המערכת תוך שימוש באופרטורים הצמודים
\( n,\varphi \)
.
-
הגדר את אופרטור הזרם
\( I \)
כמשתמע מהנוסחא עבור
\( d\langle n \rangle / dt \)
-
מה ההסתברות למצוא את המערכת לאחר זמן קצר במצב
\( |n{\ne}0\rangle \)
-
מה תדירות התנודות הקטנות
\( \omega \)
של המערכת?
-
באיזה מצבי
\( |n\rangle \)
סביר למצוא את המערכת לאחר זמן רב?
מצבים סטציונריים של חלקיק בקופסא
exercise
(2120) חלקיק קשור על ידי פונקצית דלתא
חלקיק ממוקם בתוך בור פוטנציאל אינסופי באינטרוול
\( [-a,a] \)
אשר במרכזו פוטנציאל דלתא
\( V(x)=-u\delta(x) \).
1. מה פונקצית הגל ומה האנרגיה של המצב הקשור עבור בור ברוחב אינסופי.
2. מיצאו את פונקצית הגל ואת המשוואה שקובעת את האנרגיה של מצב היסוד עבור רוחב בור סופי.
3. מהו
\( u_c \)
כך שעבור
\( u > u_c \)
מתקבל מצב יסוד קשור בעלי אנרגיה שלילית?
4. מה פונקצית הגל של מצב היסוד עבור
\( u = u_c \)
exercise
(2122) מצב קשור באתר שמצומד למוליך חד מימדי
2012A
בבעיה זו נדרש למצוא את אנרגית המצב הקשור E של חלקיק במערכת שכוללת אתר
המצומד למוליך חד מימדי.
החלקיק הוא בעל מסה M. המוליך החד מימדי הוא אינסופי
\( x\in[-\infty,\infty] \)
.
האתר שבו קשור החלקיק מצוי בסמיכות לנקודה
\( x_0 \)
.
אילו האתר היה מופרד מהמוליך אנרגית הקשר של החלקיק היתה
\( E_0 \)
.
בפועל האתר מצומד למוליך, וההמילטוניאן הוא
\( H = H_{free} \,+\, |0\rangle E_0\langle 0| \, +\, |x_0 \rangle \lambda \langle 0| \, +\, |0 \rangle \lambda \langle x_0| \)
where \( H_{free} \) is the Hamiltonian of a free particle along the wire.
ההצגה הסטנדרטית של פונקצית הגל בבסיס המקום היא
\( \Psi \mapsto (\psi_0, \psi(x)) \)
באשר האמפליטודות הן
\( \psi_0 = \langle 0|\Psi\rangle, \ \ \ \ \psi(x) = \langle x|\Psi\rangle \)
עם קונבנצית נירמול
\( |\psi_0|^2+\int_{-\infty}^{\infty} |\psi(x)|^2 dx =1 \)
(1) רשום בהצגה הסטנדרטית את
\( \langle 0 |H| \Psi \rangle \)
.
(2) רשום בהצגה הסטנדרטית את
\( \langle x|H| \Psi \rangle \)
.
רשום את מערכת המשוואות
\( H |\Psi\rangle = E |\Psi\rangle \)
בהצגה מרחבית.
טיפ: הטל על המצבים
\( \langle 0|, \ \ \langle x| \)
והשתמש בתוצאות הסעיפים הקודמים.
על ידי חילוץ הראה שמקבלים משוואה סגורה עבור
\( \psi(x) \)
עם פוטנציאל אפקטיבי
\( V(x;E) \ \ = \ \ u(E) \ \delta(x-x_0) \)
שים לב שבשלב זה אנו מתיחסים לאנרגית הקשר E כאל נתון ידוע.
טיפ: ללא הגבלת הכלליות אפשר להניח שהמיקום
\( x_0 \)
הוא ראשית מערכת הצירים.
(3) רשום את הביטוי עבור
\( u(E) \)
(4) רשום משוואה עבור אנרגית הקשר
\( E \)
(5) פתור את המשוואה במקרה הפרטי
\( E_0=0 \)
טרנספורמציות, אינוריאנטיות, סימטריות
תורת פיזור (אלמנטרי)
exercise
(2550) פיזור על ידי פונקציות דלתא במימד אחד
שאלה זו היא שאלת פוקוס על חומר שמוצג בסעיף 39.2 ובסעיף 44.1 של תקצירי ההרצאה. שימו לב שיש קונבנציות שונות לרישום מטריצת הפיזור (מבחינת מיספור ערוצי הפיזור והסימנים של מקדמי המעבר וההחזרה). להלן נבחר להשתמש בקונבנציה של נוסחא 39.19 שמקובלת ברוב הספרים האלמנטריים.
התיחסו לפיזור של חלקיק בעל אנרגיה
\( E \)
על פוטנציאל
\( V(x)=u\delta(x) \).
-
מיצאו את מקדמי ההחזרה והמעבר של מחסום הדלתא. שימו לב שבבררת המחדל היא להגדיר את אמפליטודות הכניסה והיציאה של פונקצית הגל בנקודות שקרובות אינפיניטסימלית למחסום.
-
רישמו את מטריצת הפיזור
\( S \)
-
מה תהיה מטריצת הפיזור אם אמפליטודות הכניסה והיציאה מאזור הפיזור מוגדרות בנקודות
\( x=-L_1 \ \text{and} \ x= +L_2 \).
שימו לב שאם מחברים את נקודות הקצה של אזור הפיזור, אז מתקבלת טבעת שאורכה
\( L = L_1+L_2 \).
-
מגדירים את ההתנגדות של מחסום בצורה
\(R = (1-g)/g \).
מה תהיה ההתנגדות השקולה של שני מחסומים בטור, שההתנגדויות שלהן
\( R_1,R_2 \)
ושהמרחק ביניהם אפס.
-
רישמו ביטוי עבור מקדם המעבר של שני מחסומי דלתה בטור, שהמרחק ביניהם
\( a \).
את בעיה זו, הידועה בשם Fabry Perrot interference, אפשר לפתור בשיטה של Transfer Matrix, אבל יותר פשוט לפתור אותה כבעיית התאבכות שדורשת ביצוע של סכום על מסלולים. ראו פתרון בסעיף 44.1 של תקצירי ההרצאה. שימו לב שבאנרגיות מסוימות העבירות היא 100% בניגוד לאינטואיציה.
exercise
(2552) מטריצת פיזור של צומת I
שלשה חוטים מחוברים בנקודה אחת. נניח כי אות המגיע מרגל אחת מתפזר בחלקו
לרגליים האחרות ומוחזר בחלקו לרגל ממנו הוא בא. נתון שהמערכת סימטרית
לפרמוטציה של החוטים.
נסמן ב
\( S \)
את מטריצת הפיזור. זוהי מטריצה
\( 3\times 3 \)
.
-
רשום\י את
\( S \)
אם נתון שכל האמפליטודות ההחזרה שוות לאותו מספר ממשי
\( r \)
, וכל אמפליטודות המעבר שוות לאותו מספר ממשי חיובי
\( t \)
.
-
קבע\י את הערכים המספריים של
\( r \)
ושל
\( t \)
.
-
הכלל את הנוסחא למקרה שבו יש יותר משלושה חוטים.
exercise
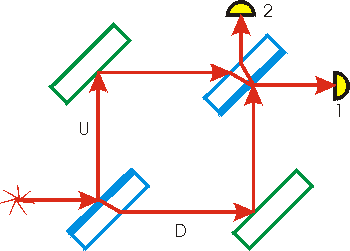
(2660) אינטרפרומטר Mach-Zehnder
רשום מטריצת פיזור 4x4 אשר מתארת מראה חצי מחזירה.
נתונים מקדם ההעברה
\( T \)
ומקדם ההחזרה
\( R \)
של מראה כזאת.
שים לב שאת אמפליטות הפיזור המתאימות
\( t, r \)
אפשר להגדיר באמצעות "שורש ריבועי".
אבל יש לקחת בחשבון שיש גם פאזה, שאם לא לוקחים אותה בחשבון מאבדים אוניטריות.
הסבר מדוע מבחינה פורמאלית אפשר להתייחס למראה כזאת
כאילו מדובר בבעית פיזור של צומת דו-ערוצית עם מטריצת פיזור 2x2
אינטרפרומטר Mach-Zehnder מורכב משתי מראות חצי מחזירות ומשתי מראות רגילות.
למראה רגילה יש מקדם החזרה השווה לאחד כך שהאפקט היחיד הוא שינוי כיוון הקרן ושינוי
\( \pi \)
בפאזה.
אלומת החלקיקים מתפצלת במראה החצי מחזירה הראשונה לשתי אלומות שעוברות שני מסלולים אופטיים שונים,
כך שנצבר הפרש פאזה
\( \phi \)
. אז הן מתאחדות שוב במראה החצי מחזירה השניה,
והחלקיקים יכולים לצאת באחד משני הערוצים.
רשום ביטויים עבור מקדמי המעבר לכל אחד משני הערוצים.
ודא שסכום הסתברויות המעבר הוא אחד.
תורת פיזור: שיטת היסטי הפאזה
חלקיק בגאומטרית אהרונוב-בוהם (טבעת)
exercise
(3060) סוספטיבליות מגנטית של טבעת
2012A
הנח\הניחי אלקטרון בעל מסה
\( m \)
, מטען
\( e \)
, ויחס גירומגנטי g בטבעת חד מימדית בעלת אורך
\( L \)
.
הטבעת מצויה בשדה מגנטי אחיד. השטף דרך הטבעת הוא
\( \Phi = [L^2/(4\pi)]\mathcal{B} \)
.
המערכת הוכנה בטמפרטורה אפס, ז"א שהיא מצויה במצב היסוד.
המגנטיזציה M של המערכת מוגדרת דרך הנגזרת הראשונה של האנרגיה לפי השדה המגנטי.
הסוספטיביליות
\( \chi \)
של המערכת מוגדרת דרך הנגזרת השניה של האנרגיה בשדה שואף לאפס.
שים לב שאלקטרונים הם פרמיונים בעלי ספין חצי המקיימים את עקרון האיסור של פאולי.
-
מצא\י את הסוספטיבליות המגנטית של המערכת עבור אלקטרון יחיד.
-
הסבר\הסבירי באיזה מובן האפקט הוא דיאמגנטי.
-
מה יהיה האפקט של נוכחות מפזר על התוצאה שמצאת.
-
חזור על סעיף (1) עבור 3 אלקטרונים.
-
במקרה האחרון - מה המגנטיציה של המערכת בשדה שואף לאפס.
-
כיצד היתה משתנה תשובתך אם השטף המגנטי היה מרוכז במרכז הטבעת.
exercise
(3070) מגנטיזציה של טבעת עם אלקטרונים
2009A
טבעת בעלת רדיוס
\( R \)
מצויה בשדה מגנטי אחיד
\( B \)
.
בטבעת יש 5 אלקטרונים בעלי מסה
\( M \)
מטען
\( e \)
וספין חצי.
איבר האינטראקציה של הספין עם השדה הוא
\( g \frac{e}{2m} B S_z \)
באשר
\( S_z=\pm 1/2 \)
.
שים לב ששני אלקטרונים לא יכולים לאכלס את אותו מצב.
נסמן את אנרגית מצב היסוד ב-
\( E \)
נגדיר את המגנטיזציה בצורה
\( \tilde{M}(B)=-dE/dB \)
נתונים:
\( R, \ M, \ e, \ g\approx2.0023, \ B \)
אם לא היה לאלקטרונים ספין אז המגנטיזציה היתה פונקציה מחזורית, עם
מחזור
\( B_0 \)
.
בהמשך השאלה אנו מניחים שהשדה המגנטי הוא
\( B=\ell B_0 + \Delta B \)
באשר
\( \ell \)
מספר שלם ובאשר
\( 0< \Delta B \ll B_0 \)
-
רשום ביטוי עבור
\( B_0 \)
-
מצא את
\( \tilde{M}(B) \)
עבור
\( \ell=0 \)
כאשר
\( \Delta B \rightarrow 0 \)
-
בהמשך לסעיף הקודם רשום את התוספת ל-
\( \tilde{M}(B) \)
עבור
\( \Delta B \)
קטן
-
מצא את
\( \tilde{M}(B) \)
עבור
\( \ell \)
גדול כאשר
\( \Delta B \rightarrow 0 \)
-
בהמשך לסעיף הקודם רשום את התוספת ל-
\( \tilde{M}(B) \)
עבור
\( \Delta B \)
קטן
-
הגדר מה זה
\( \ell \)
גדול
טיפ: בסעיפים 2,4 כדאי לצייר דיאגרמת איכלוס של רמות האנרגיה.
חלקיק בשדה מגנטי אחיד
exercise
(3520) חלקיק בטבעת עם שדה מגנטי לא הומוגני
2013A
חלקיק בעל מסה
\( M \)
, מטען
\( e \)
, וספין חצי עם קבוע גירמגנטי
\( g \)
מצוי בטבעת בעלת רדיוס
\( R \)
.
יוצרים שדה מגנטי לא הומוגני
\( B(r,\varphi,z)=br^{\alpha} \)
בכיוון ציר
\( z \)
.
בנוסף מניחים מטען
\( Q \)
במרכז הטבעת.
1. רשום ביטוי עבור הוקטור פוטנציאל שמופיע בהמילטוניאן של החלקיק
2. רשום את ההמילטוניאן
\( H = h(L_z, S_z; M, e, g, R, b, \alpha,Q) \)
כולל אינטראקצית ספין-מסילה
3. רשום מה הקבוע הגירומגנטי האפקטיבי
\( g_L \)
שמשתמע מאיבר זימן האורביטלי בהמילטוניאן שרשמת.
4. מה צריך להיות רדיוס הטבעת על מנת שאיבר זימן האורביטלי לא ישפיע על הספקטרום.
טיפ:
את התנאי בסעיף 4 אפשר לקבל ללא צורך במציאת ההמילטוניאן.
exercise
(3560) חלקיק בפוטנציאל הרמוני דו-מימדי עם שדה מגנטי
חלקיק קשור על ידי פוטנציאל הרמוני דו מימדי
\( V(r)=\frac{1}{2} m \Omega^2 r^2 \)
-
מה הן רמות האנרגיה? מה הניוון של כל רמה?
הדרכה: נוח לענות על שאלה זו על ידי הפרדת משתנים בקואורדינטות קרטזיות (
\( E_{n_1,n_2} = ??? \)
).
בשלב שני יש "לתרגם" את התוצאה לשפה של קואורדינטות פולריות (
\( E_{m,\nu} = ??? \)
).
השלב השני (אשר נדרש לצורך פתרון המשך השאלה) דורש חשיבה "בלתי קונבנציונלית" ולא עבודה שחורה!
-
מוסיפים שדה מגנטי הומוגני
\( B \)
. מה הן רמות האנרגיה?
-
מה הניוון הגנרי של כל רמה אם מזניחים את האיבר הדיאמגנטי?
-
מה הסוספטיבליות המגנטית אם המערכת היא במצב היסוד?
בסעיפים לעיל התבקשת להניח שתנועתו של החלקיק מוגבלת להיות על פני מישור דו-מימדי.
חזור על הסעיפים הנ"ל במקרה התלת מימדי (ז"א החלקיק יכול לנוע גם בכיוון האנכי).
exercise
(3570) חלקיק בעיגול עם שדה מגנטי - רמות לנדאו
-
רשום בקואורדינטות קרטזיות את ההמילטוניאן של חלקיק במישור XY בנוכחות שדה מגנטי הומוגני אנכי .
-
הראה שההמילטוניאן הוא כמו של אוסצילטור דו-מימדי פלוס איבר זימן.
-
רשום את ההמילטוניאן בקואורדינטות פולריות, וציין מה היא המשוואה הרדיאלית.
-
מה הן רמות האנרגיה שמתקבלות מהמשוואה הרדיאלית ללא איבר זימן? מה הניוון של כל רמה?
-
מה הן רמות האנרגיה שמתקבלות מהמשוואה הרדיאלית עם איבר זימן? מה הניוון של כל רמה?
הערות:
-
בסעיף 4 אפשר להסיק את התשובה מתוך הכרות עם הפתרון הידוע בקואורדינטות קרטזיות.
-
בסעיף 5 הנח שתנועתו של החלקיק מוגבלת בתוך עיגול בעל רדיוס R.
-
יש להראות שהתשובות הסופיות הן בהתאמה לתוצאות הידועות עבור רמות לנדאו.
exercise
(3610) אלקטרון בגאומטריה של אפקט הול
הנח\הניחי דגם דו-מימדי באורך
\( L \)
, עם תנאי שפה מחזוריים באינטרוול
\( 0 < x < L \)
.
נתון פוטנציאל חשמלי
\( V(x,y)=\frac{1}{2} \alpha y^2 \)
, ויש שדה מגנטי הומוגני
\( B \)
בכיוון ציר
\( z \)
.
נוח להביע את השדה המגנטי באמצעות הגודל חסר המימד
\( b = B/\sqrt{m\alpha} \)
.
ניתן לשים לב ש-
\( b \)
הוא למעשה יחס בין שתי תדירויות (מה הן?).
לתוך הדגם מכניסים
\( N \)
אלקטרונים חסרי ספין.
הראה שכל עוד
\( N < [ 4 (1+b^2)^3 m\alpha ] ^{1/4} L/\pi \)
רק פס (band) לנדאו הראשון מאוכלס.
(לצורך קבלת תוצאה זו יש לעשות לא מעט אלגברה).
הראה\י כיצד ניתן לקבל בקלות יחסית את התוצאה הנ"ל בקרובים של שדה מגנטי חזק מאוד ושל שדה מגנטי חלש מאוד.
exercise
(3640) אלקטרונים בבור פוטנציאל סופי + שדה מגנטי
2005C3
נתון בור פוטנציאל דו מימדי בגודל
\( L \times L \)
, ובעומק
\( V_0 \)
.
זה אומר
\( V(x)=V_0 \)
בתוך הבור, קירות מאוד גבוהים בהיקף הבור, וכן
\( V(x)=0 \)
מחוץ לבור.
כתוצאה מכך כל האלקטרונים עם אנרגיה
\( 0<E \)
בורחים החוצה.
הנח שהאלקטרונים שנותרים בקופסא הם חסרי ספין, בעלי מסה
\( m \)
, ובעלי מטען
\( e \)
.
1. רשום את התנאי
\( L_{min}<L \)
לכך שיוכל להיות לפחות אלקטרון אחד בבור.
להלן הנח
\( L_{min} \ll L \)
.
2. חשב את מספר האלקטרונים
\( N_0 \)
שיכולים להיות בבור.
יוצרים שדה מגנטי הומוגני
\( B \)
במאונך למישור שבו מצוי הבור.
בסעיפים להלן ניתן להשתמש (ללא צורך בהוכחה) בתוצאות ידועות לגבי רמות לנדאו.
3. מצא את השדה המקסימאלי
\( B=B_2 \)
כך שיש שתי רמות לנדאו מלאות בתוך הבור.
נסמן את מספר החלקיקים בסעיף (3) בסימון
\( N_2 \)
4. למה שווה היחס
\( N_2/N_0 \)
?
5. הכלל את התוצאה למקרה של n רמות לנדאו מלאות.
הדרכה:
תנאי השפה בקצות הבור הם בעלי השפעה זניחה על הספקטרום,
כך שניתן להשתמש בתוצאות ידועות שנגזרות מהפתרון של לנדאו.
exercise
(3710) אלקטרון בגאומטריה של אפקט הול, באר כפולה
2013B
נתון דגם מלבני דו מימדי ארוך. במימד האורכי
\( 0 < x < L \)
הניחו תנאי שפה מחזוריים.
הדגם מצוי בשדה מגנטי אנכי
\( \vec{B} = (0,0,B(y)) \)
.
רוחב הדגם מאפשר איכלוס של 3 אלקטרונים חסרי ספין ברמת לנדאו התחתונה.
כל אלקטרון הוא בעל מסה
\( m \)
ומטען
\( e \)
.
בסעיפים 1-3 הניחו שדה הומוגני
\( B(y)=B_0 \)
בכיוון ציר Z.
בסעיפים 4-6 הניחו שהפכו את כיוון השדה המגנטי בחצי המישור התחתון
\( B(y<0)=-B_0 \)
(1) רישמו את ההמילטוניאן של אלקטרון בדגם זה.
(2) רישמו את הפוטנציאל האפקטיבי
\( V^{\ell}(y), \, [\ell=0,\pm] \)
שמתקבל לאחר הפרדת משתנים.
(3) רישמו את פונקציות הגל
\( \Psi^{0,\pm}(x,y) \)
של שלושת האלקטרונים.
הניחו שריצפת הפוטנציאל שטוחה כך ששלושת המצבים מנוונים באנרגיה.
(4) רישמו וציירו סכמטית את הפוטנציאלי האפקטיבי
\( V^{\text{eff}}(y) \)
עבור כל אחד משלושת האלקטרונים בשדה המגנטי החדש.
(5) רישמו ביטויים מקורבים עבור פונקציות הגל החדשות.
(6) רישמו על סמך WKB ביטוי עבור פיצול האנרגיה
\( \Delta=C\exp(-A) \)
של המצבים החדשים.
הדרכה:
יש להביע את התשובות באמצעות הנתונים.
על מנת לפשט ביטויים מותר ורצוי להשתמש בסימון
\( \omega_B=eB_0/m \)
.
כמו כן מותר ורצוי להשתמש בסימון
\( \varphi _0(r) = (m\omega_B/\pi)^{1/4}\exp(-\frac{1}{2}m\omega_B r^2) \)
בסעיף 6 יש לספק ביטויים מפורשים עבור A, C
בחישוב A יש להזניח את האנרגיה הקינטית ביחס לגובה המחסום.
חבורות לי, יוצרים, אלגברת לי
בניית ההצגות של חבורת הסיבובים
סיבובים - ספינים
exercise
(4420) זיהוי מצב קיטוב של "ספין 1/2"
זהה\זהי בשתי דרכים את האורינטציה של המצב המקוטב:
\( \exp(-i \pi / 4) \cos(\pi/8) | \uparrow \rangle + \sin (\pi/8) | \downarrow \rangle \)
-
הדרך הראשונה היא על ידי קבלתו ממצב UP באמצעות מטריצות סיבוב (סביב Y ואח"כ סביב Z).
-
הדרך השניה היא על ידי חישוב של וקטור הפולריזציה (ז"א חישוב ערכי תוחלת).
exercise
(4430) זיהוי סיבוב Hadamard של ספין 1/2
2005C2
נתון חלקיק בעל ספין חצי. מגדירים את הפעולה הבאה (בבסיס הסטנדרטי):
\( R=\frac{1}{\sqrt{2}}\left(\array{1 & 1 \\ 1 & -1 }\right) \)
שאלות לחימום:
1. מפעילים את
\( R \)
על מצב
UP
. מה יהיה כיוון הקיטוב?
2. מפעילים את
\( R \)
על מצב
DOWN
. מה יהיה כיוון הקיטוב?
שאלת "מיליון הדולר":
3. מה זוית הסיבוב המיוצג על ידי
\( R \)
ניתן לממש את
\( R \)
במעבדה עלי ידי הפעלת שדה לפרק זמן של
\( 1sec \)
ההמילטוניאן בעת הפעלת השדה הוא מהצורה
\( H=h\cdot\sigma+c \)
4. קבע את הכיוון ואת הגודל של השדה המגנטי
\( h \)
5. קבע את הערך של הקונסטנטה
\( c \)
exercise
(4440) זיהוי סיבובים
2008A2
נתון חלקיק בעל ספין חצי. מגדירים את מטריצות הסיבוב הבאות (בבסיס הסטנדרטי):
\( R_A=\left(\array{0 & 1 \\ 1 & 0 }\right) \)
\( R_B=\frac{1}{\sqrt{2}}\left(\array{1 & -1 \\ 1 & 1 }\right) \)
\( R_C=\frac{1}{\sqrt{2}}\left(\array{1 & 1 \\ 1 & -1 }\right) \)
(א) עבור כל אחת מהמטריצות הנתונות זהה את זוית הסיבוב
\( \Phi \)
ואת ציר הסיבוב
\( \vec{n} \)
(ב) רשום מטריצת סיבוב 4x4 אשר מבצעת את הפעולה
\( R_C \)
על שני ספינים.
exercise
(4482) מערכת עם שלושה אתרים, אנלוגיה לבעית פרסציה
2015A
מערכת שמאופינת על ידי ספקטרום-אנרגיה לא מנוון
\( E_n \)
. מכינים את מערכת במצב
\( \psi \)
.
נתונות ההסתברויות
\( p_n = |\langle E_n | \psi \rangle|^2 \)
שמאפינות את המצב התחילי.
\( P(t) \)
היא ההסתברות למצוא את המערכת במצב התחילי
לאחר פרק זמן
\( t \)
.
מגדירים
\( \bar{P} = \lim_{t\rightarrow\infty} \ \frac{1}{t}\int_0^t P(t) \)
(0) הביעו את
\( \bar{P} \)
באמצעות ההסתברויות
\( p_n \)
חלקיק בעל מטען
\( q \)
מצוי במערכת חד מימדית עם שלושה אתרים.
הבסיס הסטנדרטי הוא
\( |x=1\rangle, \ |x=0\rangle, \ |x=-1\rangle \)
, וההמילטוניאן הוא
\( H_0=\left(\array{0 & c & 0 \\ c & 0 & c \\ 0 & c & 0}\right) \)
מוסיפים שדה חשמלי
\( f \)
בכיוון ציר X.
המצב התחילי של החלקיק הוא
\( |x=1\rangle \)
(1) רישמו את ההמילטוניאן המתקבל באמצעות היוצרים
\( S_x,S_y,S_z \)
של ספין1
(2) מה התדירות הבסיסית
\( \omega \)
של התנודה המחזורית שתתקבל במערכת?
(3) את ההסתברות
\( P(t) \)
אפשר לרשום כסכום פוריה של פונקציות סינוס
וקוסינוס.
רישמו ביטוי שכולל את האיברים שאינם אפס. אין צורך לחשב את המקדמים.
(4) השתמשו בתוצאה של סעיף (0) על מנת לקבל ביטוי מפורש עבור
\( \bar{P} \).
מה אפשר להגיד על המקדמים בסעיף (3) בלי לעשות עבודה אלגברית?
(5) מה הערך המינמילי של
\( \bar{P} \)?
באיזה שדה הוא מתקבל?
(6) רשמו ביטוי מפורש עבור
\( R(t) = \langle x \rangle_t \)
בסעיף (4) ניתן ורצוי להשתמש בנוסחאות ידועות עבור מצבי קיטוב של ספין1.
בסעיף (6) ניתן ורצוי להשתמש בתוצאות ידועות לגבי פרסציה (נוסחת רבי).
exercise
(4484) ספין בשדה מגנטי מסתובב
2017A
ההמילטוניאן של ספין 1/2 בשדה מגנטי הוא
\( H=h(t) \cdot S \)
.
השדה המגנטי גודלו
\( |h(t)| = \Omega_0 \)
,והוא מסתובב
במישור XY בתדירות זויתית
\( \omega \)
,
כך שהזוית שהוא יוצר עם ציר X אחרי זמן
\( t \)
היא
\( \varphi=\omega t \)
.
לשם פתרון שאלה זו ניתן להשמש בקביעה שההמילטוניאן של הספין
במערכת צירים מסתובבת הוא
\( \tilde{H} = H - \omega S_z \)
-
מצא את זוית הנטיה
\( \theta_0 \)
שבה צריך להכין את הספין אם רוצים שהוא יעקוב בזוית קבועה אחרי השדה המסתובב.
(הזוית נמדדת ביחס לכיוון האנכי כנהוג עבור קואורדינטות כדוריות.)
מכינים (בזמן אפס) את הספין בכיוון ציר X
-
מה היא הסטיה הזויתית המכסימאלית
\( \Delta \theta \)
של הספין מכיוון השדה במהלך האבולוציה
נותנים לשדה לעשות חצי סיבוב.
-
מה יהיה הכיוון הסופי של הספין במערכת המעבדה בגבול
\( \omega \rightarrow 0 \)
-
מה יהיה הכיוון הסופי של הספין במערכת המעבדה בגבול
\( \omega \rightarrow\infty \)
-
עבור איזה ערכים של
\( \omega \)
הסטיה של הספין מכיוון
השדה היא
אפס בסוף התהליך?
טיפ: שאלה זו אינה מצריכה עבודה אלגברית אלא רק הבנה גאומטרית /
פיסיקלית.
exercise
(4510) הפעלת מטריצות סיבוב על ספינים
2002A2
מצא את וקטור המצב
\( \Psi_m \)
בבסיס הסטנדרטי עבור ספין המקוטב במישור XY בזוית
\( \varphi=60^o \)
.
התיחס למקרים הבאים:
-
ספין חצי
-
ספין 1 עם קיטוב מעגלי
-
ספין 1 עם קיטוב לינארי
את האלמנטים של וקטור המצב בתשובה הסופית יש לנסח באמצעות
\( \sqrt{2}, \ e^{i \pi/\mbox{integer}} \)
וכיו"ב.
על מנת למנוע אפס נקודות בגין שגיאה אלגברית נא לרשום את נוסחת החישוב + התוצאה הסופית.
exercise
(4520) הפעלת מטריצות סיבוב על ספינים
2007B3
נתון ספין חצי
במצב
\( | \psi \rangle = \exp(-i \pi/4) \cos(\pi/8)|\uparrow \rangle + \sin(\pi/8)|\downarrow \rangle \)
.
(1) זהה את האורינטציה
\( (\theta,\varphi) \)
של מצב הקיטוב המיוצג על ידי
\( |\psi \rangle \)
.
(2) רשום את
\( |\psi \rangle \)
באמצעות מטריצות סיבוב
\( R_y,R_z \)
הפועלות על
\( |\uparrow \rangle \)
(3) רשום את נוסחת החישוב + ביטווים מפורשים עבור המטריצות
\( R_y,R_z \)
נתון ספין 1 במצב של קיטוב מעגלי בכיוון ציר Z
(4) רשום את המצב המתקבל לאחר סיבוב באותן זויות כמו בסעיף 1.
(5) רשום את ההסתברות למדוד מצב של קיטוב לינארי בכיוון ציר Z (לאחר הסיבוב הנ"ל).
מותר להשתמש בתוצאות ידועות עבור היוצרים.
exercise
(4530) הפעלת מטריצות סיבוב על ספינים
2004B2
(א) רשום את ההצגה הסטנדרטית של ספין 1 עם קיטוב לינארי בכיוון ציר z.
(ב) חשב את ההצגה הסטנדרטית של ספין 1 עם קיטוב מעגלי בכיוון ציר x.
מודדים האם יש לספין קיטוב לינארי בכיוון ציר y.
(ג) מה ההסתברות לתוצאה חיובית עבור ההכנה של סעיף (א)?
(ד) מה ההסתברות לתוצאה חיובית עבור ההכנה של סעיף (ב)?
סיבובים - פונקציות גל
exercise
(4620) סיבוב של פונקצית גל
חלקיק מתואר באמצעות פונקצית הגל:
\( \psi(\vec{r}) = f(r) \left( \sqrt{2} \sin \theta \cos \phi + \cos \theta \right) \)
מסובבים את פונקצית הגל בזווית של
\( 90^{\circ} \)
סביב ציר
\( y \)
, ואחר כך בזווית של
\( 90^{\circ} \)
סביב ציר
\( z \)
.
מה פונקצית הגל המתקבלת? פתור בשתי דרכים שונות:
הדרך הפשוטה היא לעבור לקואורדינטות קרטזיות, ולפעול עם מטריצת סיבוב אוקלידית (מרחבית) על הקואורדינטות.
הדרך הארוכה היא לרשום את פונקצית הגל כסופרפוזיציה של פונקציות
\( Y^{lm}(\theta,\phi) \)
,
ולהפעיל על וקטור המקדמים מטריצות סיבוב בהצגה הסטנדרטית.
exercise
(4622) פרסציה שנגרמת על ידי סדרת פולסים
2017B
נתון ספין חצי שעליו מפעילים סדרת פולסים מגנטיים. ההמילטוניאן הוא
\( \mathbf{h}(t)\cdot \mathbf{S} \)
משך של כל פולס הוא
\( \tau \)
, וגודלו הוא
\( h \)
.
השדה במשך הפולס הראשון הוא בכיוון Z, במשך הפולס השני הוא בכיוון Y, וחוזר חלילה.
כתוצאה מסדרה זו של פולסים נוצרת תנועת פרסציה בתדירות
\( \Omega \)
מסביב לציר
\( \mathbf{n} \)
(1) רשום ביטוי עבור תדירות הפרסציה
\( \Omega \)
(2) מצא את ציר הסיבוב
\( \mathbf{n} \)
(וקטור יחידה)
(3) רשום את
\( \Omega\rightarrow\Omega_0 \)
בגבול שבו ההינע הוא סדרת פולסים עם
\( \tau\rightarrow0 \)
.
(4) רשום את
\( \mathbf{n}\rightarrow\mathbf{n}_0 \)
בגבול שבו ההינע הוא סדרת פולסים עם
\( \tau\rightarrow0 \)
.
(5) רשום ביטוי עבור
\( \tan{\theta} \)
של הזוית בין
\( \mathbf{n}_{\ } \)
לבין
\( \mathbf{n}_0 \)
הערות:
על פי הגדרה תדירות הפרסציה היא
\( \Omega = \phi/(2\tau) \)
באשר
\( \phi \)
היא זוית הסיבוב השקולה במהלך שני פולסים עוקבים.
התשובות לסעיפים 3,4 הן טריויאליות. אפשר לנחש אותן.
הביטויים בסעיפים 2,5 לאחר פישוט כוללים פונקצית tan בלבד.
ביטוי לא מפושט לא יקבל ניקוד.
exercise
(4640) תנע זויתי של פונקצית גל
2009B
פונקצית הגל של חלקיק היא
\( \Psi(x,y,z)=f(r)z(z+1) \)
-
רשום את פונקצית הגל בהצגה
\( |r \theta \phi \rangle \)
-
רשום את פונקצית הגל בהצגה
\( |r \ell m \rangle \)
נתון
\( Y^{00}=\sqrt{\frac{1}{4\pi}}, \, Y^{10}=\sqrt{\frac{3}{4\pi}}\cos\theta, \, Y^{20}=\sqrt{\frac{5}{16\pi}}(3\cos^2\theta-1) \)
מגדירים
\( M_n = \int_0^{\infty} r^n (f(r))^2 dr \)
-
רשום תנאי על
\( M_4, M_6 \)
כך שפונקצית הגל תהיה מנורמלת.
להלן נתון שמתקיים
\( M_6 = 5 / (8\pi) \)
-
מה היא ההסברות למצוא את החלקיק במצב "כדורי" (
\( \ell=0 \)
)
-
מה הם הערכים האפשריים שניתן לקבל (בהסתברות>0) במדידה של
\( L_x \)
-
כנ"ל אם מודדים את
\( L_z \)
-
מה היא ההסתברות למצוא את החלקיק במצב "פולרי" (
\( \ell=1 \)
) עם
\( L_x=1 \)
רמז לסעיף האחרון: בחישוב מופיע פקטור
\( \langle \uparrow | \leftrightarrow \rangle \)
exercise
(4710) חלקיק על קליפה כדורית, דינמיקה
2005B2
נתונה קליפה כדורית בעלת רדיוס
\( R \)
וחלקיק בעל מסה
\( M \)
ומטען .
\( e \)
בשאלה זו עליך להניח שניתן לעורר את החלקיק מרמת היסוד לרמת האנרגיה הראשונה,
אך לא מעבר לכך. מכאן שמרחב המצבים הוא ארבע מימדי.
מכינים את החלקיק כך שהוא "מרוכז" ככל האפשר "בקוטב הצפוני" של הקליפה.
1. רשום את פונקצית הגל
\( \Psi(\theta,\varphi) \)
של החלקיק.
הסעיף הזה דורש "חשיבה". התשובה היא פשוטה ואינה מצריכה "אלגברה".
המצב שרשמתם אינו מצב סטציונרי.
החלקיק יבצע תנודות בין הקוטב הצפוני לבין הקוטב הדרומי.
2. מה זמן המחזור של התנודות?
מגדירים את הקיטוב של המערכת בצורה הבאה:
\( P(t)= \langle \Psi(t) | \hat{z} | \Psi(t) \rangle \)
3. מצא את הקיטוב
\( P(t) \)
כפונקציה של הזמן.
נתון:
\( Y_{00} = \frac{1}{\sqrt{4\pi}}, \,\,\,\,\,\, Y_{10}(\theta,\varphi)= \sqrt{\frac{3}{4\pi}}\cos\theta, \,\,\,\,\,\, Y_{1,\pm1} \propto \sin(\theta) \)
exercise
(4720) חלקיק על קליפה כדורית, פולס
2005A
נתונה קליפה כדורית בעלת רדיוס
\( R \)
וחלקיק בעל מסה
\( M \)
ומטען .
\( e \)
בזמן
\( t=-\infty \)
מניחים את החלקיק על פני הקליפה במצב האנרגיה הכי נמוך.
מדליקים פולס של שדה חשמלי בכיוון ציר Z שגודלו
\( \mathcal{E}(t) = \mathcal{E}_0 e^{-\frac{1}{2}(t/\tau)^2} \)
להלן הנח תקפות של תורת הפרעות סדר ראשון
-
רשום ביטוי מפורש עבור פוטנציאל ההפרעה
\( W(\theta,\varphi) \)
-
חשב את אלמנטי המטריצה של
\( W \)
בין מצב היסוד למצבים המעוררים.
-
מה הפרש האנרגיה של המעברים המותרים מרמת היסוד?
-
חשב את ההסתברות למצוא את החלקיק ברמה מעוררת לאחר שהפולס מסתיים
(זה
אומר לאחר פרק זמן ארוך מאוד כשהשדה כבר שווה לאפס).
נתון:
\( FT[e^{-\frac{1}{2}(t/\tau)^2}]=\sqrt{2\pi}\tau e^{-\frac{1}{2}(\tau\omega)^2} \)
\( Y_{00} = \frac{1}{\sqrt{4\pi}}, \,\,\,\,\,\, Y_{10}(\theta,\varphi)=\sqrt{\frac{3}{4\pi}}\cos\theta \)
exercise
(4730) חלקיק על קליפה כדורית, דינמיקה
2007A
נתונה קליפה כדורית בעלת רדיוס
\( R \)
וחלקיק בעל מסה
\( M \)
ומטען
\( e \)
.
שים לב שמשתני התצפית הסטנדרטיים שמתארים את מצב החלקיק הם
\( (\theta,\varphi,L_x,L_y,L_z) \)
.
בשאלה זו עליך להניח שניתן לעורר את החלקיק מרמת היסוד לרמת האנרגיה
הראשונה,
אך לא מעבר לכך. מכאן שמרחב המצבים הוא ארבע מימדי.
סמן את מצבי הבסיס בסימון
\( |0\rangle, |\uparrow\rangle, |\updownarrow\rangle,|\downarrow\rangle \)
.
מכינים את החלקיק כך שהוא "מרוכז" ככל האפשר "בקוטב הצפוני" של
הקליפה.
החלקיק מבצע תנודות בין הקוטב הצפוני לבין הקוטב הדרומי.
(1) מה האנרגיה של כל אחד ממצבי הבסיס. הגדר את מצב היסוד כאנרגיה אפס.
(2) רשום את פונקצית הגל
\( \Psi(\theta,\varphi) \)
של החלקיק בזמן
\( t=0 \)
.
(3) מה זמן המחזור
\( T_0 \)
של התנודות?
(4) מוסיפים למערכת הבלתי מופרעת שדה מגנטי אחיד
\( \mathcal{B} \)
בכיוון ציר X.
רשום את איבר ההפרעה (של זימן) באמצעות משתני התצפית הסטנדרטיים.
מצא ערך של
\( \mathcal{B} \)
שגורם לכך שבזמן
\( T_0/2 \)
החלקיק חוזר למצב התחילי.
(5) מוסיפים למערכת הבלתי מופרעת שדה חשמלי אחיד
\( \mathcal{E} \)
בכיוון ציר Z.
רשום את איבר ההפרעה (של סטארק) באמצעות משתני התצפית הסטנדרטיים.
מצא את זמן המחזור
\( T \)
של התנודות.
נתון:
\( Y^{00} = \frac{1}{\sqrt{4\pi}},\,\,\,\,\,\, Y^{10} = \sqrt{\frac{3}{4\pi}}\cos\theta,\,\,\,\,\,\, Y^{1,\pm1} \propto \sin(\theta) \)
סעיפים (2) ו-(4) דורשים "חשיבה". התשובה היא פשוטה ואינה מצריכה
"אלגברה".
חיבור תנע זויתי
exercise
(4828) מצב של ספין שמהווה חלק מסינגלט או טריפלט
נתון שהכינו מערכת שכוללת שני ספינים במצב סינגלט או באחד ממצבי הטריפלט:
\( |\uparrow\downarrow\rangle- |\downarrow\uparrow\rangle; \,\,\,|\uparrow\uparrow\rangle, \,\,\,|\uparrow\downarrow\rangle+ |\downarrow\uparrow\rangle, \,\,\,|\downarrow\downarrow\rangle \)
(1) מה ההסתברות למדוד את שני הספינים עם אותו קיטוב X בכל אחד מהמקרים?
(2) מה ההסתברות למדוד את אחד הספינים (נניח הראשון) עם קיטוב בכיוון ציר X
(3) מה הוא וקטור הפולריציה \( \vec{M} \) שמתאר את כל אחד משני הספינים?
וקטור הפולריזציה מוגדר בצורה הבאה: \( \vec{M} = (\langle \sigma_x \rangle, \langle \sigma_y \rangle , \langle \sigma_z \rangle) \)
את ערכי התוחלת קיבעו על בסיס ההסתברויות למדידת ספין עם כיוון קיטוב X,Y,Z.
כדי לחסוך עבודה שחורה מיותרת שימו לב שלמצבים יש סימטריה אזימוטלית
(הסבירו מדוע המצבים נשארים אותו דבר אם מסובבים אותם סביב ציר Z).
exercise
(4850) מצב שזור של שני ספינים
2006B2
נתונים שני חלקיקים בעלי ספין חצי. מצבי הספין של המערכת מיוצגים
בבסיס הסטנדרטי
\( |\uparrow\uparrow\rangle, |\uparrow\downarrow\rangle, |\downarrow\uparrow\rangle, |\downarrow\downarrow\rangle \)
הכינו את המערכת במצב
\( |\Psi\rangle \propto |\uparrow\uparrow\rangle + |\uparrow\downarrow\rangle + |\downarrow\uparrow\rangle \)
שים לב שהמערכת הוכנה במצב סימטרי ביחס לפרמוטציה כך שלשני החלקיקים יש אותו מצב קיטוב.
(1) מצא את היצוג של האופרטור
\( S_x \)
שמתאר את הספין של אחד החלקיקים כמטריצה
בבסיס הסטנדרטי
שהוגדר לעיל.
(2) מצא את וקטור הפולריזציה
\( \vec{M} = (\langle S_x \rangle, \langle S_y \rangle , \langle S_z \rangle ) \)
שמתאר את מצב הקיטוב של כל אחד מהחלקיקים.
(3) רשום את כיוון הקיטוב
\( \vec{n} \)
ואת מידת הקיטוב
\( p=|\vec{M}| / M_{max} \)
של המצב החד חלקיקי.
(4) מה הוא וקטור המצב בבסיס
up / down
שמתאר ספין יחיד עם קיטוב מלא בכיוון
\( \vec{n} \)
(5) מה יהיה מצב המערכת אם מכינים את שני החלקיקים במצב של קיטוב מלא בכיוון
\( \vec{n} \)
.
בסעיף האחרון רשום את התשובה כוקטור עמודה
בבסיס הסטנדרטי
כפי שהוגדר בראשית השאלה.
כל התשובות צריכות להיות מוגמרות (אל תצפו שהבודק יבצע חישובים בשבילכם).
exercise
(4853) דינמיקה של ספינים מצומדים
2015B
נתונים שני ספינים מצומדים המתוארים על ידי ההמילטוניאן
\( H=\mu S^A \cdot S^B + hS_z^A \)
באשר
\( \vec{S}=\frac{1}{2}\vec{\sigma} \)
.
מכינים את הספין הראשון במצב קיטוב Z.
נתמקד
להלן בתנועה של הספין השני (
\( S^B \)
).
את מצב הספין מתארים על ידי וקטור פולריזציה
\( \vec{M} = (\langle \sigma_x^B \rangle, \langle \sigma_y^B \rangle, \langle \sigma_z^B \rangle) \)
.
1. רשום את ההמילטוניאן של המערכת בבסיס הסטנדרטי
מכינים את הספין השני במצב קיטוב X
2. מה תהיה תדירות התנועה שלו בגבול
\( h\rightarrow\infty \)
3. מה תהיה תדירות התנועה שלו בגבול
\( h\rightarrow0 \)
מכינים את הספין השני במצב קיטוב Z- (ספין down)
4. מה תהיה תדירות התנועה - נתונים
\( \mu, h \)
5. רשום ביטוי מפורש עבור וקטור
הפולריזציה
\( \vec{M}(t) \)
6. מה התנאי לכך שהקיטוב של הספין לא יתאפס במהלך האבולוציה?
חיבור תנע זויתי (מתקדם)
exercise
(4872) המומנט המגנטי של הפרוטון
2021B
המצב הספיני של מערכת הכוללת שלושה קוורקים מתוארת בהצגה הסטנדדטית
\( 2 \otimes 2 \otimes 2 \).
הפרוטון הוא חלקיק שמורכב משלושה קוורקים (קוורקים הם חלקיקי דירק, ז"א פרמיונים עם ספין חצי).
לצורך השאלה אפשר לרשום את המצב שנקרא "פרוטון מקוטב" בצורה
\( |p \uparrow \rangle = |uud \rangle \otimes | SpinState \rangle \)
המטען
\( q \)
של הקוורקים u ו-d הוא בהתאמה 2/3 ומינוס 1/3 ממטען הפרוטון, והמסה של קווארק היא בקרוב שליש מהמסה של הפרוטון.
משיקולי סימטריה נובע שהמצב הספיני של הפרוטון הוא מצב ספין חצי עם סימטריה זוגית להחלפת u.
טיפ: יש להתיחס לקביעה זו כאל נתון. מכאן נובע שנוח לבצע את הפרוק בסדר הבא
\( (2 \otimes 2) \otimes 2 \).
כאשר שמים חלקיק דירק בשדה מגנטי בכיוון ציר Z האנרגיה שלו היא
\( E = -g \frac{q}{2M} S_z B \equiv -\mu B \)
כאשר שמים פרוטון בשדה מגנטי הנוסחא דומה אבל עם מקדם אחר
\( g_p \)
שאותו אנו רוצים לחשב.
בסעיפים (3) ו-(4) הביעו את התשובה באמצעות
\( \mu_u, \mu_d \).
(1) מה הפרוק של מרחב מצבי הספין? רישמו את התשובה כסכום ישר של מימדי הצגות בלתי פריקות.
(2) מה המצב הספיני של הפרוטון - רישמו כסופרפוזיציה של מצבים בבסיס הסטנדרטי.
(3) מה ההסתברות למצוא את הפרוטון (לדוגמה) במצב
\( | \uparrow \uparrow \downarrow \rangle \),
ומה תהיה האנרגיה שלו במצב כזה?
(4) הביעו את המומנט המגנטי של הפרוטון
\( \mu_p \)
כקומבינציה לינארית של
\( \mu_u \)
ושל
\( \mu_d \).
(5) בהתבסס על הנתונים לגבי המטען והמסה של הקוורקים קיבעו מה הוא המקדם \( g_p \).
אופרטורים וקטוריים, אפקט זימן
אינטראקצית ספין-מסילה
exercise
(5662) רמות לנדאו בגרפין
2010A
ההמילטוניאן האפקטיבי של אלקטרון בשכבה דו מימדית של גרפין הוא
\( H = v_0 \sigma \cdot (p-eA) \)
באשר
\( \sigma=(\sigma_x,\sigma_y,0) \)
ובאשר A הוא הוקטור פוטנציאל עבור שדה אנכי B בכיול לנדאו.
שים לב שהבסיס הסטנדרטי להצגת האלקטרון הוא
\( |x,y,m\rangle \)
באשר
\( m=\uparrow,\downarrow \)
(1) בהעדר שדה מגנטי, עבור תנע נתון
\( p=(p_x,p_y) \)
,
מה הן האנרגיות העצמיות של החלקיק?
(2) בכיול לנדאו האופרטור
\( \hat{Y}=-(1/eB)\hat{p}_x \)
הוא קבוע תנועה.
רשום את ההמילטוניאן
\( H^{Y} = H_{m,m'}(p_y,\,y-Y) \)
שמתקבל לאחר הפרדת משתנים.
כדאי לזכור שקומבינציה לינארית של קואורדינטות קנוניות
\( a=(sQ+iP/s)/\sqrt{2} \)
זה אופרטור הורדה,
ולרשום את המטריצה המתקבלת בצורה האלטרנטיבית
\( H_{m,m'}(a,a^{\dag}) \)
(3) הגדר את האופרטור
\( C = (H^{Y})^2 \)
רשום מה הם הערכים העצמיים
\( \lambda_{n=0,1,2,...} \)
של C
שים לב שכל הערכים העצמיים למעט
\( n=0 \)
הם מנוונים.
(4) כיוון ש C הוא קבוע תנועה ניתן לבצע הפרדת משתנים נוספת.
רשום את המטריצה 2x2 שמיצגת את
\( H^{Y,n} \)
(5) מצא את רמות האנרגיה
\( E_{Y,n,\pm} \)
עבור
\( n>0 \)
.
(6) מצא את המצבים העצמיים, ורשום אותם בבסיס הסטנדרטי.
שים לב שהמצב הקוונטי בבסיס הסטנדרטי מיוצג באמצעות
\( \Psi \mapsto (\psi_{\uparrow}(x,y),\psi_{\downarrow}(x,y)) \)
ניתן להשתמש בסימון
\( \varphi^{n}() \)
עבור הפונקציות העצמיות של אוסצילטור הרמוני חד מימדי.
exercise
(5664) אינטראקצית ספין-מסילה
2008B
אלקטרון בעל מסה
\( M \)
ומטען
\( e \)
מצוי בטבעת חד מימדית בעלת רדיוס
\( R \)
.
לאלקטרון אינטראקצית ספין-מסילה עם השדה החשמלי שיוצר מטען
\( Q \)
הממוקם במרכז הטבעת.
מומלץ להשתמש ביחידות
\( \hbar=c=1 \)
(א) רשום את ההמילטוניאן
\( H(x,p,S) \)
של האלקטרון
(ב) מה הן האנרגיות העצמיות של האלקטרון?
(ג) מה המהירות של האלקטרון בכל אחד ממצבי האנרגיה?
(ד) איזה שטף מגנטי
\( \Phi \)
דרך מרכז הטבעת יאפס את האפקט של
\( Q \)
על אלקטרון בעל ספין up
נא להביע את כל התשובות באמצעות הנתונים בלבד.
exercise
(5666) חלקיק בקופסא דו-מימדית עם מדרגת פוטנציאל
2016A
אלקטרון בעל מסה
\( M \)
מצוי בתוך קופסא דו מימדית
\( |x|<a, \ \ |y|<b \)
.
בתוך הקופסא יוצרים מדרגת פוטנציאל
\( V(x)=\frac{1}{2}V_0 \ \text{sgn}(x) \)
.
בשאלה זו עליך לקחת בחשבון אינטראקצית ספין-מסילה. יחידות
\( c=1, \ e=1, \ g\approx2 \)
(1) רשום את ההמילטוניאן באמצעות אופרטורי המקום והתנע, ואופרטור הספין
\( \sigma_z \)
(2) רשום את המצבים העצמיים הבלתי-מופרעים
\( |n,m\rangle \)
בבסיס הסטנדרטי.
(3) רשום ביטוי עבור אלמנטי המטריצה
\( \langle n,m|V(x)|1,1\rangle \)
(4) חשב את התיקון מסדר-שני של אנרגית מצב היסוד שנובע מהאינטראקציה
האלקטרוסטטית
(5) אילו מצבים עצמיים אינם מושפעים מאינטרקצית ספין-מסילה?
(6) חזור על סעיף (3) עבור אינטראקצית ספין-מסילה.
(7) חזור על סעיף (4) עבור אינטראקצית ספין-מסילה.
טיפ: השתמש בתשובותיך בסימונים הבאים:
\( \text{SIN}_{\nu}(\theta)=cos(\nu\theta) \ \text{for} \ \nu=1,3,... \)
\( \text{SIN}_{\nu}(\theta)=sin(\nu\theta) \ \text{for} \ \nu=2,4,... \)
\( c_{\nu} = \int_0^{\pi/2}\sin(\nu\theta)\cos(\theta) d\theta \)
מצב הספין
\( \sigma_z \)
הוא "מספר קוונטי טוב" - התיחסות אליו נדרשת
רק בתשובה לסעיף 6.
התשובה לסעיפים (4) ו-(7) היא טור. יש לציין בברור על מה מתבצע הסכום.
exercise
(5668) פרסציה של ספין בגין אינטראקצית ספין מסילה
2010B
אלקטרון בעל מסה M מטען e וספין עם קבוע גירומגנטי g,
משוגר עם אנרגיה E בתוך מוליך חד מימדי בכיוון ציר X.
המוליך עובר דרך לוחות קבל שאורכו L.
הקבל יוצר שדה חשמלי
\( \mathcal{E} \)
בכיוון ציר Y.
כמו כן באותו איזור יש שדה מגנטי
\( \mathcal{B} \)
בכיוון ציר Z.
כאשר האלקטרון נכנס לאיזור האינטראקציה הספין שלו מקוטב בכיוון התנועה.
בכל הסעיפים להלן הניחו שאפשר להתעלם מההסתברות לכך שהחלקיק יוחזר מאזור האינטראקציה.
כמו כן הניחו שאפשר להשתמש בקרוב מסדר אפס
\( v \approx (2E/M)^{1/2} \)
עבור המהירות של החלקיק שמופיעה באיבר הספין-אורביט.
(1) מה יהיה הכיוון
\( \varphi \)
של הספין ביציאה מאזור האינטראקציה. בססו את התשובה על זמן המעוף דרך המערכת.
(2) מה צריך להיות
\( \mathcal{B} \)
על מנת שהספין לא יסתובב.
בסעיפים להלן עליכם לתת תשובה יותר מדויקת על סמך אנרגית השיגור של החלקיק.
נוח לקבוע
\( x=0 \)
בתור הקואורדינטה של נקודת הכניסה.
(3) רישמו את מצב החלקיק באזור האינטראקציה בבסיס הסטנדרטי
\( |x,m\rangle \)
באשר
\( m=\uparrow,\downarrow \)
(4) בהתבסס על הסעיף הקודם, תנו תשובה לסעיף הראשון.
(5) בונוס: תנו תשובה מדויקת יותר אם לא עושים קרוב סדר אפס עבור המהירות באיבר הספין-אורביט.
תורת הפרעות למצבים קונטיים קשורים
exercise
(6030) טבעת דיסקרטית עם מחסום פוטנציאל
2021A
נתונה שרשרת בעלת
\( N \)
אתרים, המסומנים באמצעות האינדקס
\( x \).
תדירות הקפיצה בין אתרים היא
\( c \).
יוצרים מחסום על ידי כך שיוצרים באתר
\( x=0 \)
פוטנציאל
\( u \).
(1) הסבירו בצורה מדויקת את המשפטים הבאים: אם הפוטנציאל מאוד מאוד "גדול" אפשר להתיחס לטבעת "המנותקת" כאל שרשרת עם
\( N{-}1 \)
אתרים; השרשרת היא למעשה גרסא דיסקרטית של "בור פוטציאל חד מימדי".
(2) רישמו מה הן האנרגיות העצמיות והמצבים העצמיים המנורמלים של הטבעת במקרים הקיצוניים של פוטנציאל אפס, ופוטציאל מאוד גדול.
(3) הסבירו את ההבדל בספקטרום בין מספר אתרים זוגי ואיזוגי. הדגימו עבור
\( N = 3,4\).
(4) בהמשך לסעחף הקודם, חשבו בתורת הפרעות עד סדר שני את התיקון לספקטרום של הטבעת במקרה של פוטנציאל חלש.
(5) הגדירו מה זה פוטנציל "חלש". שרטטו שירטוט סכמטי של האנרגיות כפונקציה של הפוטנציאל (אינטרפולציה ביו "חלש" לבין "גדול").
exercise
(6040) קופסא דו מימדית עם קיר מוזז, תורת הפרעות
2010B
נתון חלקיק בעל מסה M בקופסא דו-מימדית ריבועית
\( x,y\in[0,a] \)
בעלת צלע a.
ההזזה של הקיר השמאלי מתוארת על ידי הפונקציה
\( x=\epsilon(y) \)
.
אילו הקופסא היתה חד מימדית איבר ההפרעה בהמילטוניאן היה
\( \langle \varphi |V | \psi \rangle =\left(\frac{\epsilon}{2M}\right) \left[ \frac{\partial\varphi}{\partial x}\right]\left[\frac{\partial\psi}{\partial x}\right] \)
באשר אנו מניחים הזזה קטנה, והנגזרות מחושבות בנקודה
\( x=0 \)
.
(1) רשום את ההכללה הדו-מימדית של הנוסחא לעיל (דורש הבנה בלבד).
הנח שהקיר מוטה בזוית קטנה כך שמתקיים
\( \epsilon(0)=-\epsilon_0/2 \)
וכן
\( \epsilon(a)= +\epsilon_0/2 \)
(2) רשום את מטריצת ההמילטוניאן עבור שלושת המצבים הנמוכים ביותר (בבסיס הלא מופרע).
(3) רשום את התיקון המוביל לאנרגית מצב היסוד.
(4) רשום את התיקון המוביל לאנרגיות של המצבים המעוררים.
נתון:
\( \int_0^{\pi/2}\cos(u)\sin(2u)udu = \frac{4}{9} \)
exercise
(6050) חלקיק מופרע בקופסה ריבועית
2009A
נתון חלקיק חסר ספין בעל מסה
\( M \)
בקופסה ריבועית
\( x,y \in [-a,a] \)
בהמשך השאלה מוסיפים הפרעה
\( u\delta(x)\delta(y) \)
-
רשום את פונקציות הגל
\( \psi(x,y) \)
של מצב היסוד הבלתי מופרע
-
כנ"ל גם את 3 המצבים המעוררים הנמוכים ביותר שמצומדים על ידי ההפרעה למצב היסוד.
-
רשום את ההמילטוניאן
\( H=H_0+V \)
כסכום של שתי מטריצות
\( 4\times 4 \)
בבסיס הנ"ל
-
רשום את המצבים העצמיים (כוקטורי עמודה) ואת האנרגיות העצמיות בסדר ראשון ב-
\( u \)
-
חשב את התיקון מסדר שני ב-
\( u \)
לאנרגית מצב היסוד.
exercise
(6070) חלקיק בטבעת + פוטנציאל, תורת הפרעות
2007B
נתונה חלקיק בעל מסה
\( M \)
ומטען
\( e \)
בטבעת חד מימדית בעלת רדיוס
\( R \)
.
בתור "הפרעה" יוצרים שדה חשמלי
\( \mathcal{E} \)
הומוגני במקביל למישור הטבעת.
1. רשום את ההמילטוניאן
\( \mathcal{H}(\theta,p) \)
של המערכת.
2. איזה סימטריות יש למערכת בלי/עם הפרעה.
3. רשום את ההצגה המטריצית של ההמילטוניאן בבסיס המתאים לטיפול הפרעתי.
4. חשב את אנרגית מצב היסוד
\( n=0 \)
עד סדר שני בהפרעה.
5. חשב את אנרגית המצבים המעוררים
\( n>1 \)
עד סדר שני בהפרעה.
exercise
(6080) חלקיק בעל ספין בקופסא + מפזר
2003B3
אלקטרון בעל ספין
\( 1/2 \)
ומסה
\( M \)
, מצוי בבור פוטנציאל חד מימדי.
הנח תנאי שפה אפס בקצות האינטרוול
\( -L/2 < x < L/2 \)
.
ההמילטוניאן של המערכת הוא
\( H=\frac{p^2}{2m}+\epsilon\delta(x)(1/2+S_z) \)
.
(א) רשום את האנרגיות ואת המצבים העצמיים (בהצגה הסטנדרטית) כאשר
\( \epsilon=0 \)
.
(ב) חשב את התיקון מסדר ראשון לאנרגיות העצמיות עבור
\( \epsilon \)
קטן. האם נותר ניוון בספקטרום?
(ג) רשום את האנרגיות העצמיות של החלקיק כאשר
\( \epsilon \to \infty \)
. ציין והסבר את הניוון בספקטרום.
(ד) צייר (באופן איכותי) את האנרגיות של 8 המצבים הנמוכים ביותר כפונקציה של
\( \epsilon \)
.
exercise
(6120) אוסצילטור הרמוני + הפרעה
נתון אוסצילטור הרמוני בעל תדירות
\( \omega \)
.
מוסיפים להמילטוניאן הפרעה מהצורה
\( H_I = \lambda x \)
.
מצא\י את האנרגיה של מצב היסוד עד סדר שני, על-פי תורת ההפרעות, וע"י פתרון מדויק.
השווה\השווי בין התוצאות.
במקום ההפרעה בסעיף הראשון מוסיפים הפרעה מהצורה:
\( H_I = \lambda x^4 \)
.
מהו התיקון ברמת האנרגיה ה-
\( n \)
עד סדר ראשון?
exercise
(6140) הפרעה שוברת סימטריה, הסרת ניוונים
2005A3
נתון חלקיק בעל ספין 2 המתואר על ידי ההמילטוניאן
\( H \,\,=\,\, 2J_3^2+J_1^2+J_2^2 \,+\, 2\lambda (J_1^2-J_2^2) \)
קל מאוד להיווכח שההמילטוניאן עם
\( \lambda=0 \)
הוא אלכסוני בבסיס הסטנדרטי
-
מה הן האנרגיות העצמיות (ללא הפרעה)?
-
שרטט דיאגרמה של רמות האנרגיה והמחש באמצעותה אילו מצבים ההפרעה מצמדת.
-
חשב את המצבים העצמיים ואת האנרגיות העצמיות של הרמה המעוררת הראשונה.
-
חשב עד סדר שני את ההיסט של הרמה התחתונה.
exercise
(6150) הפרעה שוברת סימטריה , הסרת ניוונים
2005B3
נתון חלקיק בעל ספין 1 המתואר על ידי ההמילטוניאן
\( H \,\,=\,\, 2S_x^2-4S_y^2+6S_z^2 \,-\, hS_z \)
בשלושת הסעיפים הראשונים הנח
\( h=0 \)
מגדירים את אופרטורי ההיטל
\( P_i = \hat{1}-S_i^2 \)
-
על איזה מצב מתבצעת "ההטלה" של (לדוגמה) האופרטור
\( P_z \)
-
מה הם המצבים העצמיים של ההמילטוניאן (רשמו אותם בבסיס הסטנדרטי)?
-
מה הן האנרגיות העצמיות?
מוסיפים שדה מגנטי
\( h \)
בכיוון ציר Z.
לשם פשטות הרישום בלענו בתוך ההגדרה של
\( h \)
את כל המקדמים.
-
רשמו את איבר האינטראקציה בבסיס הסטנדרטי.
-
רשמו את ההמילטוניאן (כולל איבר האינטראקציה) בבסיס של סעיף (2).
-
מה הן האנרגיות העצמיות של ההמילטוניאן?
-
ציירו ציור סכמטי של האנרגיות כפונקציה של השדה
\( h \)
.
הכינו את החלקיק במצב של קיטוב לינארי בכיוון ציר Z.
הדליקו את השדה מגנטי בצורה אדיאבטית כך שבסופו של דבר
\( 1 \ll h \)
.
בגלל בעיות במעבדה השדה המגנטי היה מוטה במקצת ביחס לכיוון האנכי.
-
מה המצב של הספין בסוף התהליך?
exercise
(6210) אפקט שטרק באטום המימן
2011A
האלקטרון באטום המימן הוא חלקיק בעל מסה M ומטען e שרואה פוטנציאל
\( V(r)=-\alpha/r \)
. להלן נניח שההסתברות למצוא את החלקיק ברמת אנרגיה מעוררת
\( 2<n \)
היא זניחה כך שמרחב המצבים של החלקיק הוא בעל מימד 5, ונפרס על ידי שני
אורביטלים כדוריים ושלושה אורביטלים פולריים כך שהבסיס להצגה הוא
\( |s1\rangle, |s2\rangle, |px\rangle, |py\rangle, |pz\rangle \)
. אנו מזניחים את אינטראקצית
ספין-מסילה כך שאפשר להתעלם מהספין. את האטום שמים בשדה חשמלי אחיד
\( \mathcal{E} \)
בכיוון ציר Z, וכתוצאה מכך הוא מתקטב. מטרת השאלה היא חישוב הפולריזציה של האטום
\( \tilde{P}(\mathcal{E})=e\langle z \rangle \)
. את
התשובות יש לבטא באמצעות
\( (M,a,e,\mathcal{E},c_1,c_2) \)
באשר
\( a=1/(\alpha M) \)
הוא רדיוס האטום של בוהר, ובאשר
\( c_1 =8\sqrt{2}/9, \ \ c_2=3\sqrt{3} \)
. יש להתיחס להנחיות שבסוף השאלה ולהמנע מעבודה שחורה.
-
רישמו את ההמילטוניאן בצורה הסטנדרטית באמצעות המשתנים הדינמיים
\( H(p_r,L,r,\theta; \mathcal{E}) \)
-
רישמו את שתי המטריצות שמיצגות את ההמילטוניאן הבלתי מופרע, ואת האינטראקציה עם השדה החשמלי.
-
רישמו את הביטוי לאנרגית מצב היסוד
\( E_{gr}(\mathcal{E}) \)
בקרוב של תורת הפרעות סדר שני.
-
רישמו את הביטוי לאנרגית המצב המעורר הנמוך
\( E_{ex}(\mathcal{E}) \)
-
רישמו את הביטוי עבור הפולריזציה של האטום אם הכינו אותו במצב היסוד
-
רישמו את הביטוי עבור הפולריזציה של האטום אם הכינו אותו ברמה המעוררת
את הפונקציות הרדיאליות של האלקטרון באטום המימן ניתן לרשום באופן
\( \frac{1}{a^{3/2}}R^{\ell\nu}\left(\frac{r}{a} \right) \)
,
באשר
\( R^{01}=2e^{-x}, \ \ R^{02}=\frac{1}{\sqrt{6}}\left(\frac{x}{2}\right)e^{-x/2}, \ \ R^{11}=\frac{1}{\sqrt{2}}\left(1-\frac{x}{2}\right)e^{-x/2} \)
.
הנחיות: בסעיף 2 מופיעים שני אינטגרלים רדיאליים. התוצאה של האינטגרל שכולל את
\( R^{01} \)
כוללת מקדם מספרי
\( c_1 \)
. התוצאה של האינטגרל שכולל את
\( R^{02} \)
כוללת מקדם מספרי
\( c_2 \)
.
יש לבטא את התשובות באמצעות מקדמים אלו (ללא הצבה מספרית). על מנת לקבל את
מלוא הנקודות הביטוי צריך להיות נכון גם מבחינת המקדמים המספריים הנוספים
שמופיעים בחישוב. את התשובות לסעיפים 5-6 אפשר לקבל בדרך פשוטה מאוד ללא
צורך בחישובים מיגעים.
exercise
(6220) אפקט שטארק במערכת של שני אורביטלים
אפקט שטארק מתייחס להשפעה שיש לשדה חשמלי הומוגני על הספקטרום של של אטום או מולקולה.
בגרסא הפשוטה ביותר אפשר לדון באפקט שטארק עבור מערכת "חד מימדית" שכוללת
אלקטרון חסר ספין, בעל מטען
\( q \)
במערכת שכוללת שני אתרים.
האתרים הם מצבים מרחביים המסומנים "1" ו-"2" שהמרחק ביניהם הוא
\( a \).
יתכן שלשני המצבים אין אותה אנרגית קשר (לדוגמה, במקרה של מולקולה שמורכבת משני אטומים שונים).
הניחו שהפרש אנרגיה זה הוא
\( \epsilon \).
בין האתרים יש תדירות קפיצה
\( -\Delta/2 \).
המצבים העצמיים של המערכת הבלתי מופרעת הם מצבים אורביטלים המסומנים בסימון
\( \pm \).
מוסיפים שדה חשמלי חלש
\( f \)
שאליו ניתן להתייחס בתור הפרעה.
עבור האנרגיה של מצב היסוד אפשר לרשום ביטוי מהצורה
\( E(f) = E_0 - \mu f - (1/2)\alpha f^2 + ... \).
המקדמים של האיברים מסדר ראשון ושני נקראים מומנט דיפול, ומקדם הפולריזציה.
(1) הגדירו אופרטור מקום שהערכים העצמיים שלו הם
\( x = \pm (a/2) \).
רישמו את ההמילטוניאן של המערכת כמטריצה 2x2 בצורה
\( H = H_0 + V \).
רישמו ביטויים מפורשים עבור ההמילטוניאן הבלתי-מופרע ועבור ההפרעה, גם בבסיס המרחבי וגם בבסיס האורביטלי.
בנוסף הגדירו, על סמך ההמילטוניאן, את אופרטור הפולריזציה
\( P \).
(2) מיצאו ביטויים מפורשים עבור מומנט הדיפול ועבור מקדם הפולרציזציה על בסיס לכסון מדויק של ההמילטוניאן.
נא להתייחס בניפרד למקרים המיוחדים הבאים:
מולקולה דיפולית
\( \epsilon \ne 0, \Delta = 0 \),
מולקולת האמוניה או אטום המימן ברמת היסוד
\( \epsilon = 0, \ \ \Delta \ne 0 \),
ואטום המימן ברמה המעוררת הראשונה
\( \epsilon = \Delta = 0 \).
ההצדקה להנחות אלו -- ראו סעיף (6).
(3) עבור המקרה שמייצג את "אטום המימן במצב היסוד", קבלו את מקדם הפולריזציה על ידי חישוב תיקון לאנרגיה באמצעות תורת הפרעות סדר שני. ודאו שמתקבלת אותה תוצאה.
(4) עבור המקרה שמייצג את "אטום המימן במצב היסוד", קבלו את מקדם הפולריזציה עלי ידי חישוב ערך התוחלת
\( \langle P \rangle \).
באמצעות תורת הפרעות סדר ראשון עבור מצב היסוד. ודאו שמתקבלת אותה תוצאה.
(5) ודאו שאתם מבינים את ההערה הבאה: עוצמת השדה החשמלי יכולה להיות שונה במקומות שונים במרחב. לכן האטום ירגיש פוטנציאל אפקטיבי
\( U(R) = -(1/2) \alpha |f(R)|^2 \).
פוטנציאל זה מביא לכדי ביטוי את הירידה באנרגיה שנגרמת כתוצאה מהפולריזציה של האטום בתוך השדה החשמלי.
על אובזבציה זו מבוססת השיטה המקובלת ללכידת אטומים באמצעות פוטנציאל אופטי.
(6) הסבירו את ההצדקה להנחות בסעיף (2).
במקרה של אטום המימן העזרו בשאלה 6210 על מנת לרשום המילטוניאן 2x2 שמייצג את האטום בנוכחות שדה חשמלי.
על ידי השוואה לביטוי הפורמאלי של סעיף (1) בצעו זיהוי של מצבי הבסיס
\( \pm \)
ושל הפרמטרים
\( (a, \epsilon, \Delta) \)
המופיעים במודל. שימו לב שנובע מכך שאפשר לפרש את מצבי הבסיס המרחבי, כמצבים שבהם האלקטרון יכול להיות או בצד אחד או בצד מנוגד של הפרוטון.
עבור "אטום המימן במצב היסוד", ועבור אטומים גנריים, הסבירו איזו סימטריה אחראית לכך שלמערכת הבלתי מופרעת יש מומנט דיפול אפס.
עבור "אטום המימן במצב מעורר", הסבירו מדוע ניתן להתייחס אליו מבחינה פורמלית כאל מולקולה דו-אטומית בעלת מומנט דיפול שונה מאפס.
מדוע במקרה האחרון הנימוק הכללי שמסתמך על שיקולי סימטריה לא עובד?
exercise
(6511) מציאת רמות אנרגיה בקרוב סמיקלאסי
2015A
נתון חלקיק בעל מסה
\( M \)
שחופשי לנוע במימד אחד.
מצא בקרוב WKB את רמות האנרגיה
\( E_n \)
של החלקיק במקרים הבאים:
(1) הפוטנציאל הוא
\( V(x)=C|x|^{\alpha} \)
באשר
\( \alpha>0 \)
.
(2) בור פוטנציאל באינטרוול
\( [-a,a] \)
עם רצפת
פוטנציאל
\( V(x)=V_0\text{sign}(x) \)
(3) שאלת בונוס: בסעיף (2) חשב את האנרגיות באמצעות סדר שני בתורת
הפרעות
בסעיף הראשון השתמש בסימון הבא:
\( B(\alpha)=\int_0^1 \sqrt{1-x^{\alpha}} \ dx \)
בסעיף השני מספיק לרשום את התשובה עבור רמות האנרגיה מעל
\( V_0 \)
דינמיקה קוונטית
exercise
(7014) טלפורטציה קוונטית
לאליס יש קיוביט C שהוכן במצב בלתי ידוע
\( |\psi\rangle = \alpha |0 \rangle + \beta |1\rangle \)
כמו כן אליס ובוב חולקים קיוביטים שזורים A ו-B
\( |\Phi_{AB} \rangle = \frac{1}{\sqrt{2}} \left ( |0_A,0_B \rangle + |1_A,1_B \rangle \right) \)
המטרה של פרוטוקול טלפורטציה היא לשעתק את המצב של קיוביט C שנמצא אצל אליס, לקיוביט B שנמצא אצל בוב. הפרוטוקול כולל 3 שלבים. בשלב הראשון אליס שוזרת את המצב של A עם המצב של C. בשלב שני היא מבצעת מדידה של C ושל A, ושולחת את התוצאה אל בוב. בשלב שלישי בוב מבצע
פעולה על B בהתאם לאינפורציה שהוא קיבל על המדידה של אליס.
-
שרטטו תרשים של מעגל שכולל פעולת Hadamard ופעולת CNOT במטרה להכין את המצב השזור \( |\Phi_{AB} \rangle \).
- רישמו את מצב המערכת \( |\psi_C\rangle \otimes |\Phi_{AB}\rangle \) בבסיס הסטנדרטי \( |q_C, q_A, q_B \rangle \)
- הפעילו את האופרטור CNOT על קיוביט A באשר C הוא הקונטרול.
- הפעילו את טרנספורמצית הדמרד על קיוביט C.
- רישמו את 4 המצבים שבוב אמור לקבל בהתאם לתוצאות המדידה של הקיוביטים C ו-A.
- עבור 4 המצבים שרשמתם בסעיף הקודם מצאו מה הם השערים שבהם בוב צריך להשתמש בכדי לקבל את קיוביט B במצב \( |\psi\rangle \).
exercise
(7041) מיחשוב קוונטי של דינמיקת אתרים
נתונה מערכת של 4 אתרים. להלן נניח גאומטרית שרשרת, אבל נתייחס גם לגאומטריית טבעת (תנאי שפה מחזוריים).
מצבי הבסיס מיוצגים באמצעות רגיסטר של שני קיוביטים בצורה הבאה: 00=0, 01=1, 10=2, 11=3.
שרטט סכמת שערים עבור הפעולות הבאות:
(1) החלפת מקום החלקיק בין אתר 2 לבין אתר 3.
(2) פעולת הזזה של החלקיק (הנח גאומטרית טבעת).
(3) אבולוציה - תנועת ההחלקיק מיוצרת על ידי
\( H^A = | 1 \rangle \langle 0 | + | 3 \rangle \langle 2 | + CC \)
(4) אבולוציה - תנועת החלקיק מיוצרת על ידי
\( H^B = | 3 \rangle \langle 1 | + CC \)
(5) אבולוציה - תנועת החלקיק מיוצרת על ידי
\( H^C = | 2 \rangle \langle 1 | + CC \)
(6) אבולוציה על שרשרת. הניחו פרק זמן קצר מאוד (טרוטר).
(7) אבולוציה על טבעת. הניחו פרק זמן קצר מאוד (טרוטר).
(8) אבולוציה על טבעת. פרק זמן שרירותי, ללא קרוב. על בסיס מיספור שונה של האתרים.
טיפ: התשובות לסעיפים 5-7 מתקבלות מיידית מהרכבה של תשובות לסעיפים קודמים: טרנספורמצית דימיון עם הפעולות שהוגדרו בסעיפים 1-2 יכולה לשמש לצורך יצירת הקפיצות הנוספות שאינן כלולות בסעיף (3). ההכללה של (7) לטבעת עם \( 2^N \) אתרים היא מיידית. מצד שני טבעת של 4 אתרים (ריבוע) היא ספרבילית: אפשר למספר את האתרים בצורה שונה, ואז הדינמיקה מיוצגת על ידי שני קיוביטים לא מצומדים. זה מוביל לפתרון הטריוויאלי שאותו אתם מתבקשים להציג בסעיף (8).
exercise
(7045) Supervised evolution in a 2 site system
Consider a particle in a 2 site system. The particle is prepared at \( x=0 \). The subsequent dynamics is generated by \( H =c \sigma_1 \).
A detector is used in order to measure the state of the system.
The result of a statistical measurement provides the probabilities \( p_0 \) and \( p_1 \) to find the particle at \(x=0,1\).
The evolution is commonly described by the function \( F(t)=p_0 \) or by \( M(t)=p_0-p_1 \).
In a supervised evolution, the time is divided into intervals of length \( \tau \).
A measurement is performed at the end of each interval.
Here we assume that the detector supervises the target site \( (x=1) \).
We associate with it a projector \( P=|1\rangle\langle 1| \).
Formally a measurement operation is represented by the formula \(\rho := (1{-}P) \rho (1{-}P) \),
or by the formula \(\rho := P \rho P + (1{-}P) \rho (1{-}P) \),
depending on whether the particle is annihilated or not by the detector.
Accordingly we distinguish between repeated detection scenario and repeated measurement scenario.
In the latter case the \(P \rho P\) term assumes that the detected
particle is re-injected into the target site.
Otherwise, without this term, \( F(t)=\text{Tr}(\rho) \)
is the survival probability in the initial site.
Note:
The questions below can be addressed without reference to the "probability matrix",
using the common phrasing "collapse" for describing the effect of detection.
In a repeated detection scenario, each detection is a projection that describes "collapse" of the wavefucntion.
The norm \( F(t) \) of the remaining wavefunction in such scenario is the probability that the particle survives in the system.
Plotting this norm as a function of time provides the inverse cumulative distribution of the time-to-detection.
(1) Given \( c \), write what are \( F(t) \) and \( M(t) \) for coherent evolution.
(2) Given \( c \) and \( \tau \),
write what is \( F(t) \) for a repeated detection scheme
that consist of \( t/\tau \) (integer) steps.
Assume that the particle is annihilated once detected.
Explain why in this scenario \( F(t) \) decays exponentially.
(3) Given \( c \) and \( \tau \), write what are \( M(t) \) and \( F(t) \)
for a repeated measurement scheme
that consist of \( t/\tau \) (integer) steps.
Assume that the particle is kept in the system.
Describe the evolution using a Bloch picture.
Using this picture explain why in this scenario \( M(t) \) decays exponentially.
(4) Write the results for (2) and (3) in terms of the probability \( p \) to detect the particle at the end of the first interval.
Assume that \( \tau \) is very small the exponential decay can be written as \( \exp(-\Gamma t) \).
Write what is \( \Gamma \) in both cases. Exploit the smallness of \( \tau \) in order to get a simple expression.
For \( \tau \rightarrow 0 \) we get \( \Gamma \propto \tau \rightarrow 0 \).
This is known as the Quantum Zeno effect.
It is not widely recognized that the same effect comes out also in the classical analysis...
exercise
(7051) Quantum Simulation - Two sites
Consider a 2 site system that is represented by a qubit, such that "0" is the first site, and "1" is the second site. The dynamics is generated by \( H =c \sigma_x+(\epsilon/2) \sigma_z \). Define \( U ( t ) = e^{ - i H t} \equiv R ( \theta )\), where \( \theta = 2ct \) is the dimensionless time.
This means that if we choose the units of time such that \( c=1/2 \) then \( \theta = t \). This choice of units is used in subsequent exercises.
(A1) For \( \epsilon = 0 \) use the single rotation matrix RX in order to simulate the dynamics. Plot \( P(\theta ) = |\langle 0|RX(\theta )|0\rangle|^2 \) for \( \theta \in [ 0 , T] \) with \( T=3\pi \). The figure should contain the result of the simulation (stars), compared with the analytical result (line).
(A2) Choose \( N \). Define \( \tau = T /N \). Plot \( P(\theta)=|\langle 0|RX(\tau )...RX(\tau )|0\rangle|^2 \). Check what is the largest value of \(N \) that still provides good results.
Use of Barrier is required (the icon is vertical dashed line), else the IBM-compiler will try to combine gates.
(A3) For a chosen \( N \), plot \( P(\theta)=|\langle 0|(RX(\tau )RZ(\tau ))...(RX(\tau )RZ(\tau ))|0\rangle|^2 \). That is the Trotter approximation. The plot should contain the result of the simulation (stars), compared with the analytical result (line). Add a few lines for different values of \(N\).
(A4) Conclude what is the optimal choice of \( N \). It should not be too small, else the Trotter approximation is bad. It should not be too large, else the IBM computer accumulates errors due to decoherence.
In the above simulation we have considered unitary evolution \( \rho := U \rho U \). In the subsequent simulations we consider measurement and detection scenarios where the \( \rho \) of the "system" undergoes a non-unitary operation due to the coupling to an external degree of freedom ("pointer").
exercise
(7052) Quantum Simulation - Repeated Measurement
Consider a 2 state system, represented by a qubit \( q_{sys} \). The system is prepared at \( (x=0) \). The system can flip state coherently. The dynamics is generated by \( H = c \sigma_x \). Without loss of generality the units of time can be chosen such that \( c=1/2 \), hence the time is like angle. A detector is used in order to measure whether the system is at destination state \( (x=1) \). For a repeated measurement scenario we define \( p(t) \) as the probability to find the particle at the monitored site, and accordingly we define the polarization as \( M(t) = 1-2p(t) \). For a repeated detection scenario we define \( f(t) \) as the probability to detect the particle at time \( t \), and \( F(t) \) as the survival probability. Note that \( f(t_n) = F(t_{n{-}1}) - F(t_n) \), meaning that \( F(t) \) is the inverse-cumulative distribution. For the purpose of presentation one might prefer to plot \( M(t) \) instead of \( p(t) \), and \( F(t) \) instead of \( f(t) \).
The measurement device (so called "pointer") is represented by a 2nd qubit \( q_{meas} \).
The CX operation is required for the performance of the measurement.
This is followed by an IBM readout operation.
The outcome is stored in a classical bit \( c_n \), where \( n=1,2,3,...,N \) labels the bit that is used to store the result of the \( n \)-th measurement. In order to allow repeated measurements, a reset operation on the pointer should be performed after the readout operation.
Statistically speaking, after each measurement the state of the system (i.e. the state of the \( q_{sys} \) qubit)
becomes a mixture of \(x=0\) and \(x=1\).
(B0)
An IBM experiment provides the distribution of \( c = (c_1,c_2,...c_N) \).
Note that there are \(2^N\) possible sequences,
and therefore most of the sequences will have zero count.
The output file of IBM documents only sequences with non-zero count.
Explain how to extract \( p(t_n) \) and \( f(t_n) \) from the outcome of an IBM experiment,
and write a routine for that.
(B1) Build a circuit that simulates a repeated measurement experiment.
The simulation consists of \( N \) time steps.
It is enough to consider evolution up to \( T=2\pi \).
Each time step has duration \( \tau = T/N \), which is like small-angle rotation.
For simulation of coherent evolution the measurement is performed only at the last step.
For simulation of supervised evolution the measurement is performed at each step.
(B2) Perform IBM experiment using your circuits.
Select large enough \( N \) to demonstrate the Zeno effect.
Extract \( F(t) \) and \( M(t) \) from the outcome of the experiment.
Repeat the experiment with a simpler circuit where the readout is done directly on the "system"
without using a pointer. (Such shortcut cannot be implemented in ex7053).
(B3) Compare the the results of the experiment with the analytical predictions of ex7045.
In your plots use symbols for the results of the experiment,
and lines for the the theoretical prediction.
Test different values of \( N \).
exercise
(7053) Quantum Simulation - Repeated Detection
Consider a 4 site chain. We choose units such that the hopping frequency is \( c=1/2 \).
We consider the evolution over a fixed time interval, say \( t \in [0,T] \).
The particle is initially localized at one edge of the chain \(x=0\), which we call launch-site.
A detector is positioned at the opposite edge \(x=11=3\), which we call target.
The detector monitors the target site.
The time between successive measurements is \( \tau = T/N \).
Once the particle is detected the rest of the evolution is of no interest.
We would like to get the probability distribution \( f(t) \) of the time-of-detection.
Note that \( f(t) \) is trivially related to the survival probability \( F(t) \).
(C0) Using e.g. Matlab perform calculation of the expected result.
The choice \( T=20\pi \) might be a good for getting interesting results.
Plot several \( F(t) \) lines for different values of \( N \).
Tip: apparently the best presentation procedure is to plot \( N \log(F(t)) \).
Add a dashed line for the probability to detect the particle in a single (not repeated) measurement that is performed at time \( t \).
(C1) Build a circuit block that simulates
the dynamics of a particle in an isolated 4 site chain
during a time interval \( \tau \).
(C2) Build a multi-block circuit that simulates a repeated-measurement experiment.
The state of the particle in the chain is represented by two qubits,
and the measurement device (so called "pointer") is represented by a 3rd qubit.
Tip: a CCX operation is required for the performance of the measurement.
(C3) Perform an IBM experiment, and plot the probability \( f(t) \) to detect the particle at time \( t \).
Note that given \( T \) the number of measurements \( N \) is a free parameter.
Compare the results of the simulation (stars) to the calculation (solid line).
exercise
(7110) הזזה פתאומית של קיר
חלקיק נמצא בבור פוטנציאל
\( 0<x<L \)
במצב היסוד.
לפתע מזיזים את הקיר כך שרוחב הבור הוא
\( -L<x<L \)
.
מצא את ההסתברות
\( P(n) \)
למצוא את החלקיק ברמת אנרגיה
\( n \)
exercise
(7120) מעברים בין רמות בגין הזזת קיר
2010A
נתון חלקיק בעל מסה M בקופסא חד מימדית
\( x\in[0,a] \)
בעלת צלע a.
בזמן
\( t=-\infty \)
מכינים את החלקיק במצב היסוד של הקופסא.
ההזזה של הקיר השמאלי מתוארת על ידי הפונקציה
\( x=-\epsilon(t) \)
.
נתונה המהירות שבה מזיזים את הקיר
\( \dot{\epsilon} = \frac{\epsilon_0}{\sqrt{2\pi}\tau_0} \exp\left[-\frac{1}{2}\left(\frac{t}{\tau_0}\right)^2\right] \)
להלן הנח שההזזה הכוללת היא קטנה כך שאיבר ההפרעה בהמילטוניאן הוא
\( \langle \varphi |V | \psi \rangle = \mp\left(\frac{\epsilon}{2M}\right) \left[ \frac{\partial\varphi}{\partial x}\right]\left[\frac{\partial\psi}{\partial x}\right] \)
באשר הנגזרות מחושבות בנקודה שבה מצוי הקיר ,
והסימן מינוס (פלוס) מתיחס למקרה של הגדלה (הקטנה).
(1) מצא את ההסתברות
\( P(n) \)
בזמן
\( t=\infty \)
למצוא את החלקיק ברמה מעוררת n
עבור ההזזה מאוד מהירה (פתאומית).
(2) מצא את ההסתברות
\( P(n) \)
במסגרת תורת הפרעות סדר ראשון,
עבור הזזה במהירות סופית.
(3) ענה שוב על הסעיף הקודם אם מזיזים את שני הקירות החוצה ביחד,
כך שהמיקום שלהם מתואר על ידי
\( [-\epsilon(t), \,\, a+\epsilon(t)] \)
(4) הגדר שני תנאים שונים שיכולים להבטיח את תוקף החישוב של תורת הפרעות:
או שמזיזים רק קצת (
\( \epsilon_0 \)
קטן), או שמזיזים מספיק לאט (
\( \tau_0 \)
גדול).
(5) רשום את התנאי על
\( \dot{\epsilon} \)
על מנת שהתהליך יהיה אדיאבטי.
ציין האם במקרה שלפננו התחום האידאבטי מוכל בתחום התקפות של תורת הפרעות,
או מתלכד עם אחד התנאים, או מהווה תחום שונה/נוסף בבעיה.
exercise
(7122) מעברים בין רמות בגין הזזת קיר
2017B
נתון חלקיק בעל מסה M בקופסא חד מימדית
\( x\in[0,a] \)
בעלת צלע a.
בזמן
\( t=-\infty \)
מכינים את החלקיק במצב היסוד
\( n=1 \)
של הקופסא.
ההזזה של הקיר השמאלי מתוארת על ידי פונקציה דמוית-מדרגה
\( x=\epsilon(t) \)
.
המהירות שבה מזיזים את הקיר היא
\( \dot{\epsilon} = \frac{\epsilon_0}{\sqrt{2\pi}\tau_0} \exp\left[-\frac{1}{2}\left(\frac{t}{\tau_0}\right)^2\right] \)
מודדים באיזה רמת אנרגיה נמצא החלקיק בזמן
\( t=\infty \)
(1) חשב את איבר ההפרעה
\( \dot{\epsilon}W_{n,1} \)
למעברים בין מצבים אדיאבטיים.
(2) רשום את התנאי לתוקף של הקרוב האדיבטי.
(3) בהנחה שמדובר בהזזה קטנה
\( \epsilon_0 \ll a \)
של הקיר
חשב במסגרת תורת הפרעות סדר ראשון (בבסיס האדיאבטי)
את ההסתברות
\( P(n) \)
למצוא את החלקיק ברמה מעוררת n
משנים את הפרוטוקול כדלהלן:
- תחילה מזיזים את הקיר השמאלי הזזה קטנה
\( \epsilon_0 \ll a \)
.
- בצורה אדיאבטית לחלוטין מרחיקים את הקיר הימני עד לנקודה
\( x=b \)
- ההזזה של הקיר הימני מתוארת על ידי
\( x=a+v_0 t \)
כך שהזמן הכולל של התהליך הוא
\( t_0=(b-a)/v_0 \)
- בסוף מחזירים את הקיר השמאלי אל הראשית,
כך שההזזה של הקיר השמאלי מתוארת על ידי
\( x=\epsilon(t)-\epsilon(t-t_0) \)
.
(4) מצא את ההסתברות
\( P(n) \)
עבור הפרוטוקול החדש.
הדרכה: איבר ההפרעה עבור הזזה אינפיניטסימאלית של הקיר הוא
\( \langle \varphi |V | \psi \rangle = -\left(\frac{\epsilon}{2M}\right) \left[ \frac{\partial\varphi}{\partial x}\right]\left[\frac{\partial\psi}{\partial x}\right] \)
באשר הנגזרות מחושבות בנקודה שבה מצוי הקיר.
הבע את התוצאות באמצעות הנתונים
\( (M, a, b, v_0, \epsilon_0, \tau_0) \)
את התוצאה בסעיף 3 רשום בצורה
\( P(n)=|A(a)|^2 \)
.
את התוצאה בסעיף 4 הבע באמצעות הפונקציה
\( A(\cdot) \)
והנתונים.
exercise
(7212) העברה אדיאבטית לאורך שרשרת
2019A
בבעיה זו אנו מתיחסים לשרשרת עם מספר אי זוגי של אתרים.
לצורך מתן תשובות נניח שמדובר בשרשרת שמורכבת מ-5 אתרים
\( x=1,2,3,4,5 \)
.
תדירויות הקפיצה בין האתרים הן
\( (a,b,a,b) \)
באשר
\( a=c\sin(\theta); \ b=c\cos(\theta) \)
.
האנרגיה הפוטנציאלית בכל האתרים היא אפס, למעט באתר השני שם היא
\( V \)
.
בהתחלה שמים חלקיק באתר הראשון, ואז משנים בהדרגה את פרמטר הבקרה
מהערך
\( \theta=0 \)
לערך
\( \theta=\pi/2 \)
בקצב
\( \dot{\theta} \)
.
(1) עבור
\( V=0 \)
רשום את המטריצה
\( R \)
שמיצגת פעולת כיול כך שמתקיים
\( R^{-1}HR = -H \)
.
מכאן אנו מסיקים שיש להמילטוניאן מצב עצמי עם ערך עצמי
\( E=0 \)
.
(2) עבור
\( V=0 \)
רשום בבסיס הסטנדרטי את המצב האדיאבטי המשתמע מתנאי
ההתחלה.
איפה יהיה החלקיק בסוף תהליך אדיאבטי?
האם התשובה תלויה במחסום הפוטנציאל
\( V \)
?
(3) עבור
\( V=0 \)
רשום את האנרגיות העצמיות עבור
\( \theta=0 \)
ועבור
\( \theta=\pi/4 \)
.
טיפ: שים לב שבמקרה השני הבעיה זהה פורמאלית לבור-פוטנציאל ברוחב
\( L=6 \)
.
(4) כנ"ל אם מתקיים
\( V\gg c \)
.
מספיק leading order (סדר אפס/ראשון/שני בהתאם לנסיבות).
סעיף זה דורש ליכסון של מטריצה 3x3 על מנת לקבוע את אחת האנרגיות.
יש להקפיד על הנכונות של המקדם המספרי בתוצאה.
(5) צייר שרטוט סכמטי של האנרגיות העצמיות כפונקציה של
\( \theta \)
עבור
\( V=0 \)
.
צייר שרטוט סכמטי של האנרגיות העצמיות כפונקציה של
\( V \)
עבור
\( \theta=0 \)
.
יש להקפיד שהציור יהיה ברור ולא מקושקש.
(6) מה התנאי האדיאבטי על
\( \dot{\theta} \)
.
הבחן בין המקרה
\( V=0 \)
והמקרה
\( V\gg c \)
.
פקטורים נומריים לא חשובים.
טיפ: גם בלי לפתור את סעיפים (1-2) עדיין אפשר להתמודד בהצלחה עם שאר
הסעיפים.
תורת הפרעות לאבולוציה בזמן (אלמנטרי)
exercise
(7320) חלקיק בבור פוטנציאל + פולס דלתה
2007A3
נתון בור פוטנציאל ברוחב
\( -(L/2)<x<(L/2) \)
עם תנאי שפה אפס בקצוות.
בזמן
\( t=-\infty \)
מכינים חלקיק בעל מסה
\( m \)
בתוך הבור במצב היסוד (
\( n=1 \)
).
(א) רשום את פונקצית הגל של החלקיק.
מדליקים הפרעה
\( V(x)=-\mathcal{E} e^{-\frac{1}{2}(t/\tau)^2} \delta(x) \)
, באשר
\( 0<\mathcal{E} \)
(ב) חשב את ההסתברות
\( P(n) \)
למצוא את החלקיק בסוף התהליך (
\( t=\infty \)
)
ברמות האנרגיה
\( n=2,3,4,... \)
.
הערה:
\( FT[e^{-\frac{1}{2}(t/\tau)^2}]=\sqrt{2\pi}\tau e^{-\frac{1}{2}(\tau\omega)^2} \)
בסעיפים הבאים הנח ש-
\( \mathcal{E} \)
הוא מאוד גדול, אבל מאידך התהליך הוא אדיאבטי .
(ג) רשום את פונקצית הגל של החלקיק בזמן
\( t=0 \)
.
(ד) רשום את התנאי לכך שהקרוב האדיאבטי תקף.
exercise
(7380) דינמיקה במערכת שני אתרים עם הינע חיצוני
מערכת יכולה להיות ב 2 מצבים ללא הסתברות מעבר ביניהם.
הפרש האנרגיה בין המצבים האלו הוא
\( \varepsilon \).
מוסיפים הפרעה תלויה בזמן שמצמדת את שני המצבים:
\( V=\left( \array{ 0 & \gamma e^{i \Omega t} \\ \gamma e^{-i \Omega t} & 0 } \right) \)
שימו לב שקיימת אנלוגיה פורמאלית לבעיה של ספין חצי בשדה מגנטי,
כך שניתן לרשום את ההמילטוניאן בצורה
\( H = \vec{h}(t) \cdot \vec{S} \).
בזמן
\( t=0 \)
המערכת נמצאת במצב היסוד.
-
מצא\י את ההסתברות להיות במצב היסוד ובמצב השני, בסדר ראשון בתורת הפרעות.
-
מצא\י את ההסתברות להיות במצב היסוד ובמצב השני באופן מדויק.
-
מצא\י דרך מיידית לקבל את התוצאה המדויקת על ידי מעבר למערכת "מסתובבת", וניצול של נוסחת רבי.
כלל הזהב של פרמי
exercise
(7680) דעיכת גאמוב מתוך טבעת
2011B
חלקיק בעל מסה
\( M \)
כלוא בתוך התקן חד מימדי שאורכו
\( L_0 \)
.
אל ההתקן החד מימדי ניתן להתיחס כאל "בור פוטנציאל"
\( (0<x<L_0) \)
עם תנאי שפה אפס בקצוות.
מכינים את החלקיק באחת מרמות האנרגיה
\( E_n \)
באשר
\( n=1,2,3,4... \)
.
מהירות החלקיק בתוך הבור מוגדרת באמצעות הביטוי
\( v_n=(2E_n/M)^{1/2} \)
.
החלקיק יכול לברוח אל מצבי
\( k \)
של מוליך חד מימדי ארוך מאוד.
אופן הצימוד של ההתקן אל המוליך מתואר בשרטוט.
אל נקודת החיבור נתייחס כאל "מחסום דלתא"
\( V(r)=u\delta(r) \)
.
אלמנטי המטריצה של הצומת הם
\( V_{nk} = -\frac{1}{4M^2 u} [\partial \psi^{(n)}] [\partial \psi^{(k)}] \)
,
באשר
\( \partial \)
היא הניגזרת בכיוון הרדיאלי (הקואורדינטה
\( r \)
מכוונת מהצומת כלפי חוץ).
מקדמי המעבר (
transmission
) של נקודת החיבור הם
\( g_1, g_2 \ll 1 \)
.
להלן יש להביע את כל התשובות באמצעות
\( (L_0, M, v_n, g_1,g_2) \)
.
(1) שאלה מקדימה: רשום מה הן רמות האנרגיה
\( E_n \)
ופונקציות הגל העצמיות
\( \psi^{(n)}(x) \)
.
(2) רשום ביטוי מפורש עבור אלמנטי המטריצה
\( V_{nk} \)
בין מצבי ההתקן לבין מצבי המוליך.
(3) רשום ביטוי מפורש עבור צפיפות מצבי האנרגיה
\( (dN/dE) \)
בתוך המוליך הארוך.
(4) מצא את קבוע הדעיכה
\( \Gamma_n \)
של כל אחד מהמצבים.
(5) הכלל את הנוסחא למקרה שבו יש שטף מגנטי
\( \Phi \)
דרך הטבעת. הנח שמטען החלקיק הוא e.
הדרכה + רמזים:
בסעיף (2) הנח
\( g_2=0 \)
. בנוסף הנח
\( E_k \approx E_n = (1/2)Mv_n^2 \)
.
בשלבי הביניים ניתן להניח שאורך המוליך הארוך הוא
\( L \)
(סופי),
אך בתשובה הסופית של סעיף (4) נתון זה אמור "להצטמצם".
הנוסחא לעבירות של מחסום דלתא גדול מאוד היא
\( g \approx (v_n/u)^2 \)
.
סעיף (5) לא דורש עבודה אלגברית נוספת אלא הבנה פיסיקלית בלבד.
exercise
(7684) חלקיק באתר שמצומד לטבעת גדולה
2013A
חלקיק בעל מסה
\( M \)
כלוא בתוך אתר. אנרגית הקשר הבלתי מופרעת היא
\( \varepsilon_0 \)
.
האתר מצומד לטבעת גדולה באורך
\( L \)
בנקודה אחת, כך שמתקיים
\( \langle \varepsilon_0 | H | \psi \rangle = \alpha \psi(x_0) \)
בסעיף 1 הנח שהאנרגיה
\( \varepsilon_0 \)
היא מתחת לרצפת הפוטנציאל של הטבעת.
-
חשב את התיקון
\( \Delta \)
לאנרגית הקשר, על ידי שימוש בתורת
הפרעות סדר שני.
-
כנ"ל בהנחה שהאנרגיה
\( \varepsilon_0 \)
היא מעל לרצפת הפוטנציאל של הטבעת.
-
במקרה האחרון - חשב את קבוע הדעיכה
\( \Gamma \)
של המצב הקשור.
-
מצא את תחום ערכי
\( \varepsilon_0 \)
שבו לא ניתן לבטוח בתוצאות שקיבלת בסעיפים
הקודמים.
-
את אנרגית הקשר בסעיף 1 אפשר למצוא במדויק, על ידי פתרון של משוואה
ממעלה שלישית. רשום את המשוואה.
הדרכה:
-
נוח לעבוד בבסיס התנע
\( |k\rangle \)
של הטבעת
-
הנח שהטבעת גדולה מאוד כך שניתן לקרב את הסכום באמצעות אינטגרל.
-
בסעיף (3) השתמש בכלל הזהב של פרמי.
-
הבע את התשובות הסופיות באמצעות
\( \alpha, M, \varepsilon_0 \)
-
אם זה מפשט את הביטוי, מותר ומומלץ להשתמש בסימון
\( v_0 = (2\varepsilon_0/M)^{1/2} \)
קרוב בורן לחתך הפעולה
exercise
(7850) חישוב חתך פעולה עבור פוטנציאל גאוסי
מצא את חתך הפעולה הדיפרנציאלי ואת חתך הפעולה הכולל בקרוב בורן
עבור פוטנציל גאוסי
\( U(r)=U_0 e^{-(r/a)^2/2} \)
.
הגדר\י את התנאים לכך שקרוב בורן יהיה תקף.
exercise
(7860) חישוב חתך פעולה עבור פוטנציאל יוקאווה (רתרפורד מקרה פרטי)
מצא את חתך הפעולה הדיפרנציאלי ואת חתך הפעולה הכולל בקרוב בורן
עבור פוטנציאל יוקאווה
\( U(r)=U_0 \frac{e^{-r/a}}{r} \)
.
הגדר\י את התנאים לכך שקרוב בורן יהיה תקף.
שים לב שפיזור רתרפורד הוא גבול מיוחד של יוקווה.
The propagator and the Green function
Formal perturbation theory
Scattering theory
Scattering [1D]
Scattering [3D]
Scattering [3D, Born]
Quantum fields
Many body systems
Interaction with the EM field