קוסמולוגיה
Friedmann equations - Wiki
Cosmic dynamics - lecture notes
פתרון מעניין נוסף של משוואות איינשטין מתייחס לטנסור המטרי של היקום כולו. נניח שהיקום מלא במסה בצפיפות אחידה. נחפש פתרון שמתואר על ידי הטנסור המטרי של רוברסטון-וולקר. הנעלמים הם העקמומיות של המרחב K והתלות בזמן של פקטור הסקאלה
\(\displaystyle{ a(t) }\)
. נדגיש מראש שתצפיות אסטרונומיות מאפשרות "למדוד" את גדלים אלה. מתוך משוואות אינשטיין נקבל את משוואות פרידמן:
\(\displaystyle{ 3\frac{\dot{a}^2 + K}{a^2} \ \ = \ \ 8\pi\rho }\)
\(\displaystyle{ \frac{2\ddot{a} a + \dot{a}^2 + K}{a^2} \ \ = \ \ -8\pi p }\)
מכאן מקבלים משוואות עבור הקצב והתאוצה של התפשטות היקום:
\(\displaystyle{ \frac{\dot{a}^2 +K}{a^2} \ \ = \ \ \frac{8 \pi}{3}\rho }\)
\(\displaystyle{ \frac{\ddot{a}}{a} \ \ = \ \ -\frac{8 \pi}{6}\left(\rho+3p\right) }\)
המשוואה הראשונה קושרת בין צפיפות האנרגיה ביקום לבין קצב ההתפשטות שלו. המשוואה השניה קובעת את הקצב שבו ההתפשטות מואטת או מואצת. אם גוזרים את המשוואה הראשונה ומחסירים אותה מהמשוואה השניה מקבלים נוסחא עבור הקצב שבו משתנה צפיפות האנרגיה ביקום:
\(\displaystyle{ \dot{\rho} \ \ = \ \ -3\frac{\dot{a}}{a}(\rho+p) }\)
להלן נגדיר את הנפח, המסה, והאנרגיה של היקום בצורה הבאה:
\(\displaystyle{ V=\frac{4\pi}{3}a^3, \ \ \ \ E=M=V\rho }\)
את המשוואה הראשונה של פרידמן אפשר לרשום בצורה שמזכירה את חוקי הדינמיקה הניוטונית:
\(\displaystyle{ \frac{1}{2}M \dot{a}^2 \ - \ \frac{M^2}{a} \ = \ const }\)
את קצב שינוי צפיפות האנרגיה אפשר לבטא באמצעות קצב שינוי המימדים של היקום. כאשר היקום מתפשט הלחץ עושה "עבודה" ולכן האנרגיה של היקום קטנה
\(\displaystyle{ dE = -pdV }\)
. זה מוביל לקשר
\(\displaystyle{ d\rho= -(\rho+p)\frac{dV}{V} }\)
ומכאן מתקבלת המשוואה עבור
\(\displaystyle{ \dot{\rho} }\)
.
הקבוע הקוסמולוגי
לקבוע הקוסמולוגי של אינשטיין אפשר לפרש כאנרגיה "אפלה" בעלת צפיפות
\(\displaystyle{ \rho = \Lambda / (8\pi) }\)
שממלאת את הואקום. לפי האינטרפטציה המקובלת זה משקף פלקטואציות קוונטיות של הואקום. אם מגדילים את הנפח של היקום האנרגיה האפלה שלו גדלה בהתאם
\(\displaystyle{ dE = +[\Lambda/(8\pi)] dV }\)
. זה אומר שיש לייחס לאנרגיה האפלה לחץ שלילי
\(\displaystyle{ p = -\Lambda / (8\pi) }\)
. לחץ שנובע מפלקטואציות של הואקום נקרא "אפקט קזימיר". אנו נרחיב לגבי אפקט קזימיר בהמשך, תוך התיחסות לאספקט אחר (מספר המימדים של היקום). נרשום את מישוואות פרידמן תוך אבחנה בין צפיפות "החומר" לבין "האנרגיה האפלה"
\(\displaystyle{ \frac{\dot{a}^2 +K}{a^2} \ \ = \ \ \frac{8 \pi}{3}\rho_M \ + \ \frac{1}{3} \Lambda }\)
\(\displaystyle{ \frac{\ddot{a}}{a} \ \ = \ \ -\frac{8 \pi}{6}\left(\rho_M+3p_M\right) \ + \ \frac{1}{3} \Lambda }\)
נשים לב שחומר "רגיל" מאיט את קצב ההתפשטות של היקום, בעוד שאנרגיה אפלה מאיצה את קצב ההתפשטות של היקום. במקור אינשטיין הציע להוסיף את הקבוע הקוסמולוגי למשוואה שלו, כיוון שהוא האמין שהיקום אמור להיות סטאטי. בהמשך, כאשר האבל גילה שהיקום מתפשט אינשטטין תיאר את הרעיון שלו במילים
"the biggest blunder of his life"
. אבל כיום מהתצפיות האסטרונומיות נובע שיש להניח שהאנגיה האפלה היא למעשה 70% מהאנרגיה ביקום.
הפרמטר של האבל
בטנסור של רוברסטון-וולקר יש שני גדלים שניתן לקבוע אותם על סמך תצפיות אסטרונומיות: העקמומיות ופקטור הסקאלה. מדידות של קרינת הרקע הקוסמית מעידות על כך שעקמומיות המרחב היא קרובה לאפס. את התפשטות היקום מתארים באמצעות הפרמטר של האבל:
\(\displaystyle{ H \ \ = \ \ \text{Hubble parameter} \ \ \equiv \ \ { \frac{\dot{a}}{a}} }\)
מבחינה תצפיתית פרמטר זה קובע את היחס בין מהירות ההתרחקות לבין המרחק של שתי גלאקסיות (לגלאקסיות רחוקות יש מהירות התרחקות גבוהה יותר). על ידי הצבת הערך הנמדד של H במשוואה הראשונה של פרידמן, אפשר לקבל מה אמורה להיות צפיפות האנרגיה ביקום. בנוסף, מהמדידות האסטרונומיות של H עבור גלאקסיות רחוקות, אפשר להסיק שקצב ההתפשטות של היקום מואץ. זה מוביל, על סמך המשוואה השניה של פרידמן, למסקנה שכ-70% מהאנרגיה ביקום היא למעשה "אנרגיה אפלה". השאר זה "חומר", שבחלקו הגדול לא ניתן לראות באמצעות טלסקופים, אבל האופן שבו מאורגנות הגלאקסיות מעידות על קיומו.
סקאלת האורך של פלאנק
עד עכשיו תארנו את הגרביטציה במסגרת של הפיסיקה הקלאסית. נשאלת השאלה מה סקאלת האורך שבה לא ניתן להתעלם מאפקטים קוונטיים. את סקאלה זו ניתן לקבוע באמצעות השיקול הבא. נניח שאנו מודדים את הזמן ביחידות סטנדרטיות seconds. את האורך אנו גם מודדים ב-seconds כך שמהירות האור שווה לאחד, ומכאן שיחידות המסה במסגרת המכניקה הקוונטית הן
1/second
(במילים אחרות גם קבוע פלאנק שווה לאחד). במערכת זו של יחידות פיסיקליות קבוע הגרביטציה הוא
\(\displaystyle{ G \ \ = \ \ \frac{\hbar}{c^5}G_{\text{standard units}} \ \ = \ \ \left(5.4\cdot 10^{-44} \ sec\right)^2 }\)
אנחנו רואים שקבוע הגרביטציה מגדיר סקאלת אורך "טבעית" שנקראת סקאלת האורך של פלאנק. על מנת להבין את המשמעות של הסקלה הזו נדמיין שאנחנו כולאים פוטון באזור מרחבי שהרדיוס שלו R. המאסה הגרביטציונית של הפוטון שווה לאנרגיה שלו, אשר נקבעת לפי אורך הגל שלו:
\(\displaystyle{ M \ \ = \ \ E \ \ = \ \ \omega \ \ = \ \ \mid k\mid \ \ \sim \ \ \frac{1}{R} }\)
על מנת שיהיה אפשר "לראות" את הפוטון, רדיוס שוורצילד שלו צריך להיות קטן יותר מהרדיוס שבו הוא כלוא. אחרת הוא הופך להיות חור שחור. אוביקט הופך להיות "חור שחור" אם הרדיוס שלו קטן מרדיוס-שווארשילד שנקבע על ידי המסה שלו:
\(\displaystyle{ R \ \ \ < \ \ \ r_s = 2G M }\)
מכאן מקבלים שהפוטון הממוקם יהפוך להיות "בלתי נראה" אם אורך הגל שלו
\(\displaystyle{ R \ \ \ < \ \ \ \sqrt{G}\equiv \text{Plank Length} }\)
אגב, המסה של פלאנק היא בערך כמו המסה של גרגיר חול
\(\displaystyle{ \text{Plank Mass} \ \ = \ \ \frac{1}{\text{Planck Length}} \ \ = \ \ 2.2 \cdot 10^{-8} \ kg }\)
אפקט קזימיר
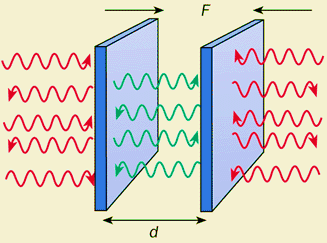
האפקט הזה מתייחס לכוח המשיכה שקיים בין שני לוחות בגין הקוונטיזציה של המודים האלקטרומגנטיים (ראה ציור). זה אנלוגי לכוח המשיכה בין שתי אוניות בגלל גלים עומדים שנוצרים ביניהם. נתבסס על הנוסחא של אנרגית אוסצילטור:
\(\displaystyle{ E^{(n)}_{\nu} \ \ = \ \ \left(\frac{1}{2}+\nu\right) \hbar\omega_n, \ \ \ \ \ \ \nu=0=\text{vacuum} }\)
נסכם את אנרגית הואקום של כל המודים
\(\displaystyle{ \omega_n \ \ = \ \ n\omega_{\perp} \ \ = \ \ n\frac{\pi}{d} }\)
נקבל שהאנרגיה הכוללת של מצב היסוד היא שלילית (לכן הלוחות מושכים זה את זה).
החישוב מוצג להלן. נשים לב שאנרגית היחוס היא במצב שבו הלוחות במרחק אינסופי אחד מהשני.
\(\displaystyle{ E(\infty) \ \ = \ \ \sum_{n=1}^{\infty} \frac{1}{2} \hbar \left (n \frac{\pi}{L} \right) \ \ = \ \ \frac{L}{\pi}\int_{0}^{\infty} \frac{1}{2} \hbar \omega d\omega }\)
\(\displaystyle{ E(d) \ \ = \ \ \sum_{n=1}^{\infty} \frac{1}{2} \hbar \left (n \frac{\pi}{d} \right) \ + \ \frac{L-d}{\pi}\int_{0}^{\infty} \frac{1}{2} \hbar \omega d\omega }\)
\(\displaystyle{ E(d) - E(\infty) \ \ = \ \ \frac{1}{2}\left[ \sum_{n=1}^{\infty} n \ - \ \int_{0}^{\infty} n dn \right] \, \hbar\omega_{\perp} \ \ \approx \ \ -\frac{1}{24} \hbar\omega_{\perp} }\)
על מנת לבצע את החישוב מכניסים אקספוננט דועך, מבצעים את הסכום ואת האינטגרל, ומשאיפים את קבוע הדעיכה לאפס.
Wikipedia:
\(\displaystyle{ 1+2+3+4+\cdots=-\frac{1}{12} }\)
כמה מימדים יש למרחב הפיסיקלי?
לכאורה למרחב הפיסיקאלי יש 4 מימדים: מימד אחד של זמן ועוד שלושה מימדים של אורך. שיקול מתמטי ספקולטיבי של "תורת המיתרים" מוביל למסקנה שלמרחב הפיסקלי יש 10 מימדים. ההסבר הפורמאלי של מדוע צריך את תורת המיתרים, ומדוע צריכים 10 מימדים, יאמר להלן, אבל הוא לא מאיר עיניים. לכן בהמשך ננסה להסביר את המשמעות של הטענה על ידי שימוש באנלוגיה לפיסיקה של סיבים אופטיים...
תורת המיתרים:
דיראק הראה שאם רוצים לנסח מכניקה-קוונטית במסגרת "יחסות פרטית" עבור אוביקט
נקודתי
, אז האוביקט הזה חייב להיות בעל ספין, והוא חייב ליצג את האפשרות שהוא יהיה "חלקיק" או "אנטי חלקיק" בהתאם לאופן שבו מעוררים אותו. מתברר אם רוצים לנסח מכניקה-קוונטית במסגרת "יחסות כללית" (הבסיס של אינשטיין לתורת הגרביטציה) אז האוביקט הזה חייב להיות "
מיתר
" בעל אורך סופי (אחרת החישובים "מתפוצצים"). להלן נסמן את אורך המיתר בסימון
\(\displaystyle{ d }\)
, ונניח שהוא מסדר גודל של אורך פלאנק. מתברר שעל מנת לשמור על עקרונות היחסות עבור "מיתר", המרחב חייב להיות בעל מספר מסוים של מימדים (ראה פרוט נוסף בהמשך). הספקולציה היא שהחלקיקים שאנו מוצאים במודל-הסטדנרטי הם עירורים שונים של אותו אוביקט מתמטי: זה אומר שאם יוצרים/מעוררים מיתר בצורה אחת מקבלים "פוטון", ואם יוצרים/מעוררים מיתר בצורה אחרת מקבלים "אלקטרון".
מימדים נוספים:
נניח שאנו מסתכלים על האוקיאנוס ממרחק גדול. מה שאנו רואים זה משטח דו מימדי שעל פניו נעים אוביקטים שלהם אנו קוראים "גלים". אם מסתכלים יותר מקרוב מבינים שהגלים הם למעשה אכסיטציות שקימות בגלל שיש מימד שלישי (אנכי). אפשר להגיד שמבחינה מתמטית האוקיאנוס הוא יריעה תלת מימדית עם שני מימדים "רחבים" ומימד אחד "דק". באנלוגיה אנו יכולים לשער שאולי "הפוטונים" שקימים במרחב הפיסיקלי הם למעשה אכסיטציות של מימד נוסף שיש למרחב. באופן כללי יותר אפשר לשער שכל "החומר" שמופיע במודל הסטנדרטי נובע מאכסיטציות של מימדים נוספים "דקים". במבט ראשון אפשר לחשוב שמספר המימדים הנוספים של המרחב הפיסיקאלי צריך לשקף את מספר השדות שיש במודל הסטדנדרטי: שדות בוזוניים (פוטונים, גלואונים) ושדות פרמיוניים (קוארקים ולפטונים). אבל המכניקה הקוונטית מראה שבתאוריה קונסיסטנטית מספר המימדים של המרחב הפיסקאלי חייב להיות 10. אם היו במודל הסטנדרטי רק בוזונים מספר המימדים של המרחב הפיסקאלי היה חייב להיות 26. את המספר הזה נסביר להלן.
מסה של פוטון:
כדי ליצור חלקיק במרחב דרושה אנרגיה. האנרגיה הזו מורכבת ממסת המנוחה פלוס אנרגיה קינטית. להלן נסביר שמסת המנוחה של הפוטון במסגרת תורת-המיתרים היא
\(\displaystyle{ m \ \ = \ \ \left\{ 1 \text{[quanta]} \ \ - \ \ \frac{D}{24} \text{[casimir]} \right\} \ \hbar\omega_{\perp} }\)
ונדרוש שהיא תהיה אפס. הדרישה
\(\displaystyle{ m=0 }\)
מובילה למסקנה שלמרחב צריכים להיות 26 מימדים: מימד אחד של זמן, מימד אחד של אורך בכיוון תנועת הפוטון, ועוד
\(\displaystyle{ D=24 }\)
מימדים נוספים. לצורך ההסבר של הנוסחא נשים לב שאותו אפקט קיים בסיבים אופטיים. עירור של תנודה אלקטרומגנטית בעלת תנע
\(\displaystyle{ k }\)
בסיב אופטי בעל עובי
\(\displaystyle{ d }\)
כרוך בתשלום מינימלי
\(\displaystyle{ \omega_{\perp}=\pi/d }\)
שנובע מקיומה של דרגת החופש הטרנסורסלית. את התשלום הזה אפשר לפרש כמסת מנוחה של הפוטון שנע לאורך הסיב:
\(\displaystyle{ \epsilon \ \ = \ \ \mid \vec{k}\mid \ \ = \ \ \sqrt{\left(\frac{\pi}{d} \right)^2 + \left(k_{\parallel}\right)^2 } \ \ \equiv \ \ \sqrt{m^2+p^2} }\)
זה מסביר את האיבר הראשון בנוסחא של תורת המיתרים. נסביר עכישו את האיבר השני. במסגרת תורת-המיתרים הפוטון הוא מיתר שעוררו אותו. מהמחיר
\(\displaystyle{ \hbar\omega_{\perp} }\)
של יצירת הערור יש להחסיר את הרווח האנרגטי שכרוך ביצירת המיתר. כאשר יוצרים מיתר בעל אורך
\(\displaystyle{ d }\)
באזור מרחבי מסוים, זה כמו ליצור גאומטרית קזימיר בכיוון הטרנסורסלי (בכיוון המאונך לכיוון תנועתו). את התוצאה שמצאנו באנליזה של אפקט קזימיר יש להכפיל במספר המימדים הטרנסורסלים
\(\displaystyle{ D }\)
. אנו דורשים שהסכום
\(\displaystyle{ m }\)
(המחיר של העירור לאחר הנחה) יהיה שווה לאפס: זה מוביל למסקנה
\(\displaystyle{ D=24 }\)
.
David Tong: Lectures on String Theory [arXiv]
הערה על רנורמליזציה
ההערה להלן חורגת מרמת הקורס ואני רושם אותה לצורך שלמות הסקירה.
כאשר מנסים לחשב חתכי פעולה של פיזורים במסגרת "מודל סטנדרטי" של חלקיקים נקודתיים מופיעים בחישוב אינטגרלים מתבדרים. על מנת למנוע את ההתבדרות יש להכניס cutoff, זה אומר להתיחס לחלקיק כאילו הוא בעל גודל סופי (או לחילופין כאילו למרחב יש רזולוציה סופית). התשובה הסופית לא אמורה להיות תלויה ב-cutoff. הסכמה המתמטית לביצוע החישוב נקראת "רנורמליזציה".
המודל הסטנדרטי הוא "בסדר" מבחינת רנורמליזציה. זה הודות לכך שבמודל "הערום" (ללא אינטראקציות) יש לכל החלקיקים מסה אפס. המסה הסופית של החלקיקים מושגת כאשר מוסיפים את האינטראקציה בגלל "שבירת סימטריה". זה נקרא
מנגנון היגס
. אחד מההשגים החשובים של הפיסיקה הניסיונית בעשור האחרון היה לודא את קיומם של חלקיקי היגס שהם תוצר נלווה של שבירת הסימטריה.
אבל אם מנסים לקחת בחשבון גרביטציה אז יש צרות. תורת הגרביטציה היא "לא בסדר" מבחינת רנורמליזציה. הבעיה קשורה לכך שיש את
סקאלת פלאנק
. כל חישוב שדורש רזולוציה גבוהה יותר מתפוצץ. הפתרון לכך הוא להניח שהחלקיקים האלמנטריים הם לא אוביקטים נקודתיים אלא "מיתרים". הודות לספקולציה זו, הבעיה של הרנורמליזציה הופכת להיות בלתי רלונטית.
מצד שני התאור הקוונטי של מיתר הוא מסובך יותר מהתאור הקוונטי של חלקיק נקודתי. מתברר שעל מנת לשמור על האינורינטיות של התאור הקוונטי תחת טרנספורמצית לורנץ, יש להניח שלחלקיקים של התאוריה יש
מסה אפס
. זה מתקיים רק אם למרחב יש מספר מסוים של מימדים (כפי שהוסבר בסעיף הקודם).
נחזור לעניין הגרביטציה: אם מתייחסים לטנסור המטרי של המרחב כאל שדה, אז העירורים הקוונטיים של השדה הזה הם מבחינה פורמאלית חלקיקים חסרי מסה בעלי ספין2. על פי טיעון של פינמן-ווינברג גם ההפך הוא נכון. אם תאוריה מנבאת את קיומם של עירורים כאלה, הרי משתמע מכך שהיא באופן טבעי מהווה תאוריה של גרביטציה קוונטית. הטענה היא שתורת המיתרים אכן מספקת את הסחורה גם בהיבט זה. במילים אחרות הספקולציה היא שתורת מיתרים (עתידית) תאחד את תורת הגרביטציה עם המודל הסטנדרטי, ותהיה
theory of everything
