מדידה קוונטית, החתול של שרדינגר
forum link
החתול של שרדינגר הוא ניסוי מחשבתי בתורת הקוואנטים. מטרת הניסוי
המחשבתי להוכיח שאם המכניקה הקוונטית תקפה בעולם המיקרוסקופי, אז מן
הסתם היא גם תקפה בעולם המקרוסקופי. במילים אחרות אם אפשר לגרום לאטום
להיות בסופרפוזיציה של שני מצבים, אז אפשר גם לגרום לחתול להיות
בסופרפוזיציה של שני מצבים, ובפרט אפשר ליצור מצב שבו החתול מצוי
בסופרפוזיציה של חיים ומוות. הרעיון הוא "לשעתק" מצב סופרפוזיציה של
אטום.
מהלך הניסוי: כולאים חתול בתוך קופסא הסגורה לעולם מבחוץ. לא ניתן
לצפות במתרחש בתוך הקופסא. בתוך הקופסא יש אטום רדיואקטיבי המשחרר
פוטון בעת ההתפרקות. בנוסף יש בקופסא גלאי, ומנגנון הריגה המחובר
לגלאי. ברגע שהגלאי מגלה התפרקות, הוא מפעיל את מנגנון ההריגה.

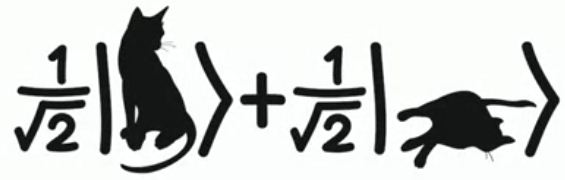 \(\displaystyle{ \Huge
\Psi \ = \ \ }\)
\(\displaystyle{ \Huge
\Psi \ = \ \ }\)
הכנת אטום במצב סופרפוזיציה
-
אטום במצב מעורר:
\(\displaystyle{ | \uparrow\rangle
}\)
-
אטום במצב היסוד:
\(\displaystyle{ | \downarrow\rangle }\)
-
המצב של האטום לאחר "זמן מחצית חיים":
\(\displaystyle{
| \Psi\rangle = | \uparrow\rangle + | \downarrow\rangle
}\)
הערה: כשאטום דועך למצב היסוד הוא משחרר פוטון.
הערה: בהרצאה זו אנו משמיטים פקטורי נירמול כדי לא לסרבל את הכתיבה.
הכנת חתול במצב סופרפוזיציה
האם ניתן להכין גם חתול בסופרפוזיציה?
-
חתול חי:
\(\displaystyle{ | u \rangle }\)
-
חתול מת:
\(\displaystyle{ | d \rangle }\)
-
סופרפוזיציה:
\(\displaystyle{ | \Psi\rangle = | u \rangle + |
d \rangle }\)
מתכון להכנת חתול בסופרפוזיציה של חיים ומוות:
-
השג אטום במצב מעורר
\(\displaystyle{ | \uparrow\rangle }\)
-
ארגן מתקן הרעלה:
אם האטום "דועך" למצב היסוד הוא משחרר פוטון שגורם לשחרור
רעל
-
שים את החתול החי ביחד עם האטום במתקן
\(\displaystyle{ |
\uparrow,u \rangle }\)
-
אם מחכים הרבה זמן המצב שיתקבל יהיה
\(\displaystyle{ | \downarrow,d
\rangle }\)
-
אם מחכים "זמן מחצית חיים" המצב שמתקבל הוא:
\(\displaystyle{ | \Psi\rangle =
| \uparrow,u \rangle + | \downarrow,d \rangle }\)
הערה:
למעשה זה לא החתול אלא כל המערכת שנמצאת בסופרפוזיציה.
מודיפיקציה קלה של הניסוי (ראו בהמשך) מאפשרת את קבלת המצב
\(\displaystyle{ | \Psi\rangle = | u \rangle + | d \rangle
}\)
האם כשמסתכלים פונקצית הגל קורסת?
לפי פרשנות קופנהגן של תורת הקוונטים, חלקיק יכול להמצא במצב
סופרפוזיציה של מספר מצבי בסיס. כאשר מבצעים מדידה החלקיק "קורס"
לאחד ממצבי הבסיס. כאשר מנסים לדמיין מצב סופרפוזיציה בעולם המקרוסקופי
שבו אנו חיים, קשה לראות איך זה מתקיים, שכן לכאורה אין אנו רואים
תופעות כאלו בחיי היומיום. הניסוי המחשבתי ממחיש שאם המכניקה הקוונטית
נכונה בעולם המיקרוסקופי אזי היא (כנראה) נכונה גם בעולם
המקרוסקופי.
עובדה נסיונית: כאשר פותחים את הקופסא תמיד רואים חתול חי או חתול מת.
שאלה: האם הסופרפוזיציה "קורסת" כאשר מסתכלים עליה?
-
מצב של המוח לפני שפותחים את הקופסא:
\(\displaystyle{ |
\phi\rangle }\)
-
מצב של המוח אם רואים חתול חי:
\(\displaystyle{ | +\rangle }\)
-
מצב של המוח אם רואים חתול מת:
\(\displaystyle{ | -\rangle }\)
-
מצב היקום לפני שפותחים את הקופסא:
\(\displaystyle{ | \Psi\rangle =
| \uparrow,u ;\phi \rangle + | \downarrow,d ;\phi \rangle
}\)
-
מצב היקום לאחר שפותחים את הקופסא:
\(\displaystyle{ | \Psi\rangle = | \uparrow,u ;+ \rangle +
| \downarrow,d ;- \rangle }\)
מהסתכלות בביטוי זה ניתן לראות כי לעולם לא נוכל להגיע למצב שבו נוכל
לראות את החתול גם חי וגם מת. או שניפתח את הקופסא ונחיה בעולם בו אנו
רואים את החתול חי, או שנפתח את הקופסא ונחיה בעולם בו אנו רואים את
החתול מת. פועל יוצא מזה היא "אינטרפרטציית העולמות המרובים של
המכניקה הקוונטית". לפי אינטרפטציה זו כל פעם שמתרחשת אינטראקציה היקום
מתפצל למספר יקומים שונים, באשר בכל יקום מתקיימת "היסטוריה" אחרת.
לעניות דעתו של המרצה מדובר כאן בסמנטיקה ששייכת לתחום המטפיסיקה, עם
השלכות בתחום היצירה הקולנועית.
מודיפיקציה של הניסוי המחשבתי
בניסוי המקורי למעשה לא קיבלנו חתול בסופרפוזיציה. כל המערכת (כולל
האטום) היתה בסופרפוזיציה. אם רוצים שרק החתול יהיה בסופרפוזיציה זה
אפשרי. לשם כך נחליף את האטום בספין 1/2, או בקיוביט, ונכין אותו (על ידי סיבוב / הפעלת הדמרד) במצב
\(\displaystyle{ | \rightarrow\rangle }\) .
לאחר מכן נתזמןאינטראקציה עם מתקן ההרעלה (שזו למעשה פעולת CNOT).
למתקן יש סנסור שבודק את הקיטוב האנכי.
המתקן משחרר רעל אם הספין בכיוון
\(\displaystyle{ |\downarrow\rangle }\).
מצב המערכת יהיה בהתאם:
\(\displaystyle{ | \Psi\rangle \ \ = \ \ | \uparrow,u \rangle \ + \ | \downarrow,d \rangle }\)
עד לשלב זה אין הבדל ביחס לניסוי המקורי (למעט העובדה שמדובר בספין שיכול להסתובב, או לחילופין בקיוביט, ולא באטום שיכול לדעוך).
אבל עכשיו נוסיף שלב נוסף - נסובב פעם שנייה (פעולת הדמרד) את הספין. נקבל:
\(\displaystyle{ |\Psi\rangle
\ \ = \ \ \Big[ |\uparrow\rangle \ + \ | \downarrow \rangle \Big] \otimes |u\rangle \ + \ \Big[ |\uparrow\rangle \ - \ | \downarrow \rangle \Big] \otimes |d\rangle \\
\ \ = \ \ | \uparrow,u\rangle \ + \ | \downarrow,u\rangle \ + \ | \uparrow,d \rangle \ - \ | \downarrow,d \rangle \\
\ \ = \ \ | \uparrow\rangle \otimes \Big[ |u\rangle \ + \ | d \rangle \Big] \ + \ | \downarrow \rangle \otimes \Big[ | u\rangle \ - \ | d \rangle \Big] } \)
עכשיו נפתח את הקופסא ונמדוד את הספין בכיוון האנכי.
אם התסריט הוא כזה שראינו ספין מקוטב למעלה, אז הסופרפוזיציה "קורסת" כך שמצב של החתול הוא
\(\displaystyle{ | \psi\rangle \ \ = \ \ | u \rangle \ + \ | d \rangle }\)
זה אומר שהחתול נמצא בסופרפוזיציה של חיים ומוות.
אם התסריט הוא כזה שראינו ספין מקוטב למטה, אז הסופרפוזיציה "קורסת" כך שמצב של החתול הוא
\(\displaystyle{ | \psi\rangle \ \ = \ \ | u \rangle \ - \ | d \rangle }\)
שהוא גם מצב סופרפוזיציה של חיים ומוות, אבל עם פאזה יחסית שונה.
אופציונלית, אם כוללים את מכשיר המדידה בתאור של המערכת, אז המצב לאחר שמתבצעת המדידה הוא:
\( \displaystyle{ |\Psi\rangle \ \ = \ \ | \uparrow \rangle \otimes \Big[ |u\rangle \ + \ | d \rangle \Big] \otimes |+\rangle \ + \ | \downarrow \rangle \otimes \Big[ | u\rangle \ - \ | d \rangle \Big] \otimes |-\rangle }\)
ביטוי זה ממחיש שהמצב של החתול הוא רלטיבי למה שראה הצופה בלי צורך להשתמש במונח המטעה "קריסה".
מדוע "הסתכלות" הורסת את הסופרפוזיציה
כאשר "מסתכלים" על אלקטרון שעובר דרך שני סדקים הסופרפוזיציה
נהרסת. כדי להבין את התופעה נתיחס לגרסת "שטרן גרלך" של הניסוי.
מכינים אלקטרונים עם קיטוב \(\displaystyle{ | \rightarrow\rangle
}\) ומעבירים אותם דרך מכשיר שטרן גרלך שמוצב אנכית. בתוך המכשיר הספין
נע במסלול עילי (y=u) או תחתי (y=d) בהתאם לכיוון הקיטוב האנכי שלו. זה
אומר שהמצב של האלקטרון בתוך המכשיר מתואר על ידי
\(\displaystyle{ | \Psi\rangle \ \ = \ \ |
\uparrow,u \rangle \ + \ | \downarrow,d
\rangle }\)
כאשר החלקיק יוצר מהמכשיר אנו מקבלים חזרה תנועה לאורך y=0 והמצב
התחילי משתחזר
\(\displaystyle{ | \Psi\rangle \ \ = \ \ |
\uparrow,0 \rangle \ + \ | \downarrow,0
\rangle \ \ = \ \ | \rightarrow,0 \rangle }\)
אם מתעלמים מהקואורדינטה האנכית, אפשר לרשום שהמצב הסופי של החלקיק הוא
\(\displaystyle{ | \Psi\rangle \ \ = \ \ |\rightarrow \rangle }\)
אבל אם האלקטרון עושה אינטראקציה עם הסביבה, או לחילופין אם צופה מסתכל על התנועה של האלקטרון כמו בסעיף הקודם, אז המצב של המערכת, בזמן שהאלקטרון נע בתוך המכשיר, הוא
\(\displaystyle{ | \Psi\rangle \ \ = \ \ |
\uparrow,u,+\rangle \ + \ | \downarrow,d,-
\rangle }\)
כאשר האלקטרון יוצא מהמכשיר המצב של המערכת יהיה
\(\displaystyle{ | \Psi\rangle \ \ = \ \ |
\uparrow,0,+\rangle \ + \ | \downarrow,0,-\rangle }\)
אם מתעלמים מהקואורדינטה האנכית, אפשר לרשום שהמצב הסופי של החלקיק והצופה הוא
\(\displaystyle{ | \Psi\rangle \ \ = \ \ |\rightarrow,+\rangle \ + \ |\rightarrow,-\rangle \ + \ | \leftarrow,+\rangle \ - \ | \leftarrow,-\rangle
}\)
אנחנו רואים שכבר לא מתקבל המצב
\(\displaystyle{ |\rightarrow\rangle }\)
. כתוצאה מהאינטרקציה עם הסביבה יש עכשיו הסתברות שווה למדידת שני
כיווני הקיטוב. צריך להדגיש שמה שחשוב הוא לא "ההסתכלות" כשלעצמה, אלא
האינטראקציה שגרמה לכך שהסביבה נכנסה לקורלציה עם מצב החלקיק. במילים
אחרות: החלקיק השאיר את חותמו על הסביבה ולכן אין לו אפשרות להתאבך
בחזרה עם עצמו.
מיון פצצות בשיטת אליצור-ווידמן
נניח שיש לנו 100 פצצות. מתוכן 50 הן פצצות דמה. לפצצה אמיתית יש דטקטור שאם עובר דרכו פוטון, אז הפצצה מתפוצצת. לעומת זאת בפצצת דמה הדטקטור הוא פיקטיבי ולא קורה שום דבר. במילים אחרות אפשר להגיד שפצצה אמיתית מבצעת "מדידה" של מעבר חלקיק דרכה, ופצצת דמה לא מבצעת מדידה כזו. נשאלת השאלה האם אפשר למיין את הפצצות כך שיהיה לנו ארסנל של פצצות שכולן אמיתיות. במבט ראשון התשובה שלילית, כי אם בודקים פצצה אמיתית אז היא מתפוצצת. כך שאם נבדוק את כולן נישאר עם 50 פצצות דמה.
אבל המכניקה הקוונטית נותנת לנו אופציה להתגבר (חלקית) על הבעיה. בגרסא הרשמית של הניסוי המחשבתי משתמשים בפוטונים, אבל בשביל הפדגוגיה אנו נשתמש להלן באלקטרונים. מה שנעשה זה זה להשתמש בסטאפ של הניסוי שתואר בסעיף הקודם. את "הצופה" נחליף בפצצה. אנו נניח שהדטקטור של הפצצה ממוקם במסלול העילי של מכשיר השטרלן-גרלך. נסמן ב
\(\displaystyle{ |- \rangle }\)
את המצב של דטקטור (לא דמה) לפני שעובד דרכו האלקטרון.
נסמן ב
\(\displaystyle{ |+ \rangle }\)
את המצב של הדטקטור (לא דמה) אחרי שעובר דרכו האלקטרון (שזה אומר שהפצצה מתפוצצת).
אם מדובר בפצצת-דמה אז ברור שנקבל ביציאה אלקטרון עם ספין שמקוטב ימינה. אם קיבלנו ספין מקוטב שמאלה זה אומר שהתבצעה מדידה, זה אומר שהפצצה אמיתית. במקרה האחרון יש הסתברות של 50% שהפצצה האמיתית לא התפוצצה. כך שבשורה התחתונה יש לנו סיכוי טוב לזהות רבע מהפצצות האמיתיות בלי שהן תתפוצצנה. אם נפעיל שוב את הפרוצדורה על מה שנשאר (רקוקרסיבית), נגיע למסקנה שאפשר לארגן ארסנל שכולל כשליש מהפצצות האמיתיות. שאר הפצצות האמיתיות תתפוצצנה בשעת המדידה. על ידי מודיפיקציה קלה של הפרוטוקול אפשר להוריד את הסתברות הפיצוץ בכל איטרציה, לכן ידרשו יותר איטרציות כדי לגלות פצצות אמיתיות, אבל הרווח יהיה שנוכל לזהות 50% מהפצצות האמיתיות.
קיים פרוטוקול אחר (אפקט זנו קוונטי) שמאפשר (אסימפסטוטית) זיהוי של כל הפצצות האמיתיות, בלי לפוצץ אף אחת.
איך יודעים שהחתול היה במצב סופרפוזיציה
בניסוי שתואר לעיל (אלקטרון שעובר דרך מכשיר שטרן גרלך) יש שני שלבים.
שלב ראשון: "שלב פיצול האלומה", שלב שני: "שלב איחוי האלומה". את השלב
השני קשה לבצע מבחינה טכנית. אם מדובר בחתול אז תנועה במסלול העילי
אנלוגית לחתול חי, ותנועה במסלול התחתי אנלוגית לחתול מת. כדי
שהאנולגיה תהיה מושלמת אפשר להניח שהמסלול העילי הוא קו ישר (0=y=u).
בשלב הראשון, האינטראקציה בין הספין (האטום) לבין
קואורדינטת-המסלול (החתול) גורמת לכך שאם נסתכל נראה בהסתברות של 50%
את החלקיק במסלול התחתי (y=d חתול מת). אבל אם לא מסתכלים על
הקואורדינטה (החתול), אז אפשר לשקם את המצב התחילי של המערכת. זאת
האינדיקציה לכך שבשעת המעבר במכשיר יש סופרפוזיציה או לא. הבעיה הטכנית
בהדגמה הניסיונית היא הצורך לבצע "איחוי" של האלומה, מה שאנלוגי להקמת
החתול לתחיה. כמו כן ברור שלצורך הסטטיסטיקה צריך לחזור על הניסוי הרבה
פעמים (הרבה חתולים ימותו...).
כמובן שאם משתמשים במקום בחתול ברגיסטר של קיוביטים אז הניסוי הוא אפשרי.
הערה "סמנטית" לגבי ניסוי שזירה
המתמטיקה הבסיסית של השזירה שמתבצעת בניסוי המחשבתי שנקרא "החתול של שרדינגר" חוזרת על עצמה בספרות בכל מיני גרסאות. המטרה של הגרסאות השונות היא לשווק את "המוזרות" של המכניקה הקוונטית בדרכים שונות, למרות שמדובר כל הזמן בדיוק באותה עלילה. רק הדמויות מתחלפות... בעניני מדידה קוונטית אפשר לקרוא לחתול "צופה" או "פוינטר" (מינוח שמשתמשים בו כשמתייחסים לתורת המדידה של פון-נוימן). בסיפור של אליצור-ווידמן החתול הוא "פצצה". במיחשוב קוונטי האטום של שרדינגר הוא control qubit, והחתול הוא קיוביט אחר (או רגיסטר) שנמצא ביחידת העיבוד של המחשב. בניסויים שהכותרת שלהם היא quantum eraser האטום והחתול הם שני פוטונים שזורים. הפוטון שמשחק את התפקיד של החתול נקרא "סיגנל". האם הסיגנל נמצא במצב של סופרפוזיציה נקבע על ידי המדידה של הפוטון השני שנקרא בספרות "איידלר".

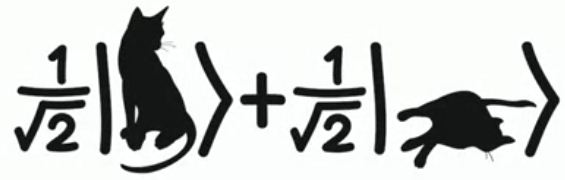 \(\displaystyle{ \Huge
\Psi \ = \ \ }\)
\(\displaystyle{ \Huge
\Psi \ = \ \ }\)