התאור המתמטי של גלים

מספרים קומפלקסים

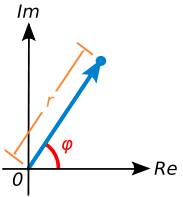
באנלוגיה למספרים "הממשיים" שמיצגים נקודות על "ציר המספרים", ניתן להתייחס אל מספר קומפלקסי כאל מייצג נקודה "במישור הקומפלקסי". אנו רושמים

\(\displaystyle{ z \ =\ (a,b) \ = \ a+ib \ = \ r e^{i\phi} }\)

צורת הכתיבה האחרונה קרויה "הצגה פולרית", באשר \(\displaystyle{ r }\) הוא גודלו של \(\displaystyle{ z }\) ובאשר \(\displaystyle{ \phi }\) היא הפאזה (זוית).

\(\displaystyle{ r \ \equiv \ \mid z\mid \ = \ \sqrt{a^2+b^2} }\)

\(\displaystyle{ a \ \ = \ \ r \ \cos(\phi) }\)
\(\displaystyle{ b \ \ = \ \ r \ \sin(\phi) }\)

מתנד

אוסצילטור הרמוני הוא לדוגמה "חלקיק קשור לקפיץ". התנועה שלו היא מחזורית ומאופינת בתדירות זויתית \(\displaystyle{ \omega }\) ובאמפליטודה \(\displaystyle{ A }\) . המצב של החלקיק בכל רגע ורגע מתואר על ידי המקום והמהירות שלו:

\(\displaystyle{ Q \ \ = \ \ A \ \cos(\phi_0 - \omega t) }\)
\(\displaystyle{ \dot{Q} \ \ = \ \ A\omega \ \sin(\phi_0 - \omega t) }\)

או לחילופין על ידי מספר קומפלקסי:

\(\displaystyle{ \psi \ \ = \ \ Q \ + \ i\frac{1}{\omega}\dot{Q} \ \ =\ \ Ae^{i\phi} }\)

באשר \(\displaystyle{ A }\) היא האמפליטודה, ובאשר \(\displaystyle{ \phi }\) היא הפאזה.
ההתפתחות של הפאזה בזמן היא

\(\displaystyle{ \phi(t) \ = \ \phi_0 - \omega t }\)

את התנועה של מתנד אפשר להמחיש כתנועה "בכיוון מחוגי השעון" על מעגל במישור הקומפלקסי. ההיטל של התנועה על הציר האופקי הוא ההעתק, וההיטל על הציר האנכי הוא המהירות.

גלים

אם המרחב כולל הרבה מתנדים, כל אחד יושב בנקודה אחרת, אז נרשום

\(\displaystyle{ \phi(x,t)= \phi_0(x) - \omega t }\)

במקרה של גל מישורי יש הפרש פאזה קבוע בין התנודות בנקודות סמוכות במרחב ובהתאם נרשום

\(\displaystyle{ \phi(x,t)= kx - \omega t }\)

\(\displaystyle{ \psi(x,t) \ \ = \ \ A e^{i( kx - \omega t)} }\)

\(\displaystyle{ \omega }\) היא התדירות הזוויתית ביחידות rad/sec
\(\displaystyle{ f=\omega/2\pi }\) היא התדירות ביחידות Hz
\(\displaystyle{ T=2\pi/\omega }\) הוא זמן המחזור.

\(\displaystyle{ k }\) הוא מספר הגל.
\(\displaystyle{ \lambda=2\pi/k }\) הוא אורך הגל.

בדרך כלל אם יוצרים הפרעה עם אורך גל מסוים אז תהיה לה תדירות מסוימת.
הקשר בין התדירות \(\displaystyle{ \omega }\) לבין \(\displaystyle{ k }\) נקרא יחס דיספרסיה. לגלי אור ולגלי קול יש יחס דיספרסיה לינארי:

\(\displaystyle{ \omega \ \ = \ \ c \ \mid k\mid }\)

בסעיף הבא נראה שמקדם הפרופורציה \(\displaystyle{ c }\) הוא המהירות של התקדמות הפרעה.

חבילת גלים (wave-packet)

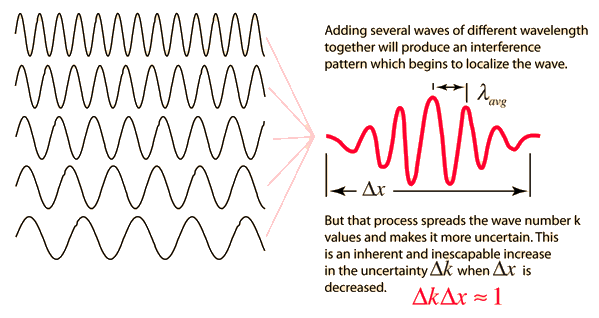
כאשר פורטים על מיתר, לא יוצרים גל מישורי, אלא "חבילת גלים" ממוקמת מבחינה מרחבית.
ככל שהחבילה ממוקמת יותר ( \(\displaystyle{ \Delta x }\) קטן) , אורך הגל שלה הופך להיות פחות מוגדר ( \(\displaystyle{ \Delta k }\) גדול).
לאחר זמן מסוים החבילה "נמרחת" על כל המיתר (spreading of wave-packet).

\(\displaystyle{ \psi(x,t) \ \ = \ \sum_k \ A_k e^{i( kx - \omega_k t)} }\)

עבור חבילת גלים עם יחס דיספרסיה לינארי אפשר לרשום את הביטוי לעיל בצורה

\(\displaystyle{ \psi(x,t) \ \ = \ \ f(x-ct) }\)

יחס דיספרסיה לא לינארי

לא תמיד יחס הדיספרסיה הוא לינארי. נניח שיש לנו כדורים קשורים בקפיצים (ציור למעלה) ושבנוסף מעגנים את הכדורים לציר המרכזי באמצעות קפיצים נוספים. במקרה כזה הקשר בין תדירות התנודה לאורך הגל יהיה

\(\displaystyle{ \omega \ \ = \ \ \sqrt{ \omega_0^2 \ + \ (c k)^2} }\)

אם אורך הגל ארוך מאוד אז אפשר להתעלם מהקפיצים שמחברים את הכדורים ומקבלים \(\displaystyle{ \omega = \omega_0 }\) . אם אורך הגל קצר מאוד אפשר להתעלם מהקפיצים המעגנים ומקבלים יחס דיספרסיה לינארי. את המהירות של חבילת גלים אפשר לחשב מתוך כך שמקרבים את התלות של התדירות במספר הגל על-ידי יחס לינארי. מכך משתמע שמהירות התנועה של החבילה תהיה

\(\displaystyle{ v \ \ = \ \ \frac{d\omega}{d k} \ \ \text{[calculated for the average wavenumber]} }\)