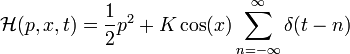
The kicked rotator

[variation of the wiki that I have placed in Wikipedia]

The Kicked Rotator is a prototype model for chaos and quantum chaos studies. It describes a particle that is free to move on a ring (equivalently: a stick that is free to rotate). The particle is kicked periodically by an homogeneous field (equivalently: the gravitation is switched on periodically in short pulses). The model is described by the Hamiltonian

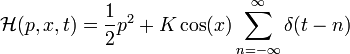
\mathcal{H}(p,x,t)= \frac{1}{2}p^2 + K \cos(x) \sum_{n=-\infty}^{\infty} \delta(t-n)
and its dynamics is described by the standard map. See more details and references there, or better in the associated Scholarpedia entry. In the classical analysis, if the kicks are strong enough, there is a diffusion in energy space

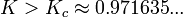
K>K_c\approx0.971635...
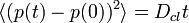
\langle (p(t)-p(0))^2 \rangle = D_{cl} t
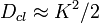
D_{cl}\approx K^2/2
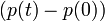The quasi-random approximation for the diffusion coefficient that is cited above is implied by the observation that the change (p(t)-p(0)) in the momentum is the sum of quasi-random kicks 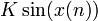K\sin(x(n)). In the quantum analysis the propagation is realized by iterations with the unitary operator

\hat{U} = \exp\left[-i\frac{1}{2\hbar}\hat{p}^2\right] \exp\left[-i\frac{1}{\hbar} K\cos\hat{x}\right]


It has been discovered [1] that the classical diffusion is suppressed, and later it has been understood [2] that this is a manifestation of a quantum dynamical localization effect that parallels Anderson Localization. There is a general argument [3] that leads to the following estimate for the breaktime of the diffusive behavior

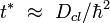
t^* \ \approx \ D_{cl}/\hbar^2

The associated localization scale in momentum is therefore 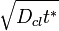\sqrt{D_{cl} t^*}.


The effect of noise and dissipation

If noise is added to the system, the dynamical localization is destroyed, and diffusion is induced[4][5]. This is somewhat similar to hopping conductance. The proper analysis requires to figure out how the dynamical correlations that are responsible for the localization effect are diminished.


Recall that an exact expression for 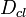D_{cl} is obtained in the classical analysis by calculating the "area" of the correlation function

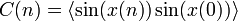
C(n) = \langle \sin(x(n))\sin(x(0)) \rangle

namely

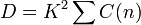
D = K^2\sum C(n)

Note that 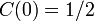C(0)=1/2. Neglectiong all other correlations, it leads to the quasi-random approximation. The same calculation recipe holds also in the quantum mechanical case, and also if noise is added.  In the quantum case, without noise, the area under 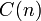C(n) is zero (due to long negative tails), while with noise a practical approximation is

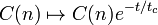
C(n)\mapsto C(n) e^{-t/t_c}

where the coherence time 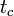t_c is inversely proportional to the intensity of the noise. Consequently the noise induced diffusion coefficient is

D \approx D_{cl}t^* / t_c \quad [\text{assuming }t_c \gg t^*]


Also the problem of quantum kicked rotator with dissipation (due to coupling to a thermal bath) has been considered. There is an issue here how to introduce an interaction that respects the angle periodicity of the position 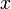x coordinate, and is still spatially homogeneous. In the first works [6] a quantum-optic type interaction has been assumed that involves a momentum dependent coupling. Later[7] a way to formulate a purely position dependent coupling, as in the Calderia-Leggett model, has been figured out, which can be regarded as the earlier version of the DLD model.

Experiments

Experimental realizations of the quantum kicked rotator have been achieved by the Austin group[8], and by the Auckland group[9], and have encouraged a renewed interest in the theoretical analysis: for further reference see [10].

References

  1. G. Casati, B.V. Chirikov, F.M. Izrailev and J. Ford, in Stochastic Behaviour in classical and Quantum Hamiltonian Systems, Vol. 93 of Lecture Notes in Physics, edited by G. Casati and J. Ford (Springer, N.Y. 1979), p. 334
  2. S. Fishman, D.R. Grempel and R.E. Prange, Phys. Rev. Lett. 49, 509 (1982). D.R. Grempel, R.E. Prange and S. Fishman, Phys. Rev. A 29, 1639 (1984). S. Fishman, R.E. Prange, M. Griniasty, Phys. Rev. A 39, 1628 (1989). S. Fishman, D.R. Grempel and R.E. Prange, Phys. Rev. A 36, 289 (1987).
  3. B.V. Chirikov, F.M. Izrailev and D.L. Shepelyansky, Sov. Sci. Rev. 2C, 209 (1981). D.L. Shepelyansky, Physica 28D, 103 (1987).
  4. E. Ott, T.M. Antonsen Jr. and J.D. Hanson, Phys. Rev. Lett. 53, 2187 (1984).
  5. D. Cohen, Phys. Rev. A 44, 2292 (1991); Phys. Rev. Lett. 67, 1945 (1991); http://arxiv.org/abs/chao-dyn/9909016
  6. T. Dittrich and R. Graham, Z. Phys. B 62, 515 (1986); Ann. Phys. {\bf 200}, 363 (1990).
  7. D. Cohen, J. Phys. A 27, 4805 (1994)
  8. Klappauf, Oskay, Steck and Raizen, Phys. Rev. Lett. 81, 1203 (1998)
  9. Ammann, Gray, Shvarchuck and Christensen, Phys. Rev. Lett. 80, 4111 (1998)
  10. M. Raizen in New directions in quantum chaos, Proceedings of the International School of Physics Enrico Fermi, Course CXLIII, Edited by G. Casati, I. Guarneri and U. Smilansky (IOS Press, Amsterdam 2000).